《2025年初中必刷题八年级数学上册华师大版》

1 [2024河南平顶山期中,中]小明在爬一小山时,第一阶段的平均速度为$2v$,所用时间为$t_{1}$;第二阶段的平均速度为$v$,所用时间为$t_{2}$.下山时,小明的平均速度保持为$4v$.已知小明上山的路程和下山的路程是相同的,那么小明下山用时为 ( )

A.$2t_{1}+4t_{2}$
B.$\frac {1}{2}t_{1}+4t_{2}$
C.$2t_{1}+\frac {1}{4}t_{2}$
D.$\frac {1}{2}t_{1}+\frac {1}{4}t_{2}$

答案： D【解析】
∵小明上山时,第一阶段的平均速度为2v,所用时间为$t_{1}$;第二阶段的平均速度为v,所用时间为$t_{2}$,
∴总路程为$2vt_{1}+vt_{2}$.
∵小明上山的路程和下山的路程是相同的,
∴小明下山用时为$(2vt_{1}+vt_{2})÷4v=\frac {1}{2}t_{1}+\frac {1}{4}t_{2}$.故选D.

2 [中]已知$(12a^{3}-6a^{2}+3a)÷3a-2a= 0且b= 2$,则式子$(\frac {2}{3}ab^{2}-2ab)\cdot \frac {1}{2}ab$的值为 ____.

答案： $-\frac {1}{3}$【解析】$\because (12a^{3}-6a^{2}+3a)÷3a-2a=0,\therefore 4a^{2}-2a+1-2a=0,\therefore (2a-1)^{2}=0$,解得$a=\frac {1}{2}.\because (\frac {2}{3}ab^{2}-2ab)\cdot \frac {1}{2}ab=\frac {1}{3}a^{2}b^{3}-a^{2}b^{2}$,
∴把$a=\frac {1}{2},b=2$代入,得原式$=\frac {1}{3}×(\frac {1}{2})^{2}×2^{3}-(\frac {1}{2})^{2}×2^{2}=\frac {2}{3}-1=-\frac {1}{3}$.故答案为$-\frac {1}{3}.$

3 [2025四川宜宾期末,中]如图,窗框由一个长方形和一个半圆组成,若要把窗框形状设计成一个新的长方形,面积保持不变,且底边长仍为$a$,则高度应为 ____.

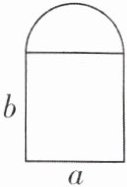
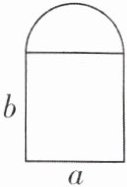
答案： $b+\frac {1}{8}πa$【解析】设新长方形的高度为x.原面积为$ab+\frac {1}{2}π\cdot (\frac {a}{2})^{2}$.
∵面积保持不变,$\therefore ab+\frac {1}{2}π\cdot (\frac {a}{2})^{2}=ax,\therefore x=[ab+\frac {1}{2}π\cdot (\frac {a}{2})^{2}]÷a=(ab+\frac {1}{8}πa^{2})÷a=b+\frac {1}{8}πa$.故答案为$b+\frac {1}{8}πa.$

4 新考法[2025河南周口期中,中]小明在做练习册上的一道多项式除以单项式的习题时,一不小心弄污了这道习题,被污渍盖住后的习题形式如下:$(● -3x^{2}y)÷●$.小明翻看了书后的正确答案是“$4x^{2}y^{2}-3xy+6x$”,复原这道习题为 ____.

答案： $(-2x^{3}y^{3}+\frac {3}{2}x^{2}y^{2}-3x^{2}y)÷(-\frac {1}{2}xy)$或$(4x^{3}y^{2}+6x^{2}-3x^{2}y)÷x$【解析】由题意得,有两种情况:①除式是$-3x^{2}y÷6x=-\frac {1}{2}xy$,此时被除式是$(4x^{2}y^{2}-3xy+6x)\cdot (-\frac {1}{2}xy)=-2x^{3}y^{3}+\frac {3}{2}x^{2}y^{2}-3x^{2}y$,
∴这道习题为$(-2x^{3}y^{3}+\frac {3}{2}x^{2}y^{2}-3x^{2}y)÷(-\frac {1}{2}xy)$;②除式是$-3x^{2}y÷(-3xy)=x$,此时被除式是$(4x^{2}y^{2}-3xy+6x)\cdot x=4x^{3}y^{2}-3x^{2}y+6x^{2}$,
∴这道习题为$(4x^{3}y^{2}+6x^{2}-3x^{2}y)÷x$.综上所述,这道习题为$(-2x^{3}y^{3}+\frac {3}{2}x^{2}y^{2}-3x^{2}y)÷(-\frac {1}{2}xy)$或$(4x^{3}y^{2}+6x^{2}-3x^{2}y)÷x.$

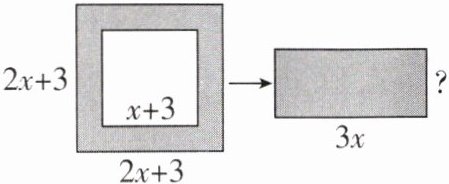
5 [2024河北石家庄长安区模拟,中]如图,在边长为$2x+3的正方形纸片中剪下一个边长为x+3$的正方形,剩余部分(即阴影部分)可剪拼成一个长方形,若拼成的长方形一边长为$3x$,求另一边的长.

答案： 【解】$[(2x+3)^{2}-(x+3)^{2}]÷3x=[(4x^{2}+12x+9)-(x^{2}+6x+9)]÷3x=(3x^{2}+6x)÷3x=x+2$,则拼成的长方形另一边的长为$x+2.$

6 核心素养运算能力[较难]我们已经学习过多项式除以单项式的计算方法,多项式除以多项式一般可用竖式计算,例如:计算(6x^{4}-7x^{3}-x^{2}-1)÷(2x+1),可用竖式计算如下:
$\begin{array}{r}3x^{3}-5x^{2}+2x-1 \\\hline2x+1\enclose{longdiv}{6x^{4}-7x^{3}-x^{2}+0\cdot x-1} \\6x^{4}+3x^{3} \\\hline-10x^{3}-x^{2} \\-10x^{3}-5x^{2} \\\hline4x^{2}+0\cdot x \\4x^{2}+2x \\\hline-2x-1 \\-2x-1 \\\hline0\end{array} $所以6x^{4}-7x^{3}-x^{2}-1除以2x+1,商式为3x^{3}-5x^{2}+2x-1,余式为0.据此回答下列问题:(1)(x^{3}-x^{2}-4x+4)÷(x-2)= ____;(2)(x^{2}+2x+4)÷(x-1),余式为 ____;(3)若x^{3}+ax^{2}+bx-2能被x^{2}+2x+2整除,求a,b的值.

答案：
(1)$x^{2}+x-2$
(2)7
(3)【解】设商式为$(x+m)$,则有$x^{3}+ax^{2}+bx-2=(x+m)(x^{2}+2x+2)=x^{3}+(2+m)x^{2}+(2+2m)x+2m$,所以$-2=2m$,所以$m=-1$,所以$a=2+m=1,b=2+2m=0$.所以$a=1,b=0.$