第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2024河南新乡卫滨区校级期末]如图,在Rt△ABC中,∠B= 90°,AB= 6,AC= 10,以边BC为直径作一个半圆,则半圆(阴影部分)的面积为( )
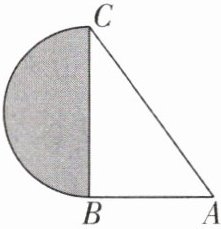
A.4π
B.8π
C.12π
D.16π

A.4π
B.8π
C.12π
D.16π
答案:
B [解析]
∵∠B=90°,AB=6,AC=10,
∴BC= $\sqrt{AC²−AB²}$=$\sqrt{10²−6²}$=8,
∴阴影部分的面积为$\frac{1}{2}$×π×4²=8π.故选B.
∵∠B=90°,AB=6,AC=10,
∴BC= $\sqrt{AC²−AB²}$=$\sqrt{10²−6²}$=8,
∴阴影部分的面积为$\frac{1}{2}$×π×4²=8π.故选B.
2 [2025安徽合肥期末]如图所示,在数轴上,点B,C所表示的数分别是-1,1,CD垂直于数轴,且CD= 1,以B为圆心,BD长为半径画弧,交数轴于点A(在点B左侧),若点A所表示的数为a,则a的值为( )
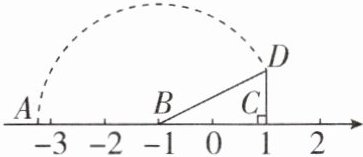
A.-√5
B.-1 - √5
C.1 - √5
D.-1 + √5

A.-√5
B.-1 - √5
C.1 - √5
D.-1 + √5
答案:
B [解析]由题意得BC=2,CD=1,
∴由勾股定理得BD= $\sqrt{2²+1²}$=$\sqrt{5}$,
∴BA=BD=$\sqrt{5}$,
∴a= - 1 - $\sqrt{5}$.故选B.
∴由勾股定理得BD= $\sqrt{2²+1²}$=$\sqrt{5}$,
∴BA=BD=$\sqrt{5}$,
∴a= - 1 - $\sqrt{5}$.故选B.
3 已知Rt△ABC的两直角边长分别是6cm,8cm,则Rt△ABC的斜边上的高是( )
A.4.8cm
B.2.4cm
C.48cm
D.10cm
A.4.8cm
B.2.4cm
C.48cm
D.10cm
答案:
A [解析]设Rt△ABC斜边上的高为h cm.
∵Rt△ABC的两直角边长分别是6 cm,8 cm,
∴斜边长为 $\sqrt{6²+8²}$=10(cm).
∵$\frac{1}{2}$×10×h = $\frac{1}{2}$×6×8,
∴h = 4.8,即Rt△ABC的斜边上的高是4.8 cm,故选A.
∵Rt△ABC的两直角边长分别是6 cm,8 cm,
∴斜边长为 $\sqrt{6²+8²}$=10(cm).
∵$\frac{1}{2}$×10×h = $\frac{1}{2}$×6×8,
∴h = 4.8,即Rt△ABC的斜边上的高是4.8 cm,故选A.
4 [2025四川宜宾期中]直角三角形两条直角边长之和为3.5,面积为1.5,则斜边长为______。
答案:
2.5 [解析]设一条直角边长为a,另一条直角边长为b,斜边长为c.由题意可得a + b = 3.5,$\frac{1}{2}$ab = 1.5,
∴ab = 3,
∴c² = a² + b² = (a + b)² - 2ab = (3.5)² - 2×3 = 6.25.
∵c>0,
∴c = 2.5,故答案为2.5.
∴ab = 3,
∴c² = a² + b² = (a + b)² - 2ab = (3.5)² - 2×3 = 6.25.
∵c>0,
∴c = 2.5,故答案为2.5.
5 [2024山东威海文登区期中]如图,在△ABC中,∠A= 90°,BE是△ABC的角平分线,ED⊥BC于点D,BC= 5,AB= 3,则DE的长是______。
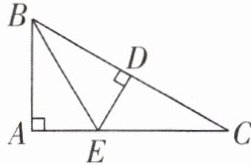

答案:
$\frac{3}{2}$ [解析]在△ABC中,∠A = 90°,BC = 5,AB = 3,则AC = $\sqrt{BC²−AB²}$ = $\sqrt{5²−3²}$ = 4.
∵BE是△ABC的角平分线,ED⊥BC,∠A = 90°,
∴AE = DE.
∵S△ABC = S△BAE + S△BCE,
∴$\frac{1}{2}$×3×4 = $\frac{1}{2}$×3×DE + $\frac{1}{2}$×5×DE,解得DE = $\frac{3}{2}$,故答案为$\frac{3}{2}$.
∵BE是△ABC的角平分线,ED⊥BC,∠A = 90°,
∴AE = DE.
∵S△ABC = S△BAE + S△BCE,
∴$\frac{1}{2}$×3×4 = $\frac{1}{2}$×3×DE + $\frac{1}{2}$×5×DE,解得DE = $\frac{3}{2}$,故答案为$\frac{3}{2}$.
6 [2025河南驻马店泌阳期末]周末,小明和小亮去碧沙岗公园放风筝,如图,为了测得风筝的垂直高度CE,他们进行了测量,得到如下数据:①牵线放风筝的小明的身高为1.65米;②风筝与小明的水平距离BD的长为12米;③根据手中剩余线的长度计算出风筝线BC的长为20米。
(1)求风筝的垂直高度CE;
(2)要使风筝沿CD方向下降7米,则小明应该往回收风筝线多少米?
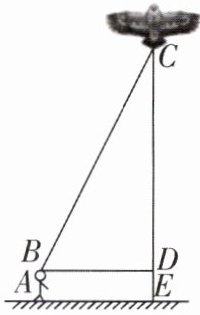
(1)求风筝的垂直高度CE;
(2)要使风筝沿CD方向下降7米,则小明应该往回收风筝线多少米?

答案:
[解]
(1)由题意可知BD = 12米,BC = 20米,CD⊥BD,AB = DE = 1.65米.在Rt△CDB中,由勾股定理得,CD² = BC² - BD² = 20² - 12² = 256,
∴CD = 16米(负值已舍去),
∴CE = CD + DE = 16 + 1.65 = 17.65(米).答:风筝的垂直高度CE为17.65米.
(2)如图,风筝沿CD方向下降7米至C'处,DE保持不变,连结BC',此时C'D = 16 - 7 = 9(米).在Rt△C'DB中,BD = 12米,
∴BC' = $\sqrt{C'D²+BD²}$ = $\sqrt{9²+12²}$ = 15(米),
∴小明应该往回收风筝线20 - 15 = 5(米).

[解]
(1)由题意可知BD = 12米,BC = 20米,CD⊥BD,AB = DE = 1.65米.在Rt△CDB中,由勾股定理得,CD² = BC² - BD² = 20² - 12² = 256,
∴CD = 16米(负值已舍去),
∴CE = CD + DE = 16 + 1.65 = 17.65(米).答:风筝的垂直高度CE为17.65米.
(2)如图,风筝沿CD方向下降7米至C'处,DE保持不变,连结BC',此时C'D = 16 - 7 = 9(米).在Rt△C'DB中,BD = 12米,
∴BC' = $\sqrt{C'D²+BD²}$ = $\sqrt{9²+12²}$ = 15(米),
∴小明应该往回收风筝线20 - 15 = 5(米).

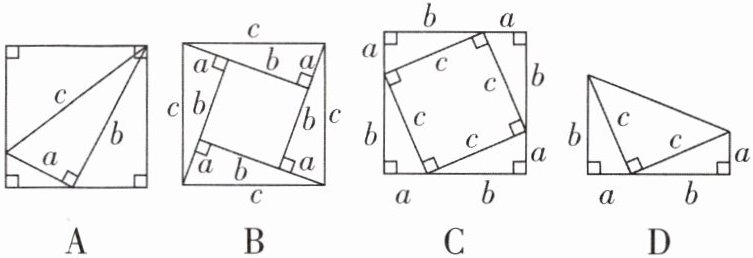
7 [2024山东淄博临淄区期中]若a,b为直角三角形的两直角边,c为斜边,则下列选项中不能用来证明勾股定理的是( )

答案:
A [解析]选项A不能用来证明勾股定理,故符合题意;选项B,大正方形的面积为4×$\frac{1}{2}$ab + (b - a)² = 2ab + a² + b² - 2ab = a² + b² = c²,能证明勾股定理,不符合题意;选项C,大正方形的面积为(a + b)² = 4×$\frac{1}{2}$ab + c²,化简得a² + b² = c²,能证明勾股定理,不符合题意;选项D,梯形的面积为$\frac{1}{2}$(a + b)(a + b) = 2×$\frac{1}{2}$ab + $\frac{1}{2}$c²,化简得a² + b² = c²,能证明勾股定理,不符合题意.故选A.
8 若直角三角形的两边长分别为a,b,且满足$(a - 3)^2 + $|b - 4| = 0,则该直角三角形的第三边长的平方为______。
答案:
25或7 [解析]
∵(a - 3)² + |b - 4| = 0,
∴a - 3 = 0,b - 4 = 0,
∴a = 3,b = 4.当b = 4为直角边长时,第三边长的平方为3² + 4² = 25;当b = 4为斜边长时,第三边长的平方为4² - 3² = 7.故答案为25或7.
∵(a - 3)² + |b - 4| = 0,
∴a - 3 = 0,b - 4 = 0,
∴a = 3,b = 4.当b = 4为直角边长时,第三边长的平方为3² + 4² = 25;当b = 4为斜边长时,第三边长的平方为4² - 3² = 7.故答案为25或7.
查看更多完整答案,请扫码查看


