《2025年初中必刷题八年级数学上册华师大版》

1[2025陕西渭南期末,中]如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,连结AO. 如果AB= AC,那么图中全等的直角三角形的对数是( )

A.1
B.2
C.3
D.4

答案： C 【解析】
∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°. 在△ADC 和△AEB 中，{∠ADC=∠AEB,∠DAC=∠EAB,AC=AB},
∴△ADC≌△AEB(AAS),
∴AD=AE,∠C=∠B.
∵AB=AC,
∴BD=CE. 在△BOD 和△COE 中，{∠B=∠C,∠BOD=∠COE,BD=CE},
∴△BOD≌△COE(AAS),
∴OD=OE. 在 Rt△ADO 和 Rt△AEO 中，{OA=OA,OD=OE},
∴ Rt△ADO≌Rt△AEO(HL).
∴共有 3 对全等的直角三角形，故选 C.

2[2024重庆渝中区校级期末,中]如图,△ABC中,BD⊥AC于点D,E为AC边上一点,连结BE并延长至F,使BF= BC,连结AF,∠CBF= ∠FAC,若AC= 7.4,AF= 5.2,则AD的长度为______.

答案：
1.1 【解析】如图，过点 B 作 BG⊥FA 交 FA 的延长线于点 G.
∵∠CBF=∠FAC,∠BEC=∠AEF,
∴∠C=∠F.
∵BD⊥AC,BG⊥FA,
∴∠BDC=∠BGF=90°. 在△BCD 和△BFG 中，{∠BDC=∠BGF,∠C=∠F,BC=BF},
∴△BCD≌△BFG(AAS),
∴CD=FG,BD=BG. 在 Rt△BAD 和 Rt△BAG 中，{AB=AB,BD=BG},
∴ Rt△BAD≌Rt△BAG(HL),
∴AD=AG.
∵CD=FG,
∴CD=AF+AG=AF+AD,
∴AC+AF=2CD,
∴CD=$\frac{7.4 + 5.2}{2}$=6.3,
∴AD=AC - CD=7.4 - 6.3=1.1. 故答案为 1.1.

3[中]如图,∠C= 90°,AC= 20,BC= 10,AX⊥AC,垂足为A,点P和点Q同时从点A出发,分别在线段AC和射线AX上运动,且AB= PQ,当AP= ______时,以点A,P,Q为顶点的三角形与△ABC全等.

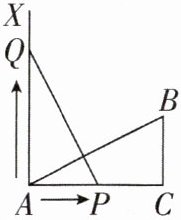
答案： 10 或 20 【解析】
∵AX⊥AC,
∴∠PAQ=90°,
∴∠C=∠PAQ=90°. 分两种情况：①当 AP=BC=10 时，在 Rt△ABC 和 Rt△QPA 中，{AB=PQ,BC=AP},
∴ Rt△ABC≌Rt△QPA(HL);②当 AP=CA=20 时，在 Rt△ABC 和 Rt△PQA 中，{AB=PQ,AC=AP},
∴ Rt△ABC≌Rt△PQA(HL). 综上所述，当 AP=10 或 20 时，△ABC 与以 A,P,Q 为顶点的三角形全等. 故答案为 10 或 20.

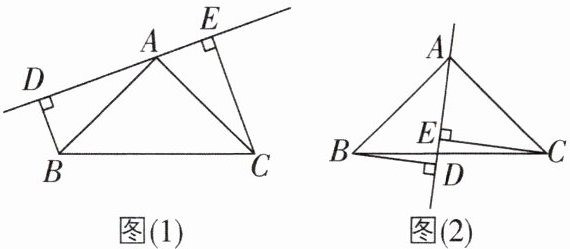
4[较难]在△ABC中,AB= AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)若B,C在DE的同侧(如图(1)所示),且AD= CE,求证：AB⊥AC.
(2)若B,C在DE的两侧(如图(2)所示),且AD= CE,其他条件不变,AB与AC仍垂直吗？若垂直,请给出证明；若不垂直,请说明理由.

答案： （1）【证明】
∵BD⊥DE 于点 D,CE⊥DE 于点 E,
∴∠ADB=∠AEC=90°. 在 Rt△ABD 和 Rt△CAE 中，{AB=CA,AD=CE},
∴ Rt△ABD≌Rt△CAE(HL),
∴∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,
∴∠DAB+∠EAC=90°,
∴∠BAC=180° - (∠DAB+∠EAC)=90°,
∴AB⊥AC.
（2）【解】AB⊥AC. 证明如下：同（1）可证 Rt△ABD≌Rt△CAE,
∴∠DAB=∠ECA.
∵∠CAE+∠ECA=90°,
∴∠CAE+∠DAB=90°，即∠BAC=90°,
∴AB⊥AC.

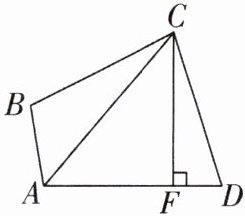
5[较难]如图,四边形ABCD中,AC为∠BAD的平分线,过点C作CF⊥AD,已知CB= CD.
(1)判断∠ABC与∠ADC之间的数量关系；
(2)若CF= 6,AB= 4,S△ACD= 21,求DF的长.

答案：
【解】（1）∠ABC+∠ADC=180°. 理由如下：如图，过点 C 作 CH⊥AB，交 AB 的延长线于 H.
∵AC 平分∠BAD,
∴∠BAC=∠CAD. 在△ACH 和△ACF 中，{∠BAC=∠CAD,∠H=∠AFC=90°,AC=AC},
∴△ACH≌△ACF(AAS),
∴CH=CF,AH=AF. 在 Rt△BCH 和 Rt△DCF 中，{CB=CD,CH=CF},
∴ Rt△BCH≌Rt△DCF(HL),
∴∠ADC=∠CBH.
∵∠CBH+∠ABC=180°,
∴∠ADC+∠ABC=180°.
（2）
∵ Rt△BCH≌Rt△DCF,
∴BH=DF.
∵S△ACD=$\frac{1}{2}$×AD×CF=21,CF=6,
∴AD=7.
∵AD+AB=AF+FD+AH - BH=2AF=7+4=11,
∴AF=$\frac{11}{2}$,
∴DF=AD - AF=1.5.

6[较难]如图(1),E,F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB= CD,AF= CE,BD交AC于点M.
(1)求证：MB= MD,ME= MF.
(2)当E,F两点移动到如图(2)的位置时,其余条件不变,上述结论能否成立？若成立,请给予证明；若不成立,请说明理由.

答案： （1）【证明】
∵DE⊥AC 于 E,BF⊥AC 于 F,
∴∠DEC=∠BFA=90°. 在 Rt△DEC 和 Rt△BFA 中，
∵{CD=AB,CE=AF},
∴ Rt△DEC≌Rt△BFA(HL),
∴DE=BF. 在△DEM 和△BFM 中，
∵{∠DME=∠BMF,∠DEM=∠BFM,DE=BF},
∴△DEM≌△BFM(AAS),
∴MB=MD,ME=MF.
（2）【解】成立. 证明：
∵DE⊥AC 于 E,BF⊥AC 于 F,
∴∠DEC=∠BFA=90°. 在 Rt△DEC 和 Rt△BFA 中，
∵{CD=AB,CE=AF},
∴ Rt△DEC≌Rt△BFA(HL),
∴DE=BF. 在△DEM 和△BFM 中，
∵{∠DME=∠BMF,∠DEM=∠BFM,DE=BF},
∴△DEM≌△BFM(AAS),
∴MB=MD,ME=MF.