《2025年初中必刷题八年级数学上册华师大版》

1 [2024 山西运城期末] 如图，$l_{1}// l_{2}$，等边三角形 ABC 的顶点 B，C 分别在$l_{1}$，$l_{2}$上，若$∠1 = 20^{\circ}$，则$∠2$的大小为 （ ）

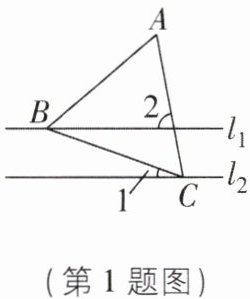
A.$65^{\circ}$
B.$70^{\circ}$
C.$80^{\circ}$
D.$85^{\circ}$

答案： C

2 [2025 福建龙岩期末] 如图，在等边三角形 ABC 中，$BD⊥AC$，$BF = BD$，则$∠CDF$的度数是 （ ）

A.$10^{\circ}$
B.$15^{\circ}$
C.$20^{\circ}$
D.$25^{\circ}$

答案： B

3 如图，等边三角形 ABC 中，AD 是 BC 上的高，$∠BDE = ∠CDF = 60^{\circ}$，图中与 BD 相等的线段有 （ ）

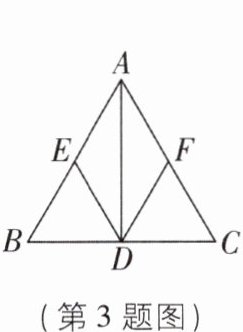
A.5 条
B.6 条
C.7 条
D.8 条

答案： C

4 新考法 [2025 浙江金华期中] 如图，$\triangle ABC$是等边三角形，D 是线段 BC 上一动点（不与点 B，C 重合），连结 AD，点 E，F 分别在线段 AB，AC 的延长线上，连结 DE，DF，且$DE = DF = AD$，在点 D 从 B 运动到 C 的过程中，$\triangle BED$周长的变化规律是 （ ）

A.先变大后变小
B.不变
C.先变小后变大
D.一直变小

答案： C

5 [2025 山东泰安质检] 如图，已知等边三角形纸片 ABC，点 E 在 AC 边上，点 F 在 AB 边上，将纸片沿 EF 折叠，使点 A 落在 BC 边上的点 D 处，且$ED⊥BC$，则$∠EFD = $______。

答案： 45°

6 如图所示，$\triangle ABC$是等边三角形，且$BD = CE$，$∠1 = 15^{\circ}$，则$∠2$的度数为______。

答案： 60°

7 如图，已知等边三角形 ABC 的高为 7 cm，P 为$\triangle ABC$内一点，$PD⊥AB$于点 D，$PE⊥AC$于点 E，$PF⊥BC$于点 F，则$PD + PE + PF = $______。

答案： 7cm

8 如图，$\triangle ABC$是等边三角形，BD 是中线，延长 BC 到点 E，使$CE = CD$，连结 DE，则 DB 和 DE 是否相等？为什么？

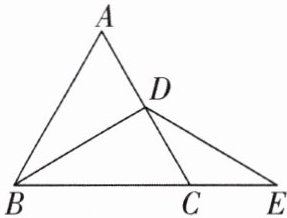
答案： DB=DE.理由:如图,过D作DG⊥BE于G.
∵△ABC是等边三角形,BD是中线，
∴∠ABC=∠ACB=60°,∠DBC=30°(等腰三角形“三线合一”).又
∵CE=CD,
∴∠CDE=∠CED.又
∵∠ACB=∠CDE+∠CED,
∴ ∠CDE=∠CED=1/2∠BCD=30°,
∴∠DBC=∠DEC.在△BDG和△EDG中,{∠DGB=∠DGE=90°,∠DBG=∠DEG,DG=DG,}
∴△BDG≌△EDG(AAS),
∴DB=DE.

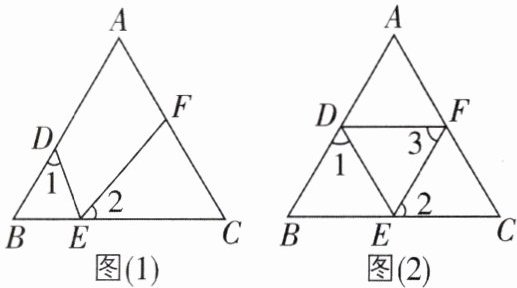
9 如图，$\triangle ABC$是等边三角形，D，E，F 分别是 AB，BC，AC 上一点，且$∠DEF = 60^{\circ}$。
（1）如图（1），若$∠1 = 50^{\circ}$，求$∠2$的度数；
（2）如图（2），连结 DF，若$DF// BC$，求证：$∠1 = ∠3$。

答案：
(1)[解]
∵△ABC是等边三角形,
∴∠B=∠A=∠C=60°.
∵∠B+∠1+∠DEB=180°,∠DEB+∠DEF+∠2=180°,∠DEF=60°,
∴∠1+∠DEB=∠2+∠DEB,
∴∠2=∠1=50°.
(2)[证明]
∵DF//BC,
∴∠FDE=∠DEB.
∵∠B+∠1+∠DEB=180°,∠FDE+∠3+∠DEF=180°,∠B=60°,∠DEF=60°,
∴∠1=∠3.