第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [中]如图,AD 是△ABC 的中线,点 E 在 BC 的延长线上,CE = AB,∠BAC = ∠BCA,试说明:AE = 2AD。


答案:
如图,延长AD至M,使DM=AD.因为AD是△ABC的中线,所以BD=CD.在△ABD和△MCD中,$\left\{\begin{array}{l} BD=CD,\\ ∠ADB=∠MDC,\\ AD=MD,\end{array}\right. $所以△ABD≌△MCD(SAS),所以MC=AB,∠B=∠MCD.因为AB=CE,所以CM=CE.因为∠BAC=∠BCA,所以∠B+∠BAC=∠ACB+∠MCD,即∠ACE=∠ACM.在△ACE和△ACM中,$\left\{\begin{array}{l} AC=AC,\\ ∠ACE=∠ACM,\\ CE=CM,\end{array}\right. $所以△ACE≌△ACM(SAS),所以AE=AM.因为AM=2AD,所以AE=2AD.
2 [2025 江苏南京质检,较难](1)如图(1),在△ABC 中,AB = 9,AC = 5,求 BC 边上的中线 AD 的取值范围。
(2)如图(2),AD 是△ABC 的中线,AB = AE,AC = AF,∠BAE = ∠FAC = 90°,试探究线段 AD 与 EF 的数量关系和位置关系,并加以证明。
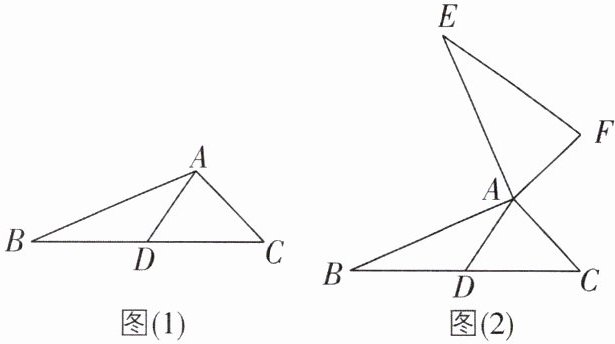
(2)如图(2),AD 是△ABC 的中线,AB = AE,AC = AF,∠BAE = ∠FAC = 90°,试探究线段 AD 与 EF 的数量关系和位置关系,并加以证明。

答案:
(1)如图
(1),延长AD到E,使得DE=AD,连结BE,则AE=2AD.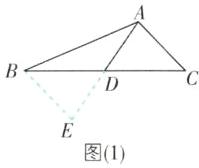
∵D是BC的中点,
∴BD=CD.在△ACD和△EBD中,$\left\{\begin{array}{l} CD=BD,\\ ∠ADC=∠EDB,\\ AD=DE,\end{array}\right. $
∴△ACD≌△EBD(SAS),
∴BE=AC.在△ABE中,由三角形的三边关系可得AB - BE<AE<AB + BE,即AB - BE<2AD<AB + BE.
∵AB=9,AC=BE=5,
∴9 - 5<2AD<9 + 5,
∴2<AD<7,
∴BC边上的中线AD的取值范围为2<AD<7.
(2)EF=2AD且EF⊥AD,证明如下:如图
(2),延长AD到G,使得DG=AD,连结BG,延长DA交EF于点H. 同
同
(1)可证△ACD≌△GBD,
∴AC=BG,∠DAC=∠DGB,
∴∠BAC =∠BAD + ∠DAC=∠BAD + ∠DGB,
∴∠ABG + ∠BAD + ∠DGB=∠ABG + ∠BAC=180°.
∵∠BAE=∠FAC=90°,
∴∠EAF + ∠BAC=180°,
∴∠EAF=∠ABG.
∵AC=AF,AC=BG,
∴BG=AF.在△ABG和△EAF中,$\left\{\begin{array}{l} AB=AE,\\ ∠ABG=∠EAF,\\ BG=AF,\end{array}\right. $
∴△ABG≌△EAF(SAS),
∴EF=AG,∠HEA=∠BAG.
∵AG=2AD,
∴EF=2AD.
∵∠BAE=90°,
∴∠EAH + ∠BAG=90°.
∵∠HEA=∠BAG,
∴∠HEA + ∠EAH=90°,
∴∠AHE=90°,
∴AD⊥EF.综上所述,EF=2AD且EF⊥AD.
(1)如图
(1),延长AD到E,使得DE=AD,连结BE,则AE=2AD.

∵D是BC的中点,
∴BD=CD.在△ACD和△EBD中,$\left\{\begin{array}{l} CD=BD,\\ ∠ADC=∠EDB,\\ AD=DE,\end{array}\right. $
∴△ACD≌△EBD(SAS),
∴BE=AC.在△ABE中,由三角形的三边关系可得AB - BE<AE<AB + BE,即AB - BE<2AD<AB + BE.
∵AB=9,AC=BE=5,
∴9 - 5<2AD<9 + 5,
∴2<AD<7,
∴BC边上的中线AD的取值范围为2<AD<7.
(2)EF=2AD且EF⊥AD,证明如下:如图
(2),延长AD到G,使得DG=AD,连结BG,延长DA交EF于点H.
 同
同(1)可证△ACD≌△GBD,
∴AC=BG,∠DAC=∠DGB,
∴∠BAC =∠BAD + ∠DAC=∠BAD + ∠DGB,
∴∠ABG + ∠BAD + ∠DGB=∠ABG + ∠BAC=180°.
∵∠BAE=∠FAC=90°,
∴∠EAF + ∠BAC=180°,
∴∠EAF=∠ABG.
∵AC=AF,AC=BG,
∴BG=AF.在△ABG和△EAF中,$\left\{\begin{array}{l} AB=AE,\\ ∠ABG=∠EAF,\\ BG=AF,\end{array}\right. $
∴△ABG≌△EAF(SAS),
∴EF=AG,∠HEA=∠BAG.
∵AG=2AD,
∴EF=2AD.
∵∠BAE=90°,
∴∠EAH + ∠BAG=90°.
∵∠HEA=∠BAG,
∴∠HEA + ∠EAH=90°,
∴∠AHE=90°,
∴AD⊥EF.综上所述,EF=2AD且EF⊥AD.
3 [中]如图,已知四边形 ABCD 中,AD//BC,若∠DAB 的平分线 AE 交 CD 于 E,连结 BE,且 BE 恰好平分∠ABC,则 AB 的长与 AD + BC 长度的大小关系是( )

A.AB > AD + BC
B.AB < AD + BC
C.AB = AD + BC
D.无法确定

A.AB > AD + BC
B.AB < AD + BC
C.AB = AD + BC
D.无法确定
答案:
C 【解析】补短法:如图
(1),延长AE交BC延长线于F.因为AD//CB,所以∠CBA + ∠BAD=180°.因为BE平分∠CBA,AE平分∠BAD,所以∠EBA + ∠BAE=90°,所以∠BEA=180° - 90°=90°,所以∠BEF=∠BEA=90°.在△ABE和△FBE中,$\left\{\begin{array}{l} ∠ABE=∠FBE,\\ BE=BE,\\ ∠AEB=∠FEB,\end{array}\right. $所以△ABE≌△FBE(ASA),所以BA=BF,AE=FE.因为AD//CB,所以∠EAD=∠F.在△ADE和△FCE中,$\left\{\begin{array}{l} ∠EAD=∠F,\\ AE=EF,\\ ∠AED=∠FEC,\end{array}\right. $所以△ADE≌△FCE(ASA),所以AD=CF,所以AB=BC + CF=BC + AD.故选C.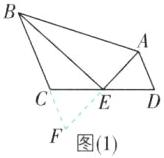
截长法:如图
(2),在AB上截取AF=AD,连结EF.因为AD//BC,所以∠ABC + ∠DAB=180°.又因为BE平分∠ABC,AE平分∠DAB,所以∠ABE + ∠EAB=$\frac{1}{2}$(∠ABC + ∠DAB)=90°,所以∠AEB=90°,即∠2 + ∠4=90°.在△ADE和△AFE中,$\left\{\begin{array}{l} AD=AF,\\ ∠DAE=∠FAE,\\ AE=AE,\end{array}\right. $所以△ADE≌△AFE(SAS),所以∠1=∠2.又因为∠2 + ∠4=90°,∠1 + ∠3=90°,所以∠3=∠4.在△BCE和△BFE中,$\left\{\begin{array}{l} ∠CBE=∠FBE,\\ BE=BE,\\ ∠3=∠4,\end{array}\right. $所以△BCE≌△BFE(ASA),所以BC=BF,所以AB=AF + BF=AD + BC.故选C.
C 【解析】补短法:如图
(1),延长AE交BC延长线于F.因为AD//CB,所以∠CBA + ∠BAD=180°.因为BE平分∠CBA,AE平分∠BAD,所以∠EBA + ∠BAE=90°,所以∠BEA=180° - 90°=90°,所以∠BEF=∠BEA=90°.在△ABE和△FBE中,$\left\{\begin{array}{l} ∠ABE=∠FBE,\\ BE=BE,\\ ∠AEB=∠FEB,\end{array}\right. $所以△ABE≌△FBE(ASA),所以BA=BF,AE=FE.因为AD//CB,所以∠EAD=∠F.在△ADE和△FCE中,$\left\{\begin{array}{l} ∠EAD=∠F,\\ AE=EF,\\ ∠AED=∠FEC,\end{array}\right. $所以△ADE≌△FCE(ASA),所以AD=CF,所以AB=BC + CF=BC + AD.故选C.

截长法:如图
(2),在AB上截取AF=AD,连结EF.因为AD//BC,所以∠ABC + ∠DAB=180°.又因为BE平分∠ABC,AE平分∠DAB,所以∠ABE + ∠EAB=$\frac{1}{2}$(∠ABC + ∠DAB)=90°,所以∠AEB=90°,即∠2 + ∠4=90°.在△ADE和△AFE中,$\left\{\begin{array}{l} AD=AF,\\ ∠DAE=∠FAE,\\ AE=AE,\end{array}\right. $所以△ADE≌△AFE(SAS),所以∠1=∠2.又因为∠2 + ∠4=90°,∠1 + ∠3=90°,所以∠3=∠4.在△BCE和△BFE中,$\left\{\begin{array}{l} ∠CBE=∠FBE,\\ BE=BE,\\ ∠3=∠4,\end{array}\right. $所以△BCE≌△BFE(ASA),所以BC=BF,所以AB=AF + BF=AD + BC.故选C.

4 [2025 吉林长春期末,中]“截长补短法”是作辅助线的常用方法。截长法:在较长的线段上截取一条线段等于较短线段;补短法:延长较短线段使其和较长线段相等。这两种方法统称截长补短法。请用其中一种方法解决下列问题:如图,在△ABC 中,AB > AC,∠1 = ∠2,P 为 AD 上任一点,求证:AB - AC > PB - PC。
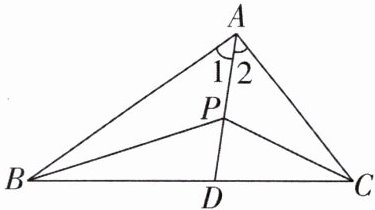

答案:
【证明】证法一:如图
(1),在AB上截取AN,使AN=AC,连结PN.在△ANP和△ACP中,$\left\{\begin{array}{l} AN=AC,\\ ∠1=∠2,\\ AP=AP,\end{array}\right. $
∴△ANP≌△ACP(SAS),
∴PN=PC.在△PBN中,BN>PB - PN,即AB - AC>PB - PC.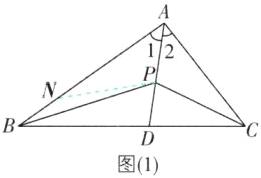
证法二:如图
(2),延长AC到M,使AM=AB,连结PM.在△AMP和△ABP中,$\left\{\begin{array}{l} AM=AB,\\ ∠2=∠1,\\ AP=AP,\end{array}\right. $
∴△AMP≌△ABP(SAS),
∴PM=PB.在△PCM中,CM>PM - PC,即AB - AC>PB - PC.(选择其中一种证法即可)
【证明】证法一:如图
(1),在AB上截取AN,使AN=AC,连结PN.在△ANP和△ACP中,$\left\{\begin{array}{l} AN=AC,\\ ∠1=∠2,\\ AP=AP,\end{array}\right. $
∴△ANP≌△ACP(SAS),
∴PN=PC.在△PBN中,BN>PB - PN,即AB - AC>PB - PC.

证法二:如图
(2),延长AC到M,使AM=AB,连结PM.在△AMP和△ABP中,$\left\{\begin{array}{l} AM=AB,\\ ∠2=∠1,\\ AP=AP,\end{array}\right. $
∴△AMP≌△ABP(SAS),
∴PM=PB.在△PCM中,CM>PM - PC,即AB - AC>PB - PC.(选择其中一种证法即可)

5 [2024 山东菏泽校级质检,中]如图,在 Rt△ABC 中,∠ACB = 90°,∠BAC 的平分线 AD 交 BC 于 D,交∠ABC 的平分线于 E,过点 E 作 EF⊥AE,交 AC 于点 F,试说明:AF + BD = AB。


答案:
延长EF,BC,交于点M,如图. 因为∠ACB=90°,所以∠CAB + ∠CBA=90°.因为AE平分∠BAC,BE平分∠ABC,所以∠EAB + ∠EBA=45°,所以∠AEB=180° - 45°=135°,所以∠DEB=180° - 135°=45°.因为AE⊥EF,所以∠MEB=∠MED + ∠DEB=90° + 45°=135°=∠AEB.在△AEB和△MEB中,$\left\{\begin{array}{l} ∠AEB=∠MEB,\\ EB=EB,\\ ∠ABE=∠MBE,\end{array}\right. $所以△AEB≌△MEB(ASA),所以∠EAB=∠M,AE=ME,AB=MB.因为AE平分∠BAC,所以∠FAE=∠EAB,所以∠FAE=∠M.在△AEF和△MED中,$\left\{\begin{array}{l} ∠FAE=∠M,\\ AE=ME,\\ ∠AEF=∠MED=90°,\\ \end{array}\right. $所以△AEF≌△MED(ASA),所以AF=MD,所以AF + BD=MD + BD=MB=AB.
因为∠ACB=90°,所以∠CAB + ∠CBA=90°.因为AE平分∠BAC,BE平分∠ABC,所以∠EAB + ∠EBA=45°,所以∠AEB=180° - 45°=135°,所以∠DEB=180° - 135°=45°.因为AE⊥EF,所以∠MEB=∠MED + ∠DEB=90° + 45°=135°=∠AEB.在△AEB和△MEB中,$\left\{\begin{array}{l} ∠AEB=∠MEB,\\ EB=EB,\\ ∠ABE=∠MBE,\end{array}\right. $所以△AEB≌△MEB(ASA),所以∠EAB=∠M,AE=ME,AB=MB.因为AE平分∠BAC,所以∠FAE=∠EAB,所以∠FAE=∠M.在△AEF和△MED中,$\left\{\begin{array}{l} ∠FAE=∠M,\\ AE=ME,\\ ∠AEF=∠MED=90°,\\ \end{array}\right. $所以△AEF≌△MED(ASA),所以AF=MD,所以AF + BD=MD + BD=MB=AB.
延长EF,BC,交于点M,如图.
 因为∠ACB=90°,所以∠CAB + ∠CBA=90°.因为AE平分∠BAC,BE平分∠ABC,所以∠EAB + ∠EBA=45°,所以∠AEB=180° - 45°=135°,所以∠DEB=180° - 135°=45°.因为AE⊥EF,所以∠MEB=∠MED + ∠DEB=90° + 45°=135°=∠AEB.在△AEB和△MEB中,$\left\{\begin{array}{l} ∠AEB=∠MEB,\\ EB=EB,\\ ∠ABE=∠MBE,\end{array}\right. $所以△AEB≌△MEB(ASA),所以∠EAB=∠M,AE=ME,AB=MB.因为AE平分∠BAC,所以∠FAE=∠EAB,所以∠FAE=∠M.在△AEF和△MED中,$\left\{\begin{array}{l} ∠FAE=∠M,\\ AE=ME,\\ ∠AEF=∠MED=90°,\\ \end{array}\right. $所以△AEF≌△MED(ASA),所以AF=MD,所以AF + BD=MD + BD=MB=AB.
因为∠ACB=90°,所以∠CAB + ∠CBA=90°.因为AE平分∠BAC,BE平分∠ABC,所以∠EAB + ∠EBA=45°,所以∠AEB=180° - 45°=135°,所以∠DEB=180° - 135°=45°.因为AE⊥EF,所以∠MEB=∠MED + ∠DEB=90° + 45°=135°=∠AEB.在△AEB和△MEB中,$\left\{\begin{array}{l} ∠AEB=∠MEB,\\ EB=EB,\\ ∠ABE=∠MBE,\end{array}\right. $所以△AEB≌△MEB(ASA),所以∠EAB=∠M,AE=ME,AB=MB.因为AE平分∠BAC,所以∠FAE=∠EAB,所以∠FAE=∠M.在△AEF和△MED中,$\left\{\begin{array}{l} ∠FAE=∠M,\\ AE=ME,\\ ∠AEF=∠MED=90°,\\ \end{array}\right. $所以△AEF≌△MED(ASA),所以AF=MD,所以AF + BD=MD + BD=MB=AB. 查看更多完整答案,请扫码查看


