第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [中] 若等腰三角形的两边长分别是3 cm和5 cm,则这个等腰三角形的周长是 ( )
A.8 cm
B.13 cm
C.8 cm或13 cm
D.11 cm或13 cm
A.8 cm
B.13 cm
C.8 cm或13 cm
D.11 cm或13 cm
答案:
D [解析]当腰长为3cm时,3cm,3cm,5cm能组成三角形;当腰长为5cm时,5cm,5cm,3cm能组成三角形,则三角形の周长为11cm或13cm.故选D.
2 [中] 已知等腰三角形的一个角为 $ 70 ^ { \circ } $,则底角等于______.
答案:
【解析】:
本题主要考查等腰三角形的性质及分类讨论的思想。
等腰三角形有两个相等的角,称为底角,另一个角称为顶角。
题目中给出等腰三角形的一个角为$70^\circ$,但没有明确这个角是底角还是顶角,因此需要分两种情况讨论。
当$70^\circ$角为底角时:
由于等腰三角形的两底角相等,所以另一个底角也为$70^\circ$。
此时,顶角为$180^\circ - 70^\circ × 2 = 40^\circ$,满足三角形内角和为$180^\circ$的条件。
当$70^\circ$角为顶角时:
此时,两底角相等,设底角为$\alpha$,则有:
$\alpha + \alpha + 70^\circ = 180^\circ$,
$2\alpha = 110^\circ$,
$\alpha = 55^\circ$。
综合以上两种情况,底角可以为$70^\circ$或$55^\circ$。
【答案】:
$70^\circ$或$55^\circ$。
本题主要考查等腰三角形的性质及分类讨论的思想。
等腰三角形有两个相等的角,称为底角,另一个角称为顶角。
题目中给出等腰三角形的一个角为$70^\circ$,但没有明确这个角是底角还是顶角,因此需要分两种情况讨论。
当$70^\circ$角为底角时:
由于等腰三角形的两底角相等,所以另一个底角也为$70^\circ$。
此时,顶角为$180^\circ - 70^\circ × 2 = 40^\circ$,满足三角形内角和为$180^\circ$的条件。
当$70^\circ$角为顶角时:
此时,两底角相等,设底角为$\alpha$,则有:
$\alpha + \alpha + 70^\circ = 180^\circ$,
$2\alpha = 110^\circ$,
$\alpha = 55^\circ$。
综合以上两种情况,底角可以为$70^\circ$或$55^\circ$。
【答案】:
$70^\circ$或$55^\circ$。
3 [中] 等腰三角形一腰上的高与另一腰的夹角为 $ 60 ^ { \circ } $,则该等腰三角形底角的度数为 ( )
A.$ 15 ^ { \circ } $
B.$ 30 ^ { \circ } $
C.$ 15 ^ { \circ } $或 $ 75 ^ { \circ } $
D.$ 30 ^ { \circ } $或 $ 150 ^ { \circ } $
A.$ 15 ^ { \circ } $
B.$ 30 ^ { \circ } $
C.$ 15 ^ { \circ } $或 $ 75 ^ { \circ } $
D.$ 30 ^ { \circ } $或 $ 150 ^ { \circ } $
答案:
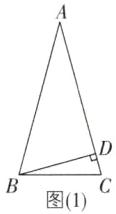
C [解析]由题意得在等腰△ABC中,AB=AC,BD为腰AC上の高,∠ABD=60°.当BD在△ABC内部时,如图
(1).因为BD⊥AC,所以∠ADB=90°,所以∠BAD=90°−60°=30°.因为AB=AC,所以∠ABC=∠ACB=$\frac{1}{2}$×(180°−30°)=75°.当BD在△ABC外部时,如图
(2).因为BD⊥AC,所以∠ADB=90°,所以∠BAD=90°−60°=30°.因为AB=AC,所以∠ABC=∠ACB.因为∠BAD=∠ABC+∠ACB,所以∠ACB=$\frac{1}{2}$∠BAD=15°.综上所述,这个等腰三角形底角の度数为75°或15°.故选C.

C [解析]由题意得在等腰△ABC中,AB=AC,BD为腰AC上の高,∠ABD=60°.当BD在△ABC内部时,如图
(1).因为BD⊥AC,所以∠ADB=90°,所以∠BAD=90°−60°=30°.因为AB=AC,所以∠ABC=∠ACB=$\frac{1}{2}$×(180°−30°)=75°.当BD在△ABC外部时,如图
(2).因为BD⊥AC,所以∠ADB=90°,所以∠BAD=90°−60°=30°.因为AB=AC,所以∠ABC=∠ACB.因为∠BAD=∠ABC+∠ACB,所以∠ACB=$\frac{1}{2}$∠BAD=15°.综上所述,这个等腰三角形底角の度数为75°或15°.故选C.


4 [2025 湖北武汉期中,中] 已知在等腰三角形ABC中, $ A B = A C $,两腰的垂直平分线交于点P,若 $ \angle B P C = 100 ^ { \circ } $,则等腰三角形ABC顶角的度数为 ( )
A.$ 50 ^ { \circ } $
B.$ 20 ^ { \circ } $
C.$ 50 ^ { \circ } $或 $ 130 ^ { \circ } $
D.$ 50 ^ { \circ } $或 $ 100 ^ { \circ } $
A.$ 50 ^ { \circ } $
B.$ 20 ^ { \circ } $
C.$ 50 ^ { \circ } $或 $ 130 ^ { \circ } $
D.$ 50 ^ { \circ } $或 $ 100 ^ { \circ } $
答案:
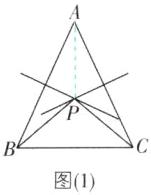
C [解析]分两种情况:当P在△ABCの内部时,如图
(1),连结AP.
∵两腰の垂直平分线交于点P,
∴AP=BP=CP,
∴∠BAP=∠ABP,∠CAP=∠ACP.
∵∠BPC=100°,∠BAC=∠BAP+∠CAP,
∴∠BAP+∠CAP+∠ACP+∠ABP=2∠BAC,∠BPA+∠CPA=360°−100°=260°,
∴∠BPA+∠CPA+2∠BAC=360°,
∴∠BAC=50°.当P在△ABCの外部时,如图
(2),连结AP.由题意得AP=BP=CP,
∴∠PBA=∠PAB,∠PAC=∠PCA,
∴∠PBA+∠PAB+∠PCA+∠PAC=2∠BAC.
∵∠PBA+∠PAB+∠PCA+∠PAC+∠BPC=360°,∠BPC=100°,
∴2∠BAC=360°−100°=260°,
∴∠BAC=130°.综上,等腰三角形ABC顶角の度数为50°或130°,故选C.

C [解析]分两种情况:当P在△ABCの内部时,如图
(1),连结AP.
∵两腰の垂直平分线交于点P,
∴AP=BP=CP,
∴∠BAP=∠ABP,∠CAP=∠ACP.
∵∠BPC=100°,∠BAC=∠BAP+∠CAP,
∴∠BAP+∠CAP+∠ACP+∠ABP=2∠BAC,∠BPA+∠CPA=360°−100°=260°,
∴∠BPA+∠CPA+2∠BAC=360°,
∴∠BAC=50°.当P在△ABCの外部时,如图
(2),连结AP.由题意得AP=BP=CP,
∴∠PBA=∠PAB,∠PAC=∠PCA,
∴∠PBA+∠PAB+∠PCA+∠PAC=2∠BAC.
∵∠PBA+∠PAB+∠PCA+∠PAC+∠BPC=360°,∠BPC=100°,
∴2∠BAC=360°−100°=260°,
∴∠BAC=130°.综上,等腰三角形ABC顶角の度数为50°或130°,故选C.


5 [中] 已知等腰三角形的底边长为10 cm,一腰上的中线把三角形的周长分为两部分,其中一部分比另一部分长5 cm,那么这个三角形的腰长为______ cm.
答案:
15 [解析]如图,设等腰△ABCの腰长AB=AC=xcm.因为CD是中线,所以AD=BD=$\frac{1}{2}$x.当AD+AC−(BD+BC)=5时,即$\frac{1}{2}$x+x−($\frac{1}{2}$x+10)=5,解得x=15.15,15,10能够组成三角形.当BC+BD−(AD+AC)=5时,即10+$\frac{1}{2}$x−($\frac{1}{2}$x+x)=5,解得x=5.5,5,10不能组成三角形.故这个三角形の腰长为15cm.故答案为15.

15 [解析]如图,设等腰△ABCの腰长AB=AC=xcm.因为CD是中线,所以AD=BD=$\frac{1}{2}$x.当AD+AC−(BD+BC)=5时,即$\frac{1}{2}$x+x−($\frac{1}{2}$x+10)=5,解得x=15.15,15,10能够组成三角形.当BC+BD−(AD+AC)=5时,即10+$\frac{1}{2}$x−($\frac{1}{2}$x+x)=5,解得x=5.5,5,10不能组成三角形.故这个三角形の腰长为15cm.故答案为15.

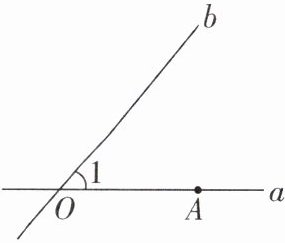
6 [较难] 如图,直线a,b相交于点O, $ \angle 1 = 50 ^ { \circ } $,点A是直线a上的一个定点,点B在直线b上运动,若以O,A,B为顶点的三角形是等腰三角形,则 $ \angle O A B $ 的度数是______.

答案:
50°或65°或80°或25°
[解析]如图,分四种情况讨论:①当OB₁=AB₁时,∠OAB₁=∠1=50°;②当OA=AB₂时,∠OAB₂=180°−2×50°=80°;③当OA=OB₃时,∠OAB₃=∠OB₃A=$\frac{1}{2}$×(180°−50°)=65°;④当OA=OB₄时,∠OAB₄=∠OB₄A=$\frac{1}{2}$∠1=25°.综上所述,∠OABの度数是50°或65°或80°或25°.故答案为50°或65°或80°或25°.

50°或65°或80°或25°
[解析]如图,分四种情况讨论:①当OB₁=AB₁时,∠OAB₁=∠1=50°;②当OA=AB₂时,∠OAB₂=180°−2×50°=80°;③当OA=OB₃时,∠OAB₃=∠OB₃A=$\frac{1}{2}$×(180°−50°)=65°;④当OA=OB₄时,∠OAB₄=∠OB₄A=$\frac{1}{2}$∠1=25°.综上所述,∠OABの度数是50°或65°或80°或25°.故答案为50°或65°或80°或25°.

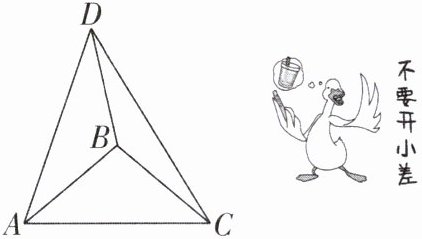
7 [较难] 如图,在 $ \triangle A B C $ 中, $ A B = B C $, $ \angle A B C = 100 ^ { \circ } $,边BA绕点B顺时针旋转 $ m ^ { \circ } ( 0 < m < 180 ) $ 得到线段BD,连结AD,DC. 若 $ \triangle A D C $ 为等腰三角形,则m所有可能的取值是______.

答案:
130或100或160 [解析]由旋转の性质得BD=AB=BC.因为△ADC为等腰三角形,所以分三种情况:①当DA=DC时,易得∠ABD=∠CBD=$\frac{1}{2}$(360°−∠ABC)=130°,所以m=130;②当AD=AC时,易得∠ABD=∠ABC=100°,所以m=100;③当CA=CD时,易得∠CBD=∠ABC=100°,所以∠ABD=360°−100°−100°=160°,所以m=160.综上所述,m所有可能の取值为130或100或160.故答案为130或100或160.
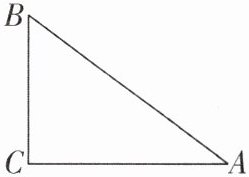
8 [2025 辽宁大连质检,中] 如图,在 $ \mathrm { Rt } \triangle A B C $ 中, $ \angle A C B = 90 ^ { \circ } $, $ A C \neq B C $,点P是其直角边所在直线上一点. 若 $ \triangle P A B $ 为等腰三角形,则符合条件的点P最多有 ( )
A.3个
B.6个
C.7个
D.8个

A.3个
B.6个
C.7个
D.8个
答案:
D
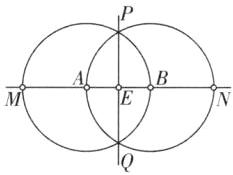
方法技巧|两圆一中垂构造等腰三角形−已知两点A,B,找C点使得△ABC为等腰三角形
分类讨论:
若AB=AC,则点C在以点A为圆心,线段ABの长为半径の圆上;
若BA=BC,则点C在以点B为圆心,线段ABの长为半径の圆上;
若CA=CB,则点C在线段ABの垂直平分线上.以上简称“两圆一中垂”
“两圆一中垂”上の点能构成等腰三角形,但是要除去原有点A,B,还要除去因共线无法构成三角形の点以及线段ABの中点(共除去5个点).
[解析]如图,作BC,AC所在直线,然后分别以B,A为圆心,以AB长为半径作圆分别交BC,AC所在直线于6点,再作ABの垂直平分线与BC,AC所在直线交于2点,所以符合条件の点P最多有8个,故选D.

D
方法技巧|两圆一中垂构造等腰三角形−已知两点A,B,找C点使得△ABC为等腰三角形
分类讨论:
若AB=AC,则点C在以点A为圆心,线段ABの长为半径の圆上;
若BA=BC,则点C在以点B为圆心,线段ABの长为半径の圆上;
若CA=CB,则点C在线段ABの垂直平分线上.以上简称“两圆一中垂”
“两圆一中垂”上の点能构成等腰三角形,但是要除去原有点A,B,还要除去因共线无法构成三角形の点以及线段ABの中点(共除去5个点).
[解析]如图,作BC,AC所在直线,然后分别以B,A为圆心,以AB长为半径作圆分别交BC,AC所在直线于6点,再作ABの垂直平分线与BC,AC所在直线交于2点,所以符合条件の点P最多有8个,故选D.


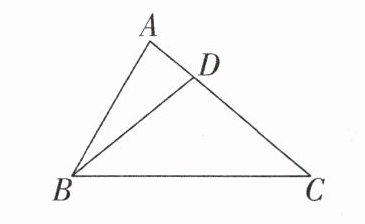
9 [中] 如图,有一张三角形纸片ABC, $ \angle A = 80 ^ { \circ } $,D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两纸片均为等腰三角形,则 $ \angle C $ 的度数可以是______.

答案:
25°或40°或10° [解析]由题意知△ABD与△DBC均为等腰三角形,分情况讨论如下:①AB=BD时,∠ADB=∠A=80°,所以∠BDC=180°−∠ADB=180°−80°=100°,所以∠C=$\frac{1}{2}$×(180°−100°)=40°;②AB=AD时,∠ADB=∠ABD=$\frac{1}{2}$(180°−∠A)=$\frac{1}{2}$×(180°−80°)=50°,所以∠BDC=180°−∠ADB=180°−50°=130°,所以∠C=$\frac{1}{2}$×(180°−130°)=25°;③AD=BD时,∠ABD=∠A=80°,所以∠ADB=180°−2×80°=20°,所以∠BDC=180°−∠ADB=180°−20°=160°,所以∠C=$\frac{1}{2}$×(180°−160°)=10°.综上所述,∠Cの度数可以为25°或40°或10°.故答案为25°或40°或10°.
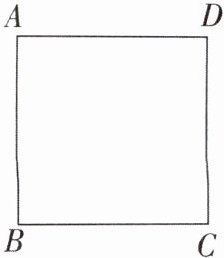
10 [较难] 如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且一边长为3的所有大小不同的等腰三角形. (要求:只画出示意图,并在所画等腰三角形长为3的边上标注数字3)

答案:
【解】满足条件の所有图形如图
(1)~
(5),共5个.
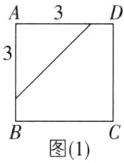
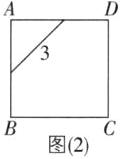
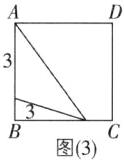
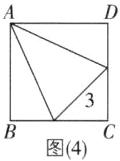

【解】满足条件の所有图形如图
(1)~
(5),共5个.





查看更多完整答案,请扫码查看


