《2025年初中必刷题八年级数学上册华师大版》

1 [2025 黑龙江绥化期末]$\sqrt [3]{64}$的平方根是( )

A.±8
B.±4
C.±2
D.±√2

答案： C　[解析]
∵ $\sqrt [3]{64}=4$，且$(\pm 2)^{2}=4$，
∴ $\sqrt [3]{64}$的平方根是$\pm 2$. 故选C.

2 [2025 四川达州质检]下列等式不成立的是( )

A.$\sqrt [3]{(-2)^{3}}= -2$
B.$\sqrt [3]{-8}= -\sqrt [3]{8}$
C.$\sqrt [3]{0.0729}= 0.9$
D.$(\sqrt [3]{-13})^{3}= -13$

答案： C　[解析]A选项，$\sqrt [3]{(-2)^{3}}=-2$，故此选项正确；B选项，$\sqrt [3]{-8}=-\sqrt [3]{8}$，故此选项正确；C选项，$0.9^{3}=0.729$，所以$\sqrt [3]{0.0729}≠0.9$，故此选项错误；D选项，$(\sqrt [3]{-13})^{3}=-13$，故此选项正确. 故选C.

3 [2025 山西晋城期中]下列说法正确的是( )

A.如果一个数的立方根是这个数本身,那么这个数一定是 0
B.一个数的立方根不是正数就是负数
C.负数没有立方根
D.一个不为 0 的数的立方根和这个数同号

答案： D　[解析]A选项，如果一个数的立方根是这个数本身，那么这个数一定是0或1或−1，故此选项说法错误；B选项，一个数的立方根可能是正数、负数或0，故此选项说法错误；C选项，负数有立方根，故此选项说法错误；D选项，一个不为0的数的立方根和这个数同号，故此选项说法正确. 故选D.

4 若$a^{2}= 16,\sqrt [3]{b}= 2$,则$a+b$的值为( )

A.12
B.4
C.12 或-4
D.12 或 4

答案： D　[解析]
∵$a^{2}=16$，
∴$a=\pm 4$.
∵$\sqrt [3]{b}=2$，
∴$b=8$，
∴$a+b=4+8=12$或$−4+8=4$. 故选D.

5 [2025 河南洛阳质检]若$\sqrt {x}= 2,y^{3}= -27$,则$x+y= $____.

答案： 1　[解析]
∵$\sqrt{x}=2$，$y^{3}=−27$，
∴$x=4$，$y=−3$，
∴$x+y=4−3=1$. 故答案为1.

6 [2025 山西临汾期末]若$\sqrt [3]{2-a}= -\sqrt [3]{b-3}$,则$b-a+3$的平方根为____.

答案： ±2　[解析]
∵$\sqrt [3]{2-a}=-\sqrt [3]{b-3}$，
∴$\sqrt [3]{2-a}=\sqrt [3]{3-b}$，
∴$2-a=3-b$，
∴$b-a=3-2=1$，
∴$b-a+3=1+3=4$，
∴$b-a+3$的平方根是$\pm 2$.

7 [2025 四川宜宾期中]求下列各数的立方根.
(1)$3\frac {3}{8}$;
(2)-729;
(3)0.343;
(4)$\frac {512}{1331}$.

答案： [解]
(1)
∵$3\frac{3}{8}=\frac{27}{8}$，$(\frac{3}{2})^{3}=\frac{27}{8}$，
∴$3\frac{3}{8}$的立方根是$\frac{3}{2}$.
(2)
∵$(-9)^{3}=−729$，
∴$−729$的立方根是$−9$.
(3)
∵$(0.7)^{3}=0.343$，
∴$0.343$的立方根是$0.7$.
(4)
∵$(\frac{8}{11})^{3}=\frac{512}{1331}$，
∴$\frac{512}{1331}$的立方根是$\frac{8}{11}$.

8 用计算器计算:
(1)$\sqrt [3]{0.9578}\approx $____.(精确到 0.01)
(2)$\sqrt [3]{-15786}\approx $____.(精确到 0.001)

答案：
(1)0.99
(2)−25.086
[解析]
(1)$\sqrt [3]{0.9578}\approx 0.99$.
(2)$\sqrt [3]{-15786}\approx -25.086$.

9 [2025 四川内江期末]如图所示的零件是由两个正方体焊接而成,已知大正方体和小正方体的体积分别为$125cm^{3}和27cm^{3}$,现要给这个零件的表面(包括底面)刷上油漆,那么所刷油漆的面积是( )


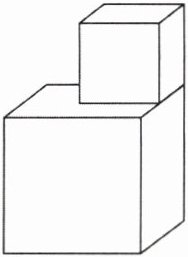
A.$161cm^{2}$
B.$186cm^{2}$
C.$195cm^{2}$
D.$204cm^{2}$

答案： B　[解析]
∵大正方体的体积为$125cm^{3}$，小正方体的体积为$27cm^{3}$，
∴大正方体的棱长为$\sqrt [3]{125}=5(cm)$，小正方体的棱长为$\sqrt [3]{27}=3(cm)$，
∴这个零件的表面积为$5×5×6+3×3×4=186(cm^{2})$，则所刷油漆的面积为$186cm^{2}$. 故选B.

10 [2025 浙江金华期中]如图(示意图),一个底面半径为 3 cm 的瓶子(下半部分是圆柱)内装着一些溶液.当瓶子正放时,瓶内溶液的高度为 16 cm;当瓶子倒放时,空余部分的高度为 4 cm.瓶内的溶液正好倒满 2 个一样大的正方体容器(π取 3,容器的厚度忽略不计).
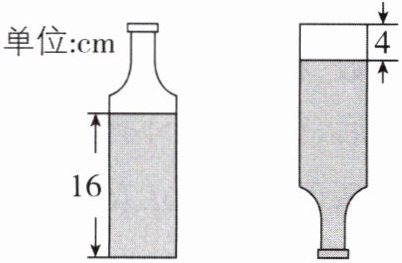
(1)该瓶子的容积(装满时溶液的体积)是多少立方厘米?
(2)正方体容器的棱长是多少厘米?

答案： [解]
(1)该瓶子的容积$V=πr^{2}h=3×9×(16+4)=27×20=540(cm^{3})$.
(2)因为瓶内溶液的体积为$3×3^{2}×16=432(cm^{3})$，所以正方体容器的棱长为$\sqrt [3]{432÷2}=6(cm)$.