《2025年初中必刷题八年级数学上册华师大版》

1 [2025 浙江杭州拱墅区质检，中]如图，$AB = AC$，$AD = AE$，$∠BAC = ∠DAE$，$∠1 = 26^{\circ}$，$∠2 = 33^{\circ}$，连结$BE$，点$D$恰好在$BE$上，则$∠3 =$（ ）

A.$60^{\circ}$
B.$59^{\circ}$
C.$61^{\circ}$
D.无法计算

答案： 1. B 【解析】
∵∠BAC=∠DAE，即∠1+∠DAC=∠DAC+∠CAE，
∴∠1=∠CAE.在△ABD和△ACE中，$\left\{\begin{array}{l} AB=AC,\\ ∠1=∠CAE,\\ AD=AE,\end{array}\right. $
∴△ABD≌△ACE(SAS)，
∴∠ABD=∠2=33°，
∴∠3=∠1+∠ABD=26°+33°=59°.故选B.

2 新考法[2025 四川成都期中，中]如图，由$3×3$个完全相同的小正方形组成的网格中，$A$，$B$，$C$，$D$均为格点，设$∠ABC = \alpha$，$∠BCD = \beta$，$∠BAD = \gamma$，则$\alpha - \beta - \gamma$的值为（ ）

A.$45^{\circ}$
B.$60^{\circ}$
C.$75^{\circ}$
D.$135^{\circ}$

答案：
2. A 【解析】如图，取格点E，F，G.
∵BE=AG，∠BEC=∠AGB=90°，EC=GB，
∴△BEC≌△AGB(SAS)，
∴∠ECB=∠GBA.
∵∠ECB+∠EBC=90°，
∴∠GBA+∠EBC=90°，
∴∠ABC=90°=α.
∵β+∠CBD=90°，∠CBD+∠ABD=90°，
∴∠ABD=β.
∵∠ADF=∠ABD+∠BAD=45°，
∴β+γ=45°，
∴α - β - γ=90° - 45°=45°.故选A.

3 [较难]如图，在$\triangle ABC$和$\triangle BCD$中，$BD$，$CA$分别平分$∠ABC$和$∠BCD$，$BD$与$AC$相交于点$E$，若$∠D = 89^{\circ}$，$BC = AB + CD$，则$∠ABC$等于（ ）

A.$60^{\circ}$
B.$62^{\circ}$
C.$58^{\circ}$
D.$59^{\circ}$

答案：
3. C 【解析】如图，在BC上截取BF=AB，连结EF.因为BC=AB+CD，所以BC=BF+CD.又因为BC=BF+CF，所以CD=CF.因为BD，CA分别平分∠ABC和∠BCD，所以∠ABE=∠EBC，∠DCE=∠ECB.因为AB=BF，∠ABE=∠EBC，BE=BE，所以△ABE≌△FBE(SAS)，所以∠A=∠BFE.因为CD=CF，∠DCE=∠ECF，EC=EC，所以△DCE≌△FCE(SAS)，所以∠D=∠EFC=89°.因为∠BFE+∠EFC=180°，所以∠BFE=91°=∠A.因为∠A+∠ABC+∠ACB=180°，所以∠ABC+$\frac{1}{2}$∠DCB=89°.① 因为∠D+∠DCB+∠DBC=180°，所以∠DCB+$\frac{1}{2}$∠ABC=91°.② 由①②组成方程组可得∠ABC=58°.故选C.

4 [中]如图，已知$AB = AD$，$BC = DE$，且$∠CAD = 20^{\circ}$，$∠B = ∠D = 25^{\circ}$，$∠EAB = 120^{\circ}$，则$∠EGB$的度数为______.

答案： 4. 110° 【解析】在△ABC和△ADE中，$\left\{\begin{array}{l} AB=AD,\\ ∠B=∠D,\\ BC=DE,\end{array}\right. $
∴△ABC≌△ADE(SAS)，
∴∠DAE=∠CAB.
∵∠EAB=120°，∠CAD=20°，
∴∠EAD=∠CAB=50°，
∴∠DAB=70°.
∵∠DGB+∠D=∠DAB+∠B，∠B=∠D=25°，
∴∠DGB=∠DAB=70°，
∴∠EGB=110°.故答案为110°.

5 [中]如图，四边形$ABCD$中，$AB = BC = 2CD$，$AB// CD$，$∠C = 90^{\circ}$，$E$是$BC$的中点，$AE$与$BD$相交于点$F$，连结$DE$.
（1）求证：$\triangle ABE\cong\triangle BCD$.
（2）判断线段$AE$与$BD$的数量关系及位置关系，并说明理由.

答案： 5.
(1)【证明】
∵AB//CD，
∴∠ABE+∠C=180°.
∵∠C=90°，
∴∠ABE=90°=∠C.
∵E是BC的中点，
∴BC=2BE.
∵BC=2CD，
∴BE=CD.在△ABE和△BCD中，$\left\{\begin{array}{l} AB=BC,\\ ∠ABE=∠C,\\ BE=CD,\end{array}\right. $
∴△ABE≌△BCD(SAS).
(2)【解】AE=BD且AE⊥BD.理由如下：由
(1)得△ABE≌△BCD，
∴AE=BD，∠BAE=∠CBD.
∵∠ABF+∠CBD=90°，
∴∠ABF+∠BAE=90°，
∴∠AFB=90°，
∴AE⊥BD.

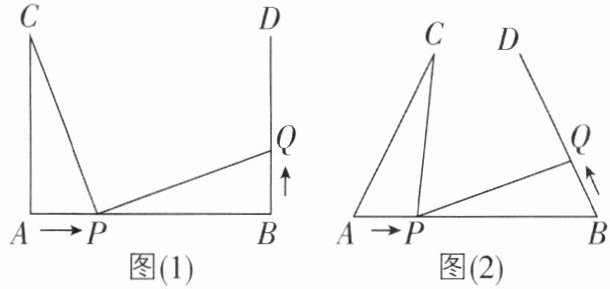
6 核心素养推理能力[较难]如图（1），$AB = 7\ cm$，$AC\perp AB$，$BD\perp AB$，垂足分别为$A$，$B$，$AC = 5\ cm$. 点$P$在线段$AB$上以$2\ cm/s$的速度由点$A$向点$B$运动，同时点$Q$在射线$BD$上运动. 它们运动的时间为$t\ s$，当点$P$运动结束时，点$Q$运动随之结束.
（1）若点$Q$的运动速度与点$P$的运动速度相等，当$t = 1$时，$\triangle ACP$与$\triangle BPQ$是否全等，并判断此时线段$PC$和线段$PQ$的位置关系，请分别说明理由；
（2）如图（2），若“$AC\perp AB$，$BD\perp AB$”改为“$∠CAB = ∠DBA$”，点$Q$的运动速度为$x\ cm/s$，其他条件不变，当点$P$，$Q$运动到某处时，有$\triangle ACP$与$\triangle BPQ$全等，求出相应的$x$，$t$的值.

答案： 6.【解】
(1)△ACP≌△BPQ，PC⊥PQ.理由如下：
∵AC⊥AB，BD⊥AB，
∴∠A=∠B=90°.
∵点Q与点P的运动速度相等，
∴当t=1时，AP=BQ=2cm.
∵AB=7cm，
∴BP=5cm，
∴BP=AC.在△ACP和△BPQ中，$\left\{\begin{array}{l} AP=BQ,\\ ∠A=∠B,\\ AC=BP,\end{array}\right. $
∴△ACP≌△BPQ(SAS)，
∴∠C=∠BPQ.
∵∠C+∠APC=90°，
∴∠APC+∠BPQ=90°，
∴∠CPQ=90°，
∴PC⊥PQ.
(2)分两种情况讨论:①若△ACP≌△BPQ，则AC=BP，AP=BQ，可得5=7 - 2t，2t=xt，解得t=1，x=2；②若△ACP≌△BQP，则AC=BQ，AP=BP，可得5=xt，2t=7 - 2t，解得t=$\frac{7}{4}$，x=$\frac{20}{7}$.综上所述，当t=1，x=2或t=$\frac{7}{4}$，x=$\frac{20}{7}$时，△ACP与△BPQ全等.