《2025年初中必刷题八年级数学上册华师大版》

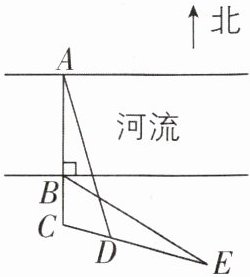
10 [2025山西长治期中,中]某中学几名同学想利用所学知识测量某段河流的宽度(宽度一定),测量方案:他们位于河的南岸,寻找对岸河边一棵树的位置记作点A,在南岸河边寻找点B,使AB垂直于河岸,在南岸平地上取点C,D,使A,B,C三点在同一直线上,且$CB = CD,∠BCD = 105^{\circ }$,测得$∠ADC = 55^{\circ }$,在CD的延长线上取一点E,使$∠BEC = 20^{\circ }$,示意图如图所示,这时测得DE的长就是该段河流的宽度. 你认为这几名同学的测量方案可行吗?请说明理由.

答案： 【解】可行.理由:
∵∠BCD=105°,∠BEC=20°,
∴∠EBC=180° - ∠BCD - ∠BEC=55°.
∵∠ADC=55°,
∴∠ADC=∠EBC.在△ACD和△ECB中,
∵∠ADC=∠EBC,CD=CB,∠ACD=∠ECB,
∴△ACD≌△ECB(ASA),
∴AC=EC.
∵AB=AC - CB,DE=EC - CD,
∴DE=AB,
∴测得DE的长就是该段河流的宽度,
∴这几名同学的测量方案可行.

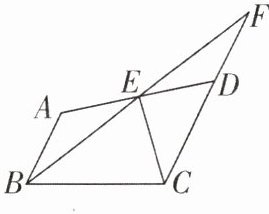
11 [中]如图,在四边形ABCD中,已知$AB// CD$,E是AD边的中点,连结BE并延长,与CD的延长线交于点F.
(1)若$2CD = 3AB$,请判断CD与CF之间的数量关系,并说明理由;
(2)连结CE,若$CE⊥BF$,求证:$AB + CD = BC.$

答案：
(1)【解】CF=$\frac{5}{3}$CD.理由如下:
∵AB//CD,E是AD边的中点,
∴∠ABE=∠DFE,AE=DE.在△ABE和△DFE中,{∠ABE=∠DFE,∠AEB=∠DEF,AE=DE,
∴△ABE≌△DFE(AAS),
∴AB=DF,
∵2CD=3AB=3DF,即DF=$\frac{2}{3}$CD.
∵CF=CD+DF=CD+$\frac{2}{3}$CD=$\frac{5}{3}$CD,
∴CF=$\frac{5}{3}$CD.
(2)【证明】由
(1)可知△ABE≌△DFE,
∴AB=DF,BE=FE.
∵CE⊥BF,
∴∠CEB=∠CEF=90°.在△BEC和△FEC中,{BE=FE,∠CEB=∠CEF,CE=CE,
∴△BEC≌△FEC(SAS),
∴BC=FC,
∴AB+CD=DF+CD=FC=BC.

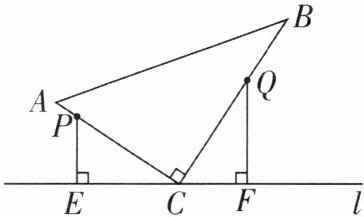
12 [2025吉林长春榆树期中,中]如图,在$△ABC$中,$∠ACB = 90^{\circ },AC = 6,BC = 8$,点C在直线l上. 点P从点A出发,沿折线AC - CB以每秒1个单位长度的速度向终点B运动,点Q从点B出发沿折线BC - CA以每秒3个单位长度的速度向终点A运动,P,Q两点同时出发,分别过P,Q两点作$PE⊥l$于E,$QF⊥l$于F. 设点P的运动时间为t秒.
(1)当P,Q两点相遇时,求t的值;
(2)在整个运动过程中,求CP的长(用含t的代数式表示);
(3)当$△PEC$与$△QFC$全等时,求出所有满足条件的CQ的长.

答案： 【解】
(1)由题意得t+3t=6+8,解得t=$\frac{7}{2}$,故当P,Q两点相遇时,t的值为$\frac{7}{2}$.
(2)由题意可知点P所走过的路程为t,则CP的长为{6 - t(0≤t≤6),t - 6(6 ＜ t≤14).
(3)当P在AC上,Q在BC上时,
∵∠ACB=90°,
∴∠PCE+∠QCF=90°.
∵PE⊥l于E,QF⊥l于F,
∴∠PEC=∠CFQ=90°,
∴∠EPC+∠PCE=90°,
∴∠EPC=∠QCF,
∴当PC=CQ时,△PCE≌△CQF,
∴6 - t=8 - 3t,解得t=1,
∴CQ=8 - 3t=5.当P在AC上,Q在AC上时,易知当P,Q重合时,△PCE≌△QCF,则CQ=PC,由题意得6 - t=3t - 8,解得t=3.5,
∴CQ=3t - 8=2.5.当P在BC上,Q在AC上时,易知A,Q重合,则当CQ=AC=6时,△QFC≌△CEP.综上,当△PEC与△QFC全等时,满足条件的CQ的长为5或2.5或6.

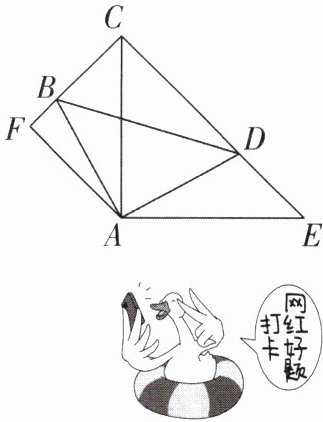
13 [2025湖南常德期末,中]如图,$∠BAD = ∠CAE = 90^{\circ },AB = AD,AE = AC$,D在CE上,$AF⊥CB$交CB延长线于F.
(1)求证:$△ABC\cong △ADE;$
(2)求$∠FAE$的度数;
(3)求证:$CD = 2BF + DE.$

答案：

(1)【证明】
∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,
∴∠BAC=∠DAE.在△BAC和△DAE中,{AB=AD,∠BAC=∠DAE,AC=AE,
∴△BAC≌△DAE(SAS).
(2)【解】
∵∠CAE=90°,AC=AE,
∴∠E=∠ACE=45°.由
(1)知△BAC≌△DAE,
∴∠BCA=∠E=45°.
∵AF⊥BC交CB延长线于F,
∴∠CFA=90°,
∴∠CAF=45°,
∴∠FAE=∠FAC+∠CAE=45°+90°=135°.
(3)【证明】如图,延长BF到G,使得FG=FB,连结AG.

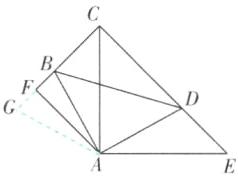
∵AF⊥BG,
∴∠AFG=∠AFB=90°.在△AFB和△AFG中,{BF=GF,∠AFB=∠AFG,AF=AF,
∴△AFB≌△AFG(SAS),
∴AB=AG,∠ABF=∠G,
∴AG=AD.
∵△BAC≌△DAE,
∴∠CBA=∠EDA,CB=ED,
∴∠ABF=∠CDA,
∴∠G=∠CDA.在△CGA和△CDA中,{∠GCA=∠DCA=45°,∠CGA=∠CDA,AG=AD,
∴△CGA≌△CDA(AAS),
∴CG=CD.
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE.