《2025年初中必刷题八年级数学上册华师大版》

1[2025浙江温州鹿城区期中,中]小黄同学计算一道整式乘法:$(x+a)(x+2)$,由于他抄错了a前面的符号,把“+”写成“-”,得到的结果为$x^{2}+bx-4$,则$a+b$的值为( )

A.0
B.2
C.4
D.6

答案： B [解析]由题意得，(x−a)(x+2)=x²+bx−4,
∴x²+(2−a)x−2a=x²+bx−4,
∴2−a=b，−2a=−4,
∴a=2,b=0,
∴a+b=2,故选B.

2[2025广东江门期中,中]如图,通过计算图(1)、图(2)中阴影部分的面积,可以验证的等式是( )


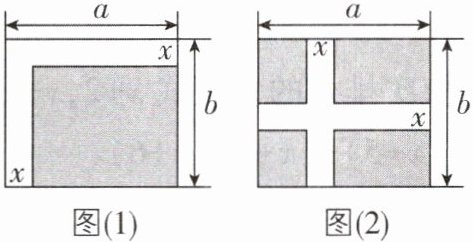
A.$a(b-x)= ab-ax$
B.$(a-x)(b-x)= ab-ax-bx+x^{2}$
C.$(a-x)(b-x)= ab-ax-bx$
D.$b(a-x)= ab-bx$

答案： B [解析]由题意知,题图
(1)和题图
(2)中阴影部分的面积相等.题图
(1)中，阴影部分面积为(a−x)(b−x)，题图
(2)中，阴影部分面积为ab−ax−bx+x²,
∴(a−x)(b−x)=ab−ax−bx+x²,故选B.

3新考向开放性试题[2025上海黄浦区期中,中]已知A是关于x的一次二项式,且$A\cdot (x^{2}-2x)$的积是二项式,请写出一个满足条件的A是____.(只需要写一个即可)

答案： x+2(答案不唯一) [解析]设A=ax+b(a≠0,b≠0),则A·(x²−2x)=(ax+b)·(x²−2x)=ax³−2ax²+bx²−2bx=ax³−(2a−b)x²−2bx.
∵积为二项式,a≠0,b≠0,
∴2a−b=0,
∴a可以为1，b可以为2,
∴A可以是x+2.故答案为x+2(答案不唯一).

4[2025吉林长春期中,中]代数式$1+2x+3x^{2}+4x^{3}与4+3x+2x^{2}+x^{3}的乘积是一个六次多项式ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g$,则$a-b+c-d+e-f+g= $____.

答案： -4 [解析]令x=−1，代入ax⁶+bx⁵+cx⁴+dx³+ex²+fx+g,得a(−1)⁶+b(−1)⁵+c(−1)⁴+d(−1)³+e(−1)²+f(−1)+g=a−b+c−d+e−f+g,将x=−1代入(1+2x+3x²+4x³)(4+3x+2x²+x³),得[1+2×(−1)+3×(−1)²+4×(−1)³]×[4+3×(−1)+2×(−1)²+(−1)³]=(1−2+3−4)×(4−3+2−1)=−2×2=−4,故答案为−4.

5[2025湖南衡阳质检,中]阅读下列材料并解答问题:通过学习,我们知道可以用图(1)中图形的面积来解释代数恒等式$(a+b)^{2}= a^{2}+2ab+b^{2}$,实际上还有一些代数恒等式也可以用这种方式来解释.如图(2),图形的面积可解释恒等式$(2a+b)\cdot (a+2b)= 2a^{2}+5ab+2b^{2}.$



(1)请写出图(3)中图形的面积可以解释的代数恒等式为____;
(2)试画出一个几何图形,可以用该图形的面积解释恒等式:$2a(a+3b)= 2a^{2}+6ab;$
(3)请仿照上述方法另写一个含a,b的代数恒等式,并画出面积可以解释该恒等式的几何图形.

答案：
[解]
(1)题图
(3)中面积的表示为方法一:(a+b)(2a+b),方法二:2a²+3ab+b²,
∴(a+b)(2a+b)=2a²+3ab+b²,故答案为(a+b)(2a+b)=2a²+3ab+b².
(2)如图
(1)所示.

面积表示为方法一:2a(a+3b),方法二:2a²+6ab,
∴2a(a+3b)=2a²+6ab.
(3)含a,b的代数恒等式:(a+2b)(a+b)=a²+3ab+2b².几何图形如图
(2)所示.

(本题答案不唯一)

6核心素养运算能力[2025广西南宁期中,较难]
(1)填空并观察下列各式的规律:
$(a-b)(a+b)= $____;
$(a-b)(a^{2}+ab+b^{2})= a^{3}-b^{3};$
$(a-b)(a^{3}+a^{2}b+ab^{2}+b^{3})= a^{4}-b^{4};$
$(a-b)(a^{4}+a^{3}b+a^{2}b^{2}+ab^{3}+b^{4})= a^{5}-b^{5};$
……
可得到$(a-b)(a^{2024}+a^{2023}b+... +ab^{2023}+b^{2024})= $____;
(2)猜想:$(a-b)(a^{n-1}+a^{n-2}b+... +ab^{n-2}+b^{n-1})= $____(其中n为正整数,且$n≥2$);
(3)利用(2)中猜想的结论计算:$3^{7}-3^{6}+... -3^{2}+3.$

答案： [解]
(1)(a−b)(a+b)=a²−ab+ab−b²=a²−b².观察规律可得(a−b)(a²⁰²⁴+a²⁰²³b+...+ab²⁰²³+b²⁰²⁴)=a²⁰²⁵−b²⁰²⁵,故答案为a²−b²,a²⁰²⁵−b²⁰²⁵.
(2)根据
(1)中规律可得(a−b)(aⁿ⁻¹+aⁿ⁻²b+…+abⁿ⁻²+bⁿ⁻¹)=aⁿ−bⁿ,故答案为aⁿ−bⁿ.
(3)设
(2)中式子中的a=3,b=−1,n=8,则有[3−(−1)][3⁷+3⁶·(−1)+…+3·(−1)⁶+(−1)⁷]=3⁸−(−1)⁸,即4×(3⁷−3⁶+...+3−1)=3⁸−1,
∴3⁷−3⁶+...−3²+3−1=$\frac{3^{8}-1}{4}$，
∴3⁷−3⁶+...−3²+3=$\frac{3^{8}-1}{4}$+1=$\frac{3^{8}+3}{4}$.