《2025年初中必刷题八年级数学上册华师大版》

5 [2024湖南长沙浏阳期末,中]将完全平方公式$(a\pm b)^{2}= a^{2}\pm 2ab+b^{2}$进行适当地变形,可以解决很多的数学问题,例如:若$a+b= 3,ab= 1$,求$a^{2}+b^{2}$的值.解:$\because a+b= 3,\therefore (a+b)^{2}= 9$,即$a^{2}+2ab+b^{2}= 9$.又$\because ab= 1,\therefore a^{2}+b^{2}= 7$.
根据上面的解题思路与方法,解决下列问题:
(1)若$m+n= 7,m^{2}+n^{2}= 40$,求mn的值;
(2)若$m-n= 8,mn= 9$,求$m^{2}+n^{2}$的值;
(3)两个正方形ABCD,AEFG如图摆放,面积和为34,$BG= 8$,求图中阴影部分的面积.

答案：
(1)$\because m+n=7$，$\therefore(m+n)^2=49$，即$m^2+2mn+n^2=49$.$\because m^2+n^2=40$，$\therefore2mn=9$，即$mn=\frac{9}{2}$.
(2)$\because m-n=8$，$\therefore(m-n)^2=64$，即$m^2-2mn+n^2=64$.$\because mn=9$，$\therefore m^2+n^2=82$.
(3)设正方形$ABCD$，$AEFG$的边长分别为$x,y(x＞y)$.$\because$正方形$ABCD$，$AEFG$的面积和为34，$\therefore x^2+y^2=34$.$\because BG=8$，$\therefore x+y=8$.$\therefore(x+y)^2=64$,$即x^2+2xy+y^2=64$.$\because x^2+y^2=34$,$\therefore2xy=30$,$\therefore(x-y)^2=x^2-2xy+y^2=34-30=4$.$\because x＞y$,$\therefore x-y=2$,$\therefore\begin{cases}x+y=8,\\x-y=2,\end{cases}$解得$\begin{cases}x=5,\\y=3,\end{cases}$$\therefore$阴影部分的面积为$\frac{1}{2}×(x-y)x=5$.答:阴影部分的面积为5.

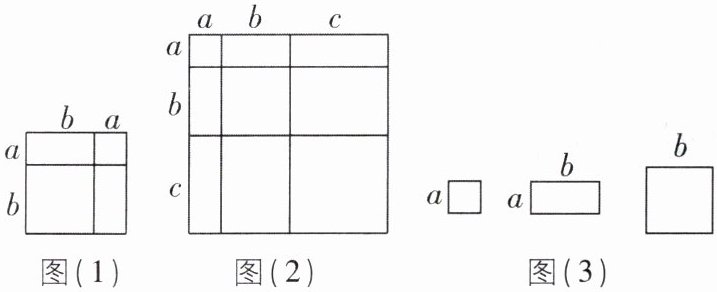
6 [2024河南南阳期中,中]对于一个图形,通过两种不同的方法计算它们的面积,可以得到一个数学等式,例如由图(1)可以得到$(a+b)^{2}= a^{2}+2ab+b^{2}$,请解答下列问题:
(1)类比图(1)的数学等式,写出图(2)表示的数学等式;
(2)若$a+b+c= 10,ab+ac+bc= 33$,用上面得到的数学等式求$a^{2}+b^{2}+c^{2}$的值;
(3)小明同学用图(3)中的x张边长为a的正方形,y张边长为b的正方形,z张宽为a、长为b的长方形拼出一个面积为$(a+7b)(9a+4b)$的长方形,求$x+y+z$的值.

答案：
(1)题图
(2)表示数学等式为$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$.
(2)由
(1)的结论可得$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$.$\because a+b+c=10$,$ab+ac+bc=33$,$\therefore a^2+b^2+c^2=(a+b+c)^2-2ab-2ac-2bc=100-66=34$.
(3)由题可知,所拼图形的面积为$xa^2+yb^2+zab$.$\because(a+7b)(9a+4b)=9a^2+4ab+63ab+28b^2=9a^2+67ab+28b^2$,$\therefore x=9$,$y=28$,$z=67$,$\therefore x+y+z=104$.

7 [2024北京东城区校级期中,中]阅读材料:
我们已经学习过完全平方公式$a^{2}\pm 2ab+b^{2}= (a\pm b)^{2}$.对于多项式$x^{2}+2x+2$,虽然不能写成某个代数式的平方形式,但是可以写成$x^{2}+2x+1+1= (x+1)^{2}+1$,即一个含x的代数式的平方与另一个数的和的形式.更一般的,对于二次项系数不为1的二次三项式$ax^{2}+bx+c(a≠0)$,它总是可以化为$a(x+h)^{2}+k$的形式,我们把这种代数式的恒等变形叫做配方.例如:$2x^{2}+4x-3= 2(x^{2}+2x+1)-5= 2(x+1)^{2}-5$,这就是一个配方的过程.根据以上内容回答下列问题:
(1)将代数式$x^{2}-4x+1$配方;
(2)已知$4a^{2}+4(a-b)+b^{2}+5= 0$,那么ab的值为______.

答案：
(1)$x^2-4x+1=x^2-4x+2^2-2^2+1=(x-2)^2-3$.
(2)$\because4a^2+4(a-b)+b^2+5=0$,$\therefore4a^2+4a+1+b^2-4b+4=0$,$\therefore(2a+1)^2+(b-2)^2=0$,$\therefore2a+1=0$,$b-2=0$,解得$a=-\frac{1}{2}$,$b=2$,$\therefore ab=-\frac{1}{2}×2=-1$.故答案为-1.