第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2024重庆巫溪期末]如图,点P是∠AOB的平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为点C,点D,下列结论不一定成立的是( )
A.∠1 = ∠2
B.PC = PD
C.∠3 = ∠4
D.OP = 2PC
A.∠1 = ∠2
B.PC = PD
C.∠3 = ∠4
D.OP = 2PC
答案:
1.D [解析]
∵点P是∠AOB的平分线上的一点,
∴∠1=∠2,故A正确;
∵PC⊥OA,PD⊥OB,
∴PC=PD,故B正确;在Rt△OCP和Rt△ODP中,{OP=OP,PC=PD},
∴Rt△OCP≌Rt△ODP,
∴OC=OD,∠3=∠4,故C正确;OP=2PC无法证明.故选D.
∵点P是∠AOB的平分线上的一点,
∴∠1=∠2,故A正确;
∵PC⊥OA,PD⊥OB,
∴PC=PD,故B正确;在Rt△OCP和Rt△ODP中,{OP=OP,PC=PD},
∴Rt△OCP≌Rt△ODP,
∴OC=OD,∠3=∠4,故C正确;OP=2PC无法证明.故选D.
2 [2025江苏扬州高邮期中]如图,在△ABC中,∠C = 90°,D是边BC上一点,且AD平分∠BAC,若CD = 3,AB = 10,则△ABD的面积是( )
A.12
B.15
C.30
D.无法确定
A.12
B.15
C.30
D.无法确定
答案:
2.B [解析]如图,过D作DH⊥AB于H.
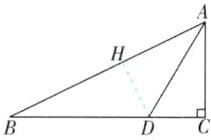
∵∠C=90°,
∴DC⊥AC.
又
∵AD平分∠BAC,
∴DH=DC=3.
∵AB=10,
∴△ABD的面积为$\frac{1}{2}$AB·DH=$\frac{1}{2}$×10×3=15.故选B.
2.B [解析]如图,过D作DH⊥AB于H.

∵∠C=90°,
∴DC⊥AC.
又
∵AD平分∠BAC,
∴DH=DC=3.
∵AB=10,
∴△ABD的面积为$\frac{1}{2}$AB·DH=$\frac{1}{2}$×10×3=15.故选B.
3 [2025陕西西安新城区质检]如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线交于点O,则S_{△ABO} : S_{△BCO} : S_{△CAO}等于( )
A.1 : 1 : 1
B.1 : 2 : 3
C.2 : 3 : 4
D.3 : 4 : 5
A.1 : 1 : 1
B.1 : 2 : 3
C.2 : 3 : 4
D.3 : 4 : 5
答案:
3.C [解析]如图,过点O分别作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,则OE=OF=OD,
∴S△ABO:S△BCO:S△CAO=($\frac{1}{2}$·AB·OE):($\frac{1}{2}$·BC·OF):($\frac{1}{2}$·AC·OD)=AB:BC:AC=2:3:4,故选C.

3.C [解析]如图,过点O分别作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,则OE=OF=OD,
∴S△ABO:S△BCO:S△CAO=($\frac{1}{2}$·AB·OE):($\frac{1}{2}$·BC·OF):($\frac{1}{2}$·AC·OD)=AB:BC:AC=2:3:4,故选C.

4 如图,AD // BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE = 3,则AD与BC间的距离为______。
答案:
4.6 [解析]如图,过点P作PF⊥AD于F,作PG⊥BC于G.
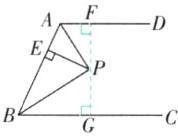
∵AP是∠BAD的平分线,PE⊥AB,
∴PF=PE,同理可得PG=PE.
∵AD//BC,
∴F,P,G三点共线,
∴FG的长即为AD,BC间的距离,
∴平行线AD与BC间的距离为3+3=6,故答案为6.
4.6 [解析]如图,过点P作PF⊥AD于F,作PG⊥BC于G.

∵AP是∠BAD的平分线,PE⊥AB,
∴PF=PE,同理可得PG=PE.
∵AD//BC,
∴F,P,G三点共线,
∴FG的长即为AD,BC间的距离,
∴平行线AD与BC间的距离为3+3=6,故答案为6.
5 如图,直线$l_1,l_2,l_3$表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址共有( )

A.一处
B.两处
C.三处
D.四处

A.一处
B.两处
C.三处
D.四处
答案:
5.D [解析]如图,可选择的地址有四处.故选D.

5.D [解析]如图,可选择的地址有四处.故选D.

6 [2025辽宁大连期中]小明将两把完全相同的长方形直尺按如图所示方式放置在∠AOB上,两把直尺的接触点为P,边OA与其中一把直尺的一边重合,与另一把直尺的一边交于点C,点C,P在这把直尺上对应的刻度分别是2,5,则OC的长度是______。
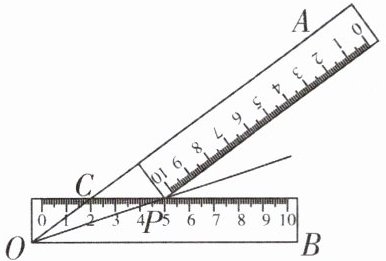

答案:
6.3 [解析]如图,过P作PN⊥OB于N.由题意得点P到OA,OB的距离相等,
∴OP平分∠AOB,
∴∠COP=∠NOP.
∵PC//OB,
∴∠CPO=∠NOP,
∴∠COP=∠CPO,
∴OC=PC.又
∵点C,P在这把直尺上对应的刻度分别是2,5,
∴PC=5−2=3,
∴OC的长度是3.
故答案为3.

6.3 [解析]如图,过P作PN⊥OB于N.由题意得点P到OA,OB的距离相等,
∴OP平分∠AOB,
∴∠COP=∠NOP.
∵PC//OB,
∴∠CPO=∠NOP,
∴∠COP=∠CPO,
∴OC=PC.又
∵点C,P在这把直尺上对应的刻度分别是2,5,
∴PC=5−2=3,
∴OC的长度是3.
故答案为3.

7 如图,已知BE⊥AC于E,CF⊥AB于F,BE,CF相交于点D,若AB = AC。求证:AD平分∠BAC。


答案:
7.[证明]如图,连结BC.
∵BE⊥AC于E,CF⊥AB于F,
∴∠CFB=∠BEC=90°.
关键点拨:利用平行线间等判定点为△ABC三条内角平分线的交点是解题的关键。
关键点拨:由题意得到OP平分∠AOB是解题关键。
另解:先证△AFC≌△AEB,得到AE=AF,再用HL证明Rt△AFD≌Rt△AED,得到∠FAD=∠EAD,所以AD平分∠BAC.
∵AB=AC,
∴∠ABC=∠ACB.
在△BCF和△CBE中,
∵{∠BFC=∠CEB,∠FBC=∠ECB,BC=BC},
∴△BCF≌△CBE(AAS),
∴BF=CE.
在△BFD和△CED中,
∵{∠BFD=∠CED,∠FDB=∠EDC,BF=CE},
∴△BFD≌△CED(AAS),
∴DF=DE,
∴AD平分∠BAC.

7.[证明]如图,连结BC.
∵BE⊥AC于E,CF⊥AB于F,
∴∠CFB=∠BEC=90°.
关键点拨:利用平行线间等判定点为△ABC三条内角平分线的交点是解题的关键。
关键点拨:由题意得到OP平分∠AOB是解题关键。
另解:先证△AFC≌△AEB,得到AE=AF,再用HL证明Rt△AFD≌Rt△AED,得到∠FAD=∠EAD,所以AD平分∠BAC.
∵AB=AC,
∴∠ABC=∠ACB.
在△BCF和△CBE中,
∵{∠BFC=∠CEB,∠FBC=∠ECB,BC=BC},
∴△BCF≌△CBE(AAS),
∴BF=CE.
在△BFD和△CED中,
∵{∠BFD=∠CED,∠FDB=∠EDC,BF=CE},
∴△BFD≌△CED(AAS),
∴DF=DE,
∴AD平分∠BAC.

8 如图,在△ABC中,∠ABC的平分线与外角∠ACE的平分线交于点P,PD⊥AC于点D,PH⊥BA于点H。
(1)若PH = 8 cm,求点P到直线BC的距离;
(2)求证:点P在∠HAC的平分线上。
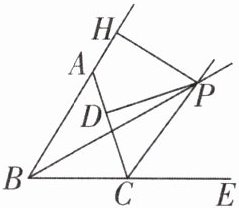
(1)若PH = 8 cm,求点P到直线BC的距离;
(2)求证:点P在∠HAC的平分线上。

答案:
8.
(1)[解]作PQ⊥BE于Q.
∵BP平分∠ABC,PH⊥BA,
∴PQ=PH=8cm,
即点P到直线BC的距离为8cm.
(2)[证明]
∵CP平分∠ACE,PQ⊥BE,PD⊥AC,
∴PD=PQ.又
∵PH=PQ,
∴PD=PH.
∵PD⊥AC,PH⊥BA,
∴点P在∠HAC的平分线上.
(1)[解]作PQ⊥BE于Q.
∵BP平分∠ABC,PH⊥BA,
∴PQ=PH=8cm,
即点P到直线BC的距离为8cm.
(2)[证明]
∵CP平分∠ACE,PQ⊥BE,PD⊥AC,
∴PD=PQ.又
∵PH=PQ,
∴PD=PH.
∵PD⊥AC,PH⊥BA,
∴点P在∠HAC的平分线上.
查看更多完整答案,请扫码查看


