第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
一、选择题(每小题3分,共27分)
1下列运算正确的是( )
A.$2a + 3b = 5ab$
B.$(a - b)^{2} = a^{2} - b^{2}$
C.$(ab^{2})^{3} = a^{3}b^{5}$
D.$3a^{3} \cdot (-4a^{2}) = -12a^{5}$
1下列运算正确的是( )
A.$2a + 3b = 5ab$
B.$(a - b)^{2} = a^{2} - b^{2}$
C.$(ab^{2})^{3} = a^{3}b^{5}$
D.$3a^{3} \cdot (-4a^{2}) = -12a^{5}$
答案:
D 【解析】2a和3b不是同类项,不能合并,故A选项错误,不符合题意;$(a - b)^{2}=a^{2}-2ab + b^{2}$,故B选项错误,不符合题意;$(ab^{2})^{3}=a^{3}b^{6}$,故C选项错误,不符合题意;$3a^{3}\cdot (-4a^{2})=-12a^{5}$,故D选项正确,符合题意.故选D.
2如果$m^{2} + m = 5$,那么代数式$m(m - 2) + (m + 2)^{2}$的值为( )
A.$14$
B.$9$
C.$-1$
D.$-6$
A.$14$
B.$9$
C.$-1$
D.$-6$
答案:
A 【解析】$m(m - 2)+(m + 2)^{2}=m^{2}-2m + m^{2}+4m + 4=2m^{2}+2m + 4$.当$m^{2}+m = 5$时,原式$=2(m^{2}+m)+4=2× 5+4=10 + 4=14$.故选A.
3下列计算正确的是( )
A.$10a^{4}b^{3}c^{2} ÷ 5a^{3}bc = ab^{2}c$
B.$(a^{2}bc)^{2} ÷ abc = a$
C.$(9x^{2}y - 6xy^{2}) ÷ 3xy = 3x - 2y$
D.$(6a^{2}b - 5a^{2}c) ÷ (-3a^{2}) = -2b - \frac{5}{3}c$
A.$10a^{4}b^{3}c^{2} ÷ 5a^{3}bc = ab^{2}c$
B.$(a^{2}bc)^{2} ÷ abc = a$
C.$(9x^{2}y - 6xy^{2}) ÷ 3xy = 3x - 2y$
D.$(6a^{2}b - 5a^{2}c) ÷ (-3a^{2}) = -2b - \frac{5}{3}c$
答案:
C 【解析】A选项,$10a^{4}b^{3}c^{2}÷ 5a^{3}bc=2ab^{2}c$,故此选项错误;B选项,$(a^{2}bc)^{2}÷ abc=a^{4}b^{2}c^{2}÷ abc=a^{3}bc$,故此选项错误;C选项,$(9x^{2}y - 6xy^{2})÷ 3xy=3x - 2y$,故此选项正确;D选项,$(6a^{2}b - 5a^{2}c)÷ (-3a^{2})=-2b+\frac {5}{3}c$,故此选项错误.故选C.
4[2025河南新乡期末]观察如图所示的两个多项式相乘的运算过程,根据你发现的规律分析,若$(x + a)(x + b) = x^{2} - 9x + 14$,则$a$,$b$的值可能分别是( )
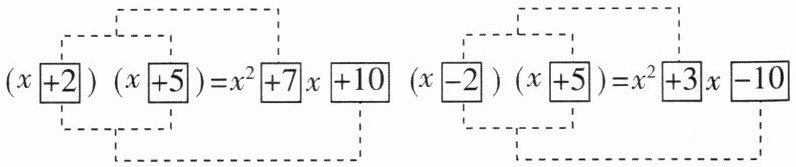
A.$-2$,$-7$
B.$-2$,$7$
C.$2$,$-7$
D.$2$,$7$
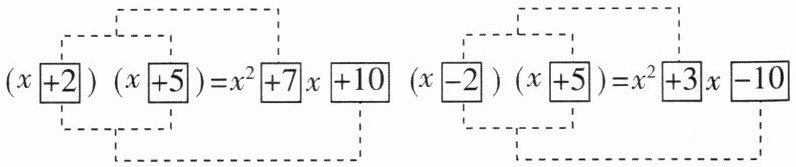
A.$-2$,$-7$
B.$-2$,$7$
C.$2$,$-7$
D.$2$,$7$
答案:
A 【解析】根据题意,知$a + b=-9,ab = 14$,
∴a,b的值可能分别是 - 2,-7,故选A.
∴a,b的值可能分别是 - 2,-7,故选A.
5[2024山东菏泽鄄城期末]在边长为$a的正方形中剪去一个边长为b的小正方形(a > b$,如图(1)),把余下部分沿虚线剪开拼成一个长方形(如图(2)),根据两个图形中阴影部分的面积相等,可以验证公式( )
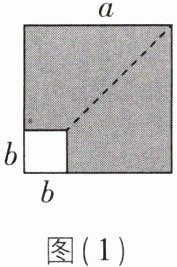

A.$(a + b)^{2} = a^{2} + 2ab + b^{2}$
B.$(a - b)^{2} = a^{2} - 2ab + b^{2}$
C.$(a + b)(a - b) = a^{2} - b^{2}$
D.$a(a - b) = a^{2} - ab$


A.$(a + b)^{2} = a^{2} + 2ab + b^{2}$
B.$(a - b)^{2} = a^{2} - 2ab + b^{2}$
C.$(a + b)(a - b) = a^{2} - b^{2}$
D.$a(a - b) = a^{2} - ab$
答案:
C 【解析】题图
(1)中阴影部分的面积为两个正方形的面积差,即$a^{2}-b^{2}$,题图
(2)中阴影部分图形拼成的是长为$a + b$,宽为$a - b$的长方形,因此其面积为$(a + b)(a - b)$,所以$a^{2}-b^{2}=(a + b)(a - b)$,即$(a + b)(a - b)=a^{2}-b^{2}$,故选C.

C 【解析】题图
(1)中阴影部分的面积为两个正方形的面积差,即$a^{2}-b^{2}$,题图
(2)中阴影部分图形拼成的是长为$a + b$,宽为$a - b$的长方形,因此其面积为$(a + b)(a - b)$,所以$a^{2}-b^{2}=(a + b)(a - b)$,即$(a + b)(a - b)=a^{2}-b^{2}$,故选C.


6已知$x^{a} = 3$,$x^{b} = 5$,则$x^{2a - 3b} = $ ( )
A.$\frac{9}{125}$
B.$\frac{22}{25}$
C.$\frac{3}{5}$
D.$15$
A.$\frac{9}{125}$
B.$\frac{22}{25}$
C.$\frac{3}{5}$
D.$15$
答案:
A 【解析】$\because x^{a}=3,x^{b}=5,\therefore x^{2a - 3b}=x^{2a}÷ x^{3b}=(x^{a})^{2}÷ (x^{b})^{3}=3^{2}÷ 5^{3}=\frac {9}{125}$.故选A.
7[2025上海杨浦区期中]已知$(x - 2021)^{2} + (x - 2025)^{2} = 34$,则$(x - 2023)^{2}$的值是( )
A.$5$
B.$9$
C.$13$
D.$17$
A.$5$
B.$9$
C.$13$
D.$17$
答案:
C 【解析】令$t = x - 2023$,则原式可化为$(t + 2)^{2}+(t - 2)^{2}=34$,则$t^{2}-4t + 4 + t^{2}+4t + 4 = 34$,解得$t^{2}=13$,即$(x - 2023)^{2}=13$.故选C.
8不论$x$,$y$为任何有理数,$x^{2} + y^{2} - 2x + 4y + 6$的值均为( )
A.正数
B.零
C.负数
D.非负数
A.正数
B.零
C.负数
D.非负数
答案:
A 【解析】原式$=x^{2}-2x + 1 + y^{2}+4y + 4 + 1=(x - 1)^{2}+(y + 2)^{2}+1$.因为$(x - 1)^{2}\geq 0,(y + 2)^{2}\geq 0$,所以$(x - 1)^{2}+(y + 2)^{2}+1\geq 1$.
9如图,将两张长为$a$,宽为$b$的长方形纸片按图(1),图(2)两种方式放置,图(1)和图(2)中两张长方形纸片重叠部分分别记为①和②,正方形$ABCD$中未被这两张长方形纸片覆盖部分用阴影表示,图(1)和图(2)中阴影部分的面积分别记为$S_{1}和S_{2}$.若知道下列条件,仍不能求$S_{1} - S_{2}$的值的是( )
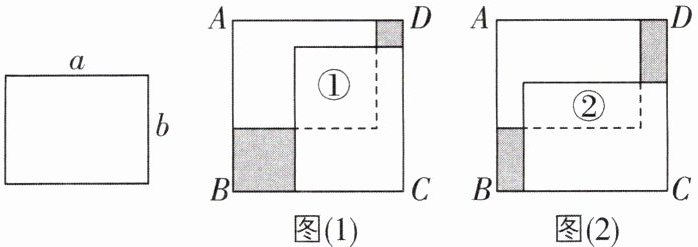
A.长方形纸片长和宽的差
B.长方形纸片的周长和面积
C.①和②的面积差
D.长方形纸片和①的面积差

A.长方形纸片长和宽的差
B.长方形纸片的周长和面积
C.①和②的面积差
D.长方形纸片和①的面积差
答案:
D 【解析】如图
(2),设阴影部分小长方形的宽、长分别为x,y,则图
(1)中阴影部分是边长分别为x,y的正方形,$a + x = b + y,\therefore a - b = y - x,\therefore S_{1}=x^{2}+y^{2},S_{2}=2xy,\therefore S_{1}-S_{2}=x^{2}+y^{2}-2xy=(x - y)^{2}=(a - b)^{2}=(a + b)^{2}-4ab$.长方形的面积是ab,长方形的周长是$2(a + b)$,故选项A、B正确;①的面积是$(b - x)(a - y)$,②的面积是$(a - x)(b - y),\therefore$①与②的面积差为$(b - x)(a - y)-(a - x)(b - y)=(a - b)(y - x)=(a - b)^{2}$,故C正确;选项D无法推出.故选D.
(2),设阴影部分小长方形的宽、长分别为x,y,则图
(1)中阴影部分是边长分别为x,y的正方形,$a + x = b + y,\therefore a - b = y - x,\therefore S_{1}=x^{2}+y^{2},S_{2}=2xy,\therefore S_{1}-S_{2}=x^{2}+y^{2}-2xy=(x - y)^{2}=(a - b)^{2}=(a + b)^{2}-4ab$.长方形的面积是ab,长方形的周长是$2(a + b)$,故选项A、B正确;①的面积是$(b - x)(a - y)$,②的面积是$(a - x)(b - y),\therefore$①与②的面积差为$(b - x)(a - y)-(a - x)(b - y)=(a - b)(y - x)=(a - b)^{2}$,故C正确;选项D无法推出.故选D.
二、填空题(每小题3分,共15分)
10[2025山东东营质检]因式分解:$2a^{3} - 8a = $______.
10[2025山东东营质检]因式分解:$2a^{3} - 8a = $______.
答案:
$2a(a + 2)(a - 2)$ 【解析】$2a^{3}-8a=2a(a^{2}-4)=2a(a + 2)(a - 2)$.
11[2025广东佛山南海区期末]老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
$÷ (-\frac{1}{2}y) = -6x + 2y - 1$,则手掌捂住的多项式为______.
$÷ (-\frac{1}{2}y) = -6x + 2y - 1$,则手掌捂住的多项式为______.
答案:
$3xy - y^{2}+\frac {1}{2}y$ 【解析】由题意得$(-6x + 2y - 1)\cdot (-\frac {1}{2}y)=-6x\cdot (-\frac {1}{2}y)+2y\cdot (-\frac {1}{2}y)-1\cdot (-\frac {1}{2}y)=3xy - y^{2}+\frac {1}{2}y$.故答案为$3xy - y^{2}+\frac {1}{2}y$.
12若$3^{a} \cdot 3^{b} = 27$,$(3^{a})^{b} = 3$,则$a^{2} + b^{2} = $______.
答案:
7 【解析】$\because 3^{a}\cdot 3^{b}=3^{a + b}=27 = 3^{3},\therefore a + b = 3.\because (3^{a})^{b}=3,\therefore ab = 1,\therefore a^{2}+b^{2}=(a + b)^{2}-2ab=3^{2}-2=7$.故答案为7.
13已知$M = (x - 2) \cdot (x - 6)$,$N = (x - 4)^{2}$,则$M与N$的大小关系是______.
答案:
$M\lt N$ 【解析】$\because M=(x - 2)(x - 6)=x^{2}-6x - 2x + 12=x^{2}-8x + 12,N=(x - 4)^{2}=x^{2}-8x + 16,\therefore M - N=(x^{2}-8x + 12)-(x^{2}-8x + 16)=-4\lt 0,\therefore M\lt N$.故答案为$M\lt N$.
14若$(x^{2} + mx + 4) \cdot (x^{2} - 3x + n)展开后不含x^{3}项和x$项,则$m + n$的值为______.
答案:
7 【解析】$(x^{2}+mx + 4)(x^{2}-3x + n)=x^{4}-3x^{3}+nx^{2}+mx^{3}-3mx^{2}+mnx + x^{2}-12x + 4n=x^{4}+(-3 + m)x^{3}+(n - 3m + 4)x^{2}+(mn - 12)x + n$.
∵$(x^{2}+mx + 4)(x^{2}-3x + n)$展开后不含$x^{3}$项和x项,$\therefore -3 + m = 0,mn - 12 = 0$,解得$m = 3,n = 4$,则$m + n = 3 + 4 = 7$.故答案为7.
∵$(x^{2}+mx + 4)(x^{2}-3x + n)$展开后不含$x^{3}$项和x项,$\therefore -3 + m = 0,mn - 12 = 0$,解得$m = 3,n = 4$,则$m + n = 3 + 4 = 7$.故答案为7.
查看更多完整答案,请扫码查看


