《2025年初中必刷题八年级数学上册华师大版》

1 [2024 河北邢台期末]下列计算正确的是( )

A.$(2a + b)^2 = 4a^2 + b^2$
B.$(5x - 2y)^2 = 25x^2 - 10xy + 4y^2$
C.$(\frac{1}{2}x - y)^2 = \frac{1}{2}x^2 - xy + y^2$
D.$(\frac{1}{2}x - \frac{1}{3})^2 = \frac{1}{4}x^2 - \frac{1}{3}x + \frac{1}{9}$

答案： 1.D　[解析]A选项，$(2a+b)^{2}=4a^{2}+4ab+b^{2}$，原计算错误，故此选项不符合题意;B选项，$(5x−2y)^{2}=25x^{2}-20xy + 4y^{2}$，原计算错误，故此选项不符合题意;C选项，$\left(\frac{1}{2}x - y\right)^{2}=\frac{1}{4}x^{2}-xy + y^{2}$，原计算错误，故此选项不符合题意;D选项，原计算正确，故此选项符合题意,故选D.

2 [2024 四川达州通川区期末]已知$x^2 + y^2 = 4$,$xy = 2$,那么$(x + y)^2$的值为 ( )

A.6
B.8
C.10
D.12

答案： 2.B　[解析]$(x + y)^{2}=x^{2}+2xy + y^{2}$，
∵$x^{2}+y^{2}=4$，$xy = 2$，
∴$(x + y)^{2}=4 + 2×2=4 + 4 = 8$.故选B.

3 计算：
(1) $(-4x - \frac{1}{2}y)^2$。
(2) $(2a - 1)^2 - (-3a + 1)(1 + 3a)$。
(3) $(2x - 2)(x + 1) - (x - 1)^2 - (x + 1)^2$。
(4) $(x + \frac{1}{4}y)^2 - (x - \frac{1}{4}y)^2$。

答案： 3.[解]
(1)原式$=\left(4x+\frac{1}{2}y\right)^{2}=16x^{2}+4xy+\frac{1}{4}y^{2}$.
(2)原式$=4a^{2}-4a + 1 + 9a^{2}-1=13a^{2}-4a$.
(3)原式$=2x^{2}+2x - 2x - 2-(x^{2}-2x + 1)-(x^{2}+2x + 1)=2x^{2}+2x - 2x - 2 - x^{2}+2x - 1 - x^{2}-2x - 1=-4$.
(4)原式$=\left(x^{2}+\frac{1}{2}xy+\frac{1}{16}y^{2}\right)-\left(x^{2}-\frac{1}{2}xy+\frac{1}{16}y^{2}\right)=x^{2}+\frac{1}{2}xy+\frac{1}{16}y^{2}-x^{2}+\frac{1}{2}xy-\frac{1}{16}y^{2}=xy$.

4 [2024 北京大兴区期末]已知$x + y = 5$,$xy = 6$,则$x^2 + y^2 = $ ( )

A.1
B.7
C.13
D.25

答案： 4.C　[解析]
∵$x + y = 5$，$xy = 6$，
∴$x^{2}+y^{2}=(x + y)^{2}-2xy=5^{2}-2×6 = 13$，故选C.

5 [2025 安徽芜湖期末]如图所示,将四个大小相同的小正方形按如图所示的方式放入一个边长为$a$的大正方形中,根据图中阴影部分的面积,可以验证的等式为 ( )

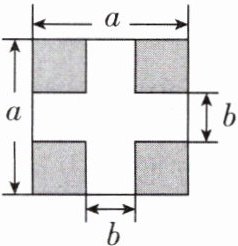
A.$(a - b)^2 = a^2 - 2ab + b^2$
B.$(a + b)^2 = a^2 + 2ab + b^2$
C.$(a - b)^2 = (a + b)^2 - 4ab$
D.$(a + b)(a - b) = a^2 - b^2$

答案： 5.A　[解析]由题图可得四个阴影小正方形可以拼成一个边长为$a - b$的正方形，因此阴影部分的面积可以表示为$(a - b)^{2}$.阴影部分的面积还等于大正方形的面积减去空白部分的面积，即$a^{2}-2ab + b^{2}$，因此可以验证的等式为$(a - b)^{2}=a^{2}-2ab + b^{2}$，故选A.

6 [2025 广东汕头潮南区期末]若$x + y = 2$,$x^2 + y^2 = 4$,则$x^{2024} + y^{2024}$的值是 ( )

A.4
B.$2024^2$
C.$2^{2024}$
D.$4^{2024}$

答案： 6.C　[解析]
∵$x + y = 2$，
∴$(x + y)^{2}=2^{2}=4$，
∴$x^{2}+2xy + y^{2}=4$.又
∵$x^{2}+y^{2}=4$，
∴$2xy = 0$，
∴$x$，$y$中有一个为0.不妨设$x = 0$，则$y = 2$，
∴$x^{2024}+y^{2024}=0^{2024}+2^{2024}=2^{2024}$，故选C.

7 [2024 上海徐汇区期中]已知$x^2 - 5x + 1 = 0$,则$(x - \frac{1}{x})^2 = $______。

答案： 7.21　[解析]
∵$x^{2}-5x + 1 = 0$，当$x = 0$时，等式不成立，
∴$x\neq0$，
∴$x - 5+\frac{1}{x}=0$，
∴$x+\frac{1}{x}=5$，
∴$\left(x-\frac{1}{x}\right)^{2}=\left(x+\frac{1}{x}\right)^{2}-4x\cdot\frac{1}{x}=5^{2}-4×1 = 21$.故答案为21.

8 [2024 河北邢台期末]已知$a - b = -4$,$ab = 3$,求$a^2 + b^2$的值。悦悦的解法如下：
解：因为$a - b = -4$,$ab = 3$,所以$a^2 + b^2 = (a - b)^2 + 2ab = (-4)^2 + 2×3 = 22$。
请你根据上述解题思路解答下面问题：
(1)已知$a - b = 7$,$ab = -12$,求$a^2 + b^2 - ab$的值；
(2)已知$(2023 - x)(2022 - x) = 20$,求$(2023 - x)^2 + (2022 - x)^2$的值。

答案： 8.[解]
(1)
∵$a - b = 7$，$ab = - 12$，
∴$a^{2}+b^{2}-ab=(a - b)^{2}+ab=7^{2}-12 = 37$.
(2)
∵$(2023 - x)(2022 - x)=20$，
∴$(2023 - x)^{2}+(2022 - x)^{2}=[(2023 - x)-(2022 - x)]^{2}+2(2023 - x)(2022 - x)=1^{2}+2(2023 - x)(2022 - x)=1 + 2×20 = 41$.

9 计算$(-a - b)^2$等于 ( )

A.$a^2 - 2ab + b^2$
B.$a^2 + 2ab + b^2$
C.$a^2 + b^2$
D.$a^2 - b^2$

答案： 9.B 【解析】原式$=[-(a+b)]^{2}=(a+b)^{2}=a^{2}+2ab+b^{2}$，故选 B.