《2025年初中必刷题八年级数学上册华师大版》

1[2025河北石家庄质检,中]五根小木棒的长度(单位:cm)分别为8,9,12,15,17,现将它们摆成两个直角三角形,其中正确的是 ( )

答案： C 【解析】A选项,9² + 12²≠17²,8² + 12²≠15²,故本选项不正确;B选项,9² + 12²≠17²,8² + 15²=17²,故本选项不正确;C选项,9² + 12²=15²,8² + 15²=17²,故本选项正确;D选项,9² + 8²≠12²,12² + 15²≠17²,故本选项不正确.故选C.

2[2025重庆渝北区期中,中]如图,在$\triangle ABC$中,$AB= \sqrt {180}$,$AC= 12$,$BC= 6$,将$\triangle ABC$折叠,得到折痕DE,且顶点B恰好与点A重合,点C落在点F处,则CE的长为 ( )

A.4
B.$\frac {9}{2}$
C.5
D.$3\sqrt {10}$

答案：
B 【解析】连结BE,如图.
∵AB= $\sqrt{180}$,AC=12,BC=6,
∴AB²=180,AC²=144,BC²=36,
∴AB²=AC² + BC²,
∴△ABC是直角三角形,且∠C=90°.由折叠的性质得,DE⊥AB.
∵顶点B恰好与点A重合,
∴BD=AD,
∴DE是AB的垂直平分线,
∴BE=AE.设CE=x,则BE=AE=12 - x.在Rt△BCE中,BE²=CE² + BC²,
∴(12 - x)²=x² + 6²,
∴x= $\frac{9}{2}$,
∴CE= $\frac{9}{2}$.故选B.
思路分析
过点O作OE⊥AC于E,OF⊥BC于F,OD⊥AB于D.先证明△ABC为直角三角形,再根据角平分线的性质得到OE=OF=OD,设OE=x,然后利用S△ABC=S△OAB + S△OAC + S△OCB得到关于x的方程,从而可得到OF的长度.
思路分析
连结BE,先证明△ABC是直角三角形,且∠C=90°,再证明DE是AB的垂直平分线,得到BE=AE,设CE=x,则BE=AE=12 - x,利用勾股定理列方程即可求解.

3[中]已知等腰直角三角形ABC中,$∠ABC= 90^{\circ }$,$AB= BC= 4$,平面内有一点D,连结CD,AD,若$CD= 2$,$AD= 6$,则$∠BCD= $____.

答案：
135°或45° 【解析】分两种情况讨论,如图
(1)和图
(2).
∵∠ABC=90°,AB=BC=4,
∴AC²=4² + 4²=32.又
∵CD²=4,AD²=6²=36,
∴AD²=AC² + CD²,
∴△ACD为直角三角形,∠ACD=90°.
∵△ABC为等腰直角三角形,
∴∠ACB=45°.故①∠BCD=90° + 45°=135°;②∠BCD=90° -45°=45°.综上,∠BCD=135°或45°.

4[2025河南商丘期末,中]如图,在$\triangle ABC$中,$AB= 5$,$BC= 4$,$AC= 3$,点O是$\triangle ABC$三条角平分线的交点,则$\triangle BCO$的边BC上的高是____.

答案：
1【解析】过O作OE⊥AC于E,OF⊥BC于F,OD⊥AB于D,如图.
∵在△ABC中,AB=5,BC=4,AC=3,
∴BC² + AC²=4² + 3²=25,AB²=5²=25,
∴BC² + AC²=AB²,
∴△ABC是直角三角形,且∠ACB=90°.
∵点O为△ABC三条角平分线的交点,
∴OE=OF=OD.设OE=OF=OD=x.
∵S△OAB + S△OAC + S△OBC=S△ABC,
∴ $\frac{1}{2}$ ×5×OD + $\frac{1}{2}$ ×3×OE + $\frac{1}{2}$ ×4×OF= $\frac{1}{2}$ ×4×3,
∴5x + 3x + 4x=12,解得x=1,
∴点O到BC的距离等于1,即△BCO的边BC上的高是1.

5[较难]在如图所示的正方形网格中,每个小正方形的边长均为1,点A,B,C,D,E均是网格线的交点,则$∠ACB-∠DCE= $____$^{\circ }$.

答案：
45 【解析】如图,标出点F,G,连结CG,AG.由勾股定理得AG²=CG²=1² + 2²=5,AC²=1² + 3²=10,则AG² + CG²=AC²,所以∠CGA=90°,即△CAG是等腰直角三角形,所以∠CAG=45°.因为AF//BC,所以∠CAF=∠BCA.在△AFG和△CDE中,{AF=CD,∠AFG=∠CDE=90°,FG=DE,所以△AFG≌△CDE(SAS),所以∠FAG=∠DCE,所以∠ACB - ∠DCE=∠CAF - ∠FAG=∠CAG=45°.故答案为45.

6[2025吉林长春期末,中]如图,$\triangle ACD和\triangle BCE$是两个等腰直角三角形,$∠ACD= ∠ECB= 90^{\circ }$,连结AE,DE.若有$AE^{2}= DE^{2}+2CE^{2}$,求$∠DEC$的度数.

答案：
【解】当点E在△ACD外时,连结DB,如图
(1).
∵△ACD和△ECB都是等腰直角三角形,∠ACD=∠ECB=90°,
∴AC=CD,CE=CB,∠ACE=∠DCB=90° + ∠ACB.在△ACE和△DCB中,{AC=CD,∠ACE=∠DCB,CE=CB,
∴△ACE≌△DCB,
∴AE=BD.
∵△BCE是等腰直角三角形,∠BCE=90°,
∴∠BEC=∠EBC=45°.在Rt△BCE中,CE² + CB²=BE²,
∴BE²=2CE².
∵AE²=DE² + 2CE²,
∴AE²=DE² + BE²,
∴BD²=DE² + BE²,
∴∠BED=90°,
∴∠DEC=∠BED - ∠BEC=90° - 45°=45°.
当点E在△ACD内时,连结BD,如图
(2).同理可得△ACE≌△DCB,
∴AE=BD.
∵△BCE是等腰直角三角形,∠BCE=90°,
∴BE²=2CE².又
∵AE²=DE² + 2CE²,
∴BD²=DE² + BE²,
∴∠BED=90°.又
∵∠BEC=45°,
∴∠DEC=∠BED + ∠BEC=90° + 45°=135°.
综上所述,∠DEC的度数为45°或135°.

7核心素养模型观念[2025河南平顶山期末,中]
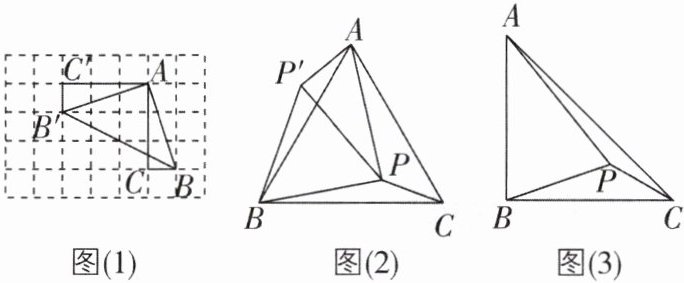
(1)如图(1),在正方形网格中,$\triangle ABC$的三个顶点都在小正方形的顶点上,把$\triangle ABC$绕点A顺时针旋转$90^{\circ }$,得到$\triangle AB'C'$,连结$BB'$,则$∠AB'B= $____.
(2)如图(2),在等边三角形ABC内有一点P,且$PA= 2$,$PB= \sqrt {3}$,$PC= 1$,若把$\triangle BPC$绕点B逆时针旋转$60^{\circ }得到\triangle BP'A$,连结$PP'$,求$∠BPC的度数和PP'$的长.
(3)如图(3),在等腰直角三角形ABC内有一点P,且$∠ABC= 90^{\circ }$,$PA= 6$,$PB= 4$,$PC= 2$,求$∠BPC$的度数.

答案：
【解】
(1)
∵将△ABC绕点A顺时针旋转90°得到△AB'C',
∴AB=AB',∠B'AB=90°,
∴∠AB'B=45°,故答案为45°.
(2)
∵△ABC是等边三角形,
∴∠ABC=60°.
∵将△BPC绕点B逆时针旋转60°得到△BP'A,
∴AP'=CP=1,BP'=BP= $\sqrt{3}$,∠PBC=∠P'BA,∠AP'B=∠BPC,∠PBP'=60°,
∴△BPP'是等边三角形,
∴PP'= $\sqrt{3}$,∠BP'P=60°.
∵AP'=1,AP=2,
∴AP'² + PP'²=1² + ( $\sqrt{3}$ )²=4,AP²=2²=4,
∴AP'² + PP'²=AP²,
∴△PP'A是直角三角形,且∠AP'P=90°,
∴∠BPC=∠AP'B=∠AP'P + ∠BP'P=90° + 60°=150°.
(3)如图,将△BPC绕点B逆时针旋转90°,得到△BP'A,连结PP',则BP'=BP=4,∠PBP'=90°,
∴PP'= $\sqrt{BP'² + BP²}$ = $\sqrt{32}$,∠BP'P=∠BPP'=45°.
∵PA=6,P'P= $\sqrt{32}$,PC=AP'=2,
∴P'A² + PP'²=PA²,
∴△PP'A是直角三角形,且∠AP'P=90°,
∴∠BPC=∠AP'B=∠AP'P + ∠BP'P=90° + 45°=135°.