第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 下列三角形中,不是等腰三角形的是( )
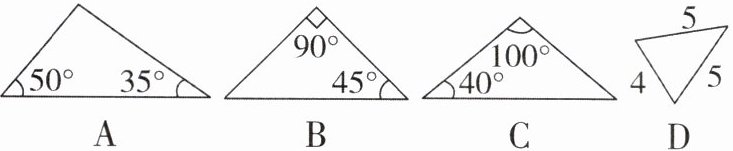

答案:
A【解析】
∵第三个角的大小为180° - 50° - 35° = 95°,
∴A选项中的三角形不是等腰三角形;
∵第三个角的大小为180° - 90° - 45° = 45°,
∴B选项中的三角形是等腰三角形;
∵第三个角的大小为180° - 100° - 40° = 40°,
∴C选项中的三角形是等腰三角形;
∵三角形中有两边长均为5,
∴选项D中的三角形是等腰三角形。
∵第三个角的大小为180° - 50° - 35° = 95°,
∴A选项中的三角形不是等腰三角形;
∵第三个角的大小为180° - 90° - 45° = 45°,
∴B选项中的三角形是等腰三角形;
∵第三个角的大小为180° - 100° - 40° = 40°,
∴C选项中的三角形是等腰三角形;
∵三角形中有两边长均为5,
∴选项D中的三角形是等腰三角形。
2 [2025湖南长沙期中]如图,在△ABC中,∠ABC,∠ACB的平分线交于点D,过点D作EF//BC交AB于点E,交AC于点F.若AB= 12,AC= 8,则△AEF的周长是( )
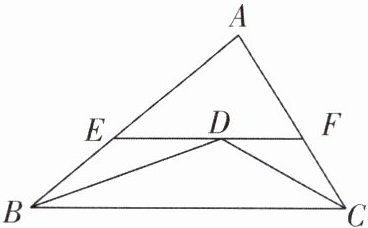
A.17
B.18
C.20
D.22

A.17
B.18
C.20
D.22
答案:
C【解析】
∵EF//BC,
∴∠EDB = ∠DBC。
∵BD平分∠ABC,
∴∠EBD = ∠DBC,
∴∠EDB = ∠EBD,
∴ED = EB。同理可得DF = FC,
∴△AEF的周长为AE + AF + EF = AE + AF + ED + DF = AE + BE + AF + CF = AB + AC = 20。故选C。
∵EF//BC,
∴∠EDB = ∠DBC。
∵BD平分∠ABC,
∴∠EBD = ∠DBC,
∴∠EDB = ∠EBD,
∴ED = EB。同理可得DF = FC,
∴△AEF的周长为AE + AF + EF = AE + AF + ED + DF = AE + BE + AF + CF = AB + AC = 20。故选C。
3 [2025山东枣庄滕州期末]如图,在△ABC中,AB= AC,点M在CA的延长线上,过点M作MN⊥BC于点N,交AB于点O,若AO= 3,BO= 4,则MC的长度为( )
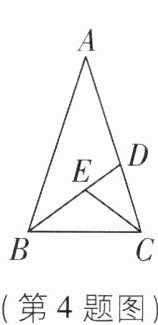
A.12
B.9
C.10
D.11

A.12
B.9
C.10
D.11
答案:
C【解析】
∵AB = AC,
∴∠B = ∠C。
∵MN⊥BC,
∴∠MNC = ∠MNB = 90°,
∴∠B + ∠BON = 90°,∠C + ∠M = 90°,
∴∠M = ∠BON。
∵∠BON = ∠MOA,
∴∠M = ∠MOA,
∴AM = AO = 3。
∵BO = 4,
∴AB = AC = AO + BO = 7,
∴MC = AM + AC = 10,故选C。
∵AB = AC,
∴∠B = ∠C。
∵MN⊥BC,
∴∠MNC = ∠MNB = 90°,
∴∠B + ∠BON = 90°,∠C + ∠M = 90°,
∴∠M = ∠BON。
∵∠BON = ∠MOA,
∴∠M = ∠MOA,
∴AM = AO = 3。
∵BO = 4,
∴AB = AC = AO + BO = 7,
∴MC = AM + AC = 10,故选C。
4 如图,在△ABC中,AB= AC,∠A= 36°,BD平分∠ABC交AC于点D,CE平分∠BCD交BD于点E,则图中等腰三角形的个数为______.
答案:
5【解析】
∵AB = AC,
∴△ABC是等腰三角形。
∵∠A = 36°,
∴∠ACB = ∠ABC = 72°。
∵BD平分∠ABC,
∴∠ABD = ∠DBC = 36°。
∵∠A = ∠ABD = 36°,
∴△ABD是等腰三角形。
∵∠BDC = ∠A + ∠ABD = 72° = ∠ACB,
∴BD = BC,
∴△BDC是等腰三角形。
∵CE平分∠BCD,
∴∠BCE = ∠DCE = 36°。
∵∠EBC = ∠BCE = 36°,
∴CE = BE,
∴△BCE是等腰三角形。
∵∠DEC = ∠EBC + ∠ECB = 72° = ∠EDC,
∴CD = CE,
∴△CDE是等腰三角形,
∴共有5个等腰三角形。故答案为5。
∵AB = AC,
∴△ABC是等腰三角形。
∵∠A = 36°,
∴∠ACB = ∠ABC = 72°。
∵BD平分∠ABC,
∴∠ABD = ∠DBC = 36°。
∵∠A = ∠ABD = 36°,
∴△ABD是等腰三角形。
∵∠BDC = ∠A + ∠ABD = 72° = ∠ACB,
∴BD = BC,
∴△BDC是等腰三角形。
∵CE平分∠BCD,
∴∠BCE = ∠DCE = 36°。
∵∠EBC = ∠BCE = 36°,
∴CE = BE,
∴△BCE是等腰三角形。
∵∠DEC = ∠EBC + ∠ECB = 72° = ∠EDC,
∴CD = CE,
∴△CDE是等腰三角形,
∴共有5个等腰三角形。故答案为5。
5 [2024云南大理鹤庆期中]如图,在△ABC中,AC= BC,D为边AB的中点,E为BC延长线上的一点,过点E作EF⊥AB,垂足为F,交AC于点G.求证:
(1)EF//CD;
(2)△CEG是等腰三角形.
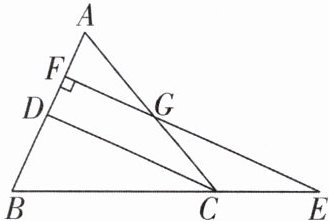

(1)EF//CD;
(2)△CEG是等腰三角形.


答案:
【证明】
(1)
∵AC = BC,D为边AB的中点,
∴CD⊥AB。
∵EF⊥AB,
∴EF//CD。
(2)
∵AC = BC,D为边AB的中点,
∴∠ACD = ∠BCD。
∵EF//CD,
∴∠ACD = ∠EGC,∠BCD = ∠E,
∴∠EGC = ∠E,
∴CG = CE,
∴△CEG是等腰三角形。
(1)
∵AC = BC,D为边AB的中点,
∴CD⊥AB。
∵EF⊥AB,
∴EF//CD。
(2)
∵AC = BC,D为边AB的中点,
∴∠ACD = ∠BCD。
∵EF//CD,
∴∠ACD = ∠EGC,∠BCD = ∠E,
∴∠EGC = ∠E,
∴CG = CE,
∴△CEG是等腰三角形。
6 [2024安徽蚌埠固镇期末]下列三角形中,不是等边三角形的是( )
A.有两个角是60°的三角形
B.有一个角是60°的等腰三角形
C.有两个角相等的等腰三角形
D.腰长和底边长相等的等腰三角形
A.有两个角是60°的三角形
B.有一个角是60°的等腰三角形
C.有两个角相等的等腰三角形
D.腰长和底边长相等的等腰三角形
答案:
C【解析】A选项,有两个角是60°的三角形,第三个角也是60°,故是等边三角形;B选项,有一个角是60°的等腰三角形是等边三角形;C选项,有两个角相等的等腰三角形,不一定是等边三角形;D选项,腰长和底边长相等的等腰三角形是等边三角形,故选C。
7 [2025广东云浮罗定期中]如图是某种落地灯的简易示意图,已知悬杆CD的长度与支杆BC的长度相等,且∠BCD= 60°.若CD的长度为40 cm,则此时B,D两点之间的距离为______cm.


答案:
40【解析】连结BD。
∵∠BCD = 60°,CD = BC,
∴△BCD为等边三角形,
∴CD = BD = 40cm,故答案为40。
∵∠BCD = 60°,CD = BC,
∴△BCD为等边三角形,
∴CD = BD = 40cm,故答案为40。
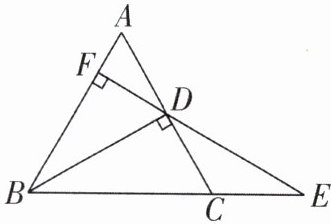
8 [2025河南南阳方城期末]如图,在△ABC中,点D是AC边的中点,BD⊥AC,点E在BC边的延长线上,连结ED并延长交AB于点F,且EF⊥AB,∠E= 30°.
(1)求证:△ABC是等边三角形;
(2)请判断线段AD与CE的数量关系,并说明理由.
(1)求证:△ABC是等边三角形;
(2)请判断线段AD与CE的数量关系,并说明理由.

答案:
(1)【证明】
∵BD⊥AC,点D是AC边的中点,
∴∠BDA = ∠BDC = 90°,AD = CD。又
∵BD = BD,
∴△BDA≌△BDC(SAS),
∴AB = CB。
∵EF⊥AB,
∴∠ABC + ∠E = 90°。
∵∠E = 30°,
∴∠ABC = 60°,
∴△ABC是等边三角形。
(2)【解】AD = CE。理由:
∵△ABC是等边三角形,
∴∠ACB = 60°。
∵∠ACB = ∠E + ∠CDE,∠E = 30°,
∴∠CDE = 30° = ∠E,
∴CD = CE。
∵点D是AC边的中点,
∴AD = CD,
∴AD = CE。
(1)【证明】
∵BD⊥AC,点D是AC边的中点,
∴∠BDA = ∠BDC = 90°,AD = CD。又
∵BD = BD,
∴△BDA≌△BDC(SAS),
∴AB = CB。
∵EF⊥AB,
∴∠ABC + ∠E = 90°。
∵∠E = 30°,
∴∠ABC = 60°,
∴△ABC是等边三角形。
(2)【解】AD = CE。理由:
∵△ABC是等边三角形,
∴∠ACB = 60°。
∵∠ACB = ∠E + ∠CDE,∠E = 30°,
∴∠CDE = 30° = ∠E,
∴CD = CE。
∵点D是AC边的中点,
∴AD = CD,
∴AD = CE。
查看更多完整答案,请扫码查看


