《2025年初中必刷题八年级数学上册华师大版》

1 [2024河南新乡期末，中]如图，小冰想用一条彩带缠绕圆柱4圈，正好从A点绕到正上方的B点，已知圆柱底面周长是3m，高为16m，则所需彩带最短是( )

A.8m
B.5m
C.20m
D.10m

答案：
C 【解析】如图，线段AB的长即为所需彩带最短的长度. 由图可知AC = 3×4 = 12(m)，BC = 16m，
∴由勾股定理得AB = $\sqrt{AC² + BC²}$ = $\sqrt{12² + 16²}$ = 20(m)，故选C.

2 勾股定理相传由西周初数学家商高发现，故又称“商高定理”.如图(1)，以直角三角形ABC的各边为边分别向外作正方形，再把较小的两个正方形按图(2)的方式放置在最大的正方形内，三块阴影区域面积分别记为S₁，S₂，S₃，两个较小正方形的重叠部分(六边形PQMNHG)的面积记为S₄，则S₁，S₂，S₃，S₄的关系为( )

A.S₁+S₂=S₃+S₄
B.S₁+S₃=S₂+S₄
C.S₁+S₂+S₃=S₄
D.S₁+S₂+S₃＜S₄

答案： C 【解析】设题图
(1)中最大正方形的面积为S₅，较小正方形的面积为S₆，最小正方形的面积为S₇，则由勾股定理易得S₅ = S₆ + S₇.
∵题图
(2)中大正方形内空白部分面积为S₆ + S₇ - S₄，
∴S₁ + S₂ + S₃ = S₅ - (S₆ + S₇ - S₄) = S₅ - (S₅ - S₄) = S₅ - S₅ + S₄ = S₄，即S₁ + S₂ + S₃ = S₄，故选C.

3 [2024浙江温州期中，中]如图(1)，跷跷板是常见的一种游戏.跷跷板一端着地时如图(2)，支柱OM⊥地面MN，OA=OB，PC为把手，且PC⊥AB于C，AC=40cm，OM=70cm.跷跷板可以绕点O转动，图(3)是跷跷板水平即EF//MN时的示意图，此时点A，C，D，B的对应点分别为点E，G，H，F，且恰有AE=AG.则跷跷板AB的长为______cm.

答案：
265 【解析】由题意得EG = AC = 40cm，OE = OA. 如图，过A作AQ⊥EG于Q.
∵AE = AG，
∴QE = QG = $\frac{1}{2}$EG = 20cm.
∵EF//MN，
∴AQ = OM = 70cm. 在Rt△AQO中，AQ² + QO² = AO²，
∴70² + (AO - 20)² = AO²，
∴AO = $\frac{265}{2}$ cm，
∴AB = 2OA = 265cm，故答案为265.

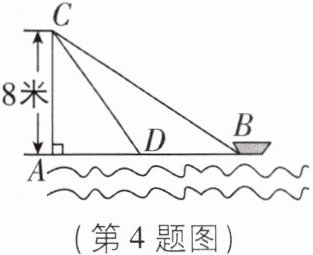
4 [中]如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为17米，几分钟后船到达点D的位置，此时绳子CD的长为10米，则船向岸边移动了______米.

答案： 9 【解析】在Rt△ABC中，
∵∠CAB = 90°，BC = 17米，AC = 8米，
∴AB = $\sqrt{BC² - AC²}$ = $\sqrt{17² - 8²}$ = 15(米). 在Rt△ACD中，
∵CD = 10米，
∴AD = $\sqrt{CD² - AC²}$ = $\sqrt{100 - 64}$ = 6(米)，
∴BD = AB - AD = 15 - 6 = 9(米)，则船向岸边移动了9米，故答案为9.

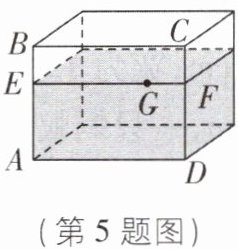
5 [中]如图所示的长方体透明玻璃鱼缸，假设其长AD=80cm，高AB=60cm，水深AE=40cm.在水面上紧贴内壁G处有一块面包屑，G在水面线EF上，且EG=60cm，一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处吃面包屑，则蚂蚁爬行的最短路线长为______cm.

答案：
100 【解析】如图所示，作点A关于BC的对称点A'，连结A'G交BC于点Q，蚂蚁沿着A→Q→G的路线爬行时路程最短，此时AQ + QG = A'Q + QG = A'G. 在Rt△A'EG中，A'E = 60 + (60 - 40) = 80(cm)，EG = 60cm，
∴A'G² = A'E² + EG² = 10000，
∴A'G = 100cm，
∴最短路线长为100cm. 故答案为100.

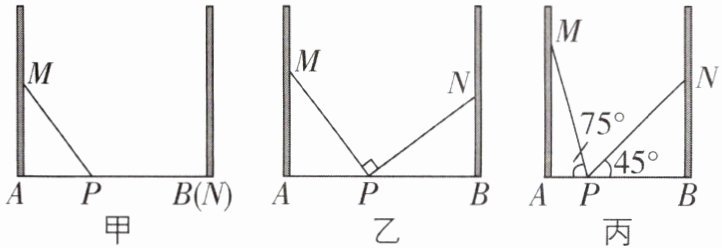
6 [2025江苏无锡新吴区期中，中]如图是小明家中的三个房间甲、乙、丙的截面图，他将一个梯子斜靠在墙上，梯子顶端距离地面的垂直距离记作MA，如果梯子的底端P不动，顶端靠在对面墙上，此时梯子的顶端距离地面的垂直距离记作NB.
(1)当小明在甲房间时，梯子靠在对面墙上，顶端刚好落在对面墙角B处，若MA=1.6米，AP=1.2米，则甲房间的宽度AB=______米.
(2)当他在乙房间时，测得MA=1.6米，NB=1.2米，且∠MPN=90°，求乙房间的宽AB；
(3)当他在丙房间时，测得MA=3.3米，且∠MPA=75°，∠NPB=45°，求丙房间的宽AB.

答案：
【解】
(1)在Rt△AMP中，
∵∠A = 90°，MA = 1.6米，AP = 1.2米，
∴PM = $\sqrt{AM² + AP²}$ = 2米.
∵PB = PM = 2米，
∴AB = AP + PB = 3.2米，故答案为3.2.
(2)
∵∠MPN = 90°，
∴∠APM + ∠BPN = 90°.
∵∠APM + ∠AMP = 90°，
∴∠AMP = ∠BPN. 在△AMP与△BPN中，{∠AMP = ∠BPN，∠MAP = ∠PBN = 90°，MP = PN，
∴△AMP≌△BPN，
∴MA = PB = 1.6米，AP = BN = 1.2米，
∴AB = AP + PB = 1.2 + 1.6 = 2.8(米).
(3)如图，过点N作MA的垂线，垂足为点D，连结NM，则DN//AB.设AB = x，则易知AB = ND = x.
∵∠NPB = 45°，DN//AB，
∴∠DNP = 45°.
∵PM = PN，∠MPN = 180° - 75° - 45° = 60°，
∴△PNM为等边三角形，
∴∠MNP = 60°，NM = PM，
∴∠MND = 15°.
∵∠APM = 75°，
∴∠AMP = 15°，
∴∠DNM = ∠AMP，
∴△AMP≌△DNM(AAS)，
∴AM = DN，
∴AB = DN = AM = 3.3米，即丙房间的宽AB是3.3米.