第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
8[2024山东泰安中考]如图,直线l//m,等边三角形ABC的两个顶点B,C分别落在直线l,m上,若∠ABE= 21°,则∠ACD的度数是( )
A.45°
B.39°
C.29°
D.21°
A.45°
B.39°
C.29°
D.21°
答案:
B 【解析】如图,过点 A作 AF//l.
∵ 直线 l//m,
∴ AF//m.
∵ △ABC 是等边三角形,
∴ ∠BAC=60°.
∵ AF//l,
∴ ∠BAF=∠ABE=21°,
∴ ∠CAF=∠BAC-∠BAF=60°-21°=39°.
∵ AF//m,
∴ ∠ACD=∠CAF=39°,故选 B.
∵ 直线 l//m,
∴ AF//m.
∵ △ABC 是等边三角形,
∴ ∠BAC=60°.
∵ AF//l,
∴ ∠BAF=∠ABE=21°,
∴ ∠CAF=∠BAC-∠BAF=60°-21°=39°.
∵ AF//m,
∴ ∠ACD=∠CAF=39°,故选 B.
9[2024广东广州中考]如图,在△ABC中,∠A= 90°,AB= AC= 6,D为边BC的中点,点E,F分别在边AB,AC上,AE= CF,则四边形AEDF的面积为( )
A.18
B.9√2
C.9
D.6√2
A.18
B.9√2
C.9
D.6√2
答案:
C 【解析】如图,连结 AD.
∵ ∠BAC=90°,AB=AC=6,D 为边 BC 的中点,
∴ AD=BD=CD,∠BAD=∠C=45°,S△ABC=1/2×6×6=18. 在△ADE 和△CDF 中,{AD=CD,∠BAD=∠C,AE=CF,
∴ △ADE≌△CDF(SAS),
∴ S△ADE=S△CDF,
∴ S四边形AEDF=S△AED+S△ADF=S△CDF+S△ADF=S△ADC=1/2S△ABC=9,故选 C.
∵ ∠BAC=90°,AB=AC=6,D 为边 BC 的中点,
∴ AD=BD=CD,∠BAD=∠C=45°,S△ABC=1/2×6×6=18. 在△ADE 和△CDF 中,{AD=CD,∠BAD=∠C,AE=CF,
∴ △ADE≌△CDF(SAS),
∴ S△ADE=S△CDF,
∴ S四边形AEDF=S△AED+S△ADF=S△CDF+S△ADF=S△ADC=1/2S△ABC=9,故选 C.
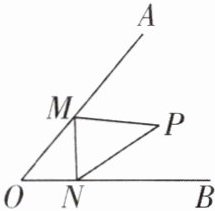
10[2024黑龙江绥化中考]如图,已知∠AOB= 50°,点P为∠AOB内部一点,点M为射线OA、点N为射线OB上的两个动点,当△PMN的周长最小时,则∠MPN= ______。

答案:
80° 【解析】如图,分别作 P 关于 OA,OB 的对称点 P₁,P₂,连结 OP₁,OP₂,P₁P₂. 当 M,N分别是 P₁P₂ 与 OA,OB 的交点时,△PMN 的周长最小.
∵ P,P₁ 关于 OA 对称,
∴ ∠P₁OP=2∠MOP,OP₁=OP,P₁M=PM,∠OP₁M=∠OPM,同理,∠P₂OP=2∠NOP,OP=OP₂,∠OP₂N=∠OPN,
∴ ∠P₁OP₂=∠P₁OP+∠P₂OP=2(∠MOP+∠NOP)=2∠AOB=100°,OP₁=OP₂=OP,
∴ △P₁OP₂是等腰三角形,
∴ ∠OP₂N=∠OP₁M=40°,
∴ ∠MPN=∠MPO+∠NPO=∠OP₁M+∠OP₂N=80°. 故答案为 80°.
∵ P,P₁ 关于 OA 对称,
∴ ∠P₁OP=2∠MOP,OP₁=OP,P₁M=PM,∠OP₁M=∠OPM,同理,∠P₂OP=2∠NOP,OP=OP₂,∠OP₂N=∠OPN,
∴ ∠P₁OP₂=∠P₁OP+∠P₂OP=2(∠MOP+∠NOP)=2∠AOB=100°,OP₁=OP₂=OP,
∴ △P₁OP₂是等腰三角形,
∴ ∠OP₂N=∠OP₁M=40°,
∴ ∠MPN=∠MPO+∠NPO=∠OP₁M+∠OP₂N=80°. 故答案为 80°.
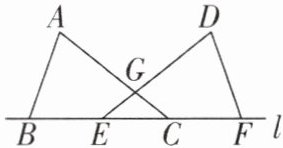
11[2024江苏常州中考]如图,B,E,C,F是直线l上的四点,AC,DE相交于点G,AB= DF,AC= DE,BC= EF。
(1)求证:△GEC是等腰三角形;
(2)连结AD,则AD与l的位置关系是______。
(1)求证:△GEC是等腰三角形;
(2)连结AD,则AD与l的位置关系是______。

答案:
(1)【证明】在△ABC 和△DFE 中,{AB=DF,AC=DE,BC=EF,
∴ △ABC≌△DFE,
∴ ∠ACB=∠DEF,
∴ EG=CG,即△GEC 是等腰三角形.(2)【解】
∵ AC=DE,EG=CG,
∴ AC-CG=DE-EG,
∴ AG=DG,
∴ ∠GAD=∠GDA=1/2(180°-∠AGD).
∵ ∠ACE=∠DEF=1/2(180°-∠CGE),∠AGD=∠EGC,
∴ ∠CAD=∠ACB,
∴ AD//l. 故答案为 AD//l.
∴ △ABC≌△DFE,
∴ ∠ACB=∠DEF,
∴ EG=CG,即△GEC 是等腰三角形.(2)【解】
∵ AC=DE,EG=CG,
∴ AC-CG=DE-EG,
∴ AG=DG,
∴ ∠GAD=∠GDA=1/2(180°-∠AGD).
∵ ∠ACE=∠DEF=1/2(180°-∠CGE),∠AGD=∠EGC,
∴ ∠CAD=∠ACB,
∴ AD//l. 故答案为 AD//l.
12[2024山东烟台中考]某班开展“用直尺和圆规作角平分线”的探究活动,各组展示作图痕迹如下,其中射线OP为∠AOB的平分线的有( )
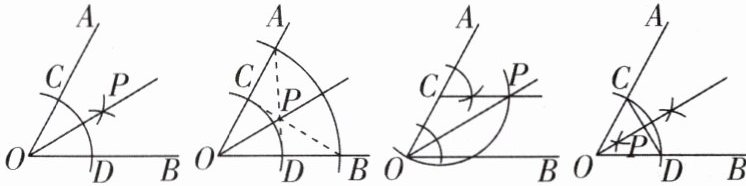
A.1个
B.2个
C.3个
D.4个
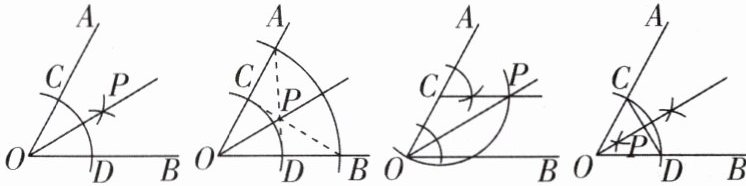
A.1个
B.2个
C.3个
D.4个
答案:
D 【解析】A 选项,由作图痕迹可知,射线 OP 为∠AOB 的平分线. B 选项,如图,由作图痕迹可知,OC=OD,OE=OF,
∴ CE=DF.又
∵ ∠AOD=∠BOC,
∴ △EDO≌△FCO(SAS),
∴ ∠CEP=∠DFP,
∴ 易证△ECP≌△FDP(AAS),
∴ EP=FP,
∴ 易得△EPO≌△FPO(SSS),
∴ ∠AOP=∠BOP,即射线 OP 为∠AOB 的平分线. C 选项,由作图痕迹可知,∠ACP=∠AOB,
∴ CP//OB,
∴ ∠CPO=∠POB. 又
∵ CP=OC,
∴ ∠COP=∠CPO,
∴ ∠POB=∠COP,即射线 OP 为∠AOB 的平分线. D 选项,由作图痕迹可知,CO=OD,OP 垂直平分 CD,则射线 OP 是∠AOB 的平分线. 故选 D.
∴ CE=DF.又
∵ ∠AOD=∠BOC,
∴ △EDO≌△FCO(SAS),
∴ ∠CEP=∠DFP,
∴ 易证△ECP≌△FDP(AAS),
∴ EP=FP,
∴ 易得△EPO≌△FPO(SSS),
∴ ∠AOP=∠BOP,即射线 OP 为∠AOB 的平分线. C 选项,由作图痕迹可知,∠ACP=∠AOB,
∴ CP//OB,
∴ ∠CPO=∠POB. 又
∵ CP=OC,
∴ ∠COP=∠CPO,
∴ ∠POB=∠COP,即射线 OP 为∠AOB 的平分线. D 选项,由作图痕迹可知,CO=OD,OP 垂直平分 CD,则射线 OP 是∠AOB 的平分线. 故选 D.
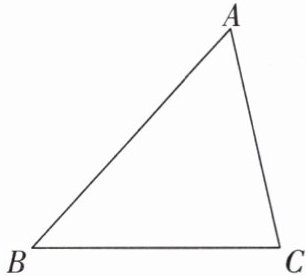
13[2023陕西中考]如图,已知锐角△ABC,∠B= 48°。请用尺规作图法,在△ABC内部求作一点P,使PB= PC,且∠PBC= 24°。(保留作图痕迹,不写作法)

答案:
【解】如图,点 P 即为所求.
14[2024四川绵阳中考]如图,在△ABC中,AB= 5,AD平分∠BAC交BC于点D,DE⊥AC,垂足为E,△ABD的面积为5,则DE的长为( )

A.1
B.2
C.3
D.5

A.1
B.2
C.3
D.5
答案:
B 【解析】过 D 作 DF⊥AB 于 F,如图.
∵ AD 平分∠BAC,DE⊥AC,DF⊥AB,
∴ DE=DF.
∵ △ABD的面积为 5,
∴ 1/2AB·DF=5. 又
∵ AB=5,
∴ DF=2,
∴ DE=2. 故选 B.
∵ AD 平分∠BAC,DE⊥AC,DF⊥AB,
∴ DE=DF.
∵ △ABD的面积为 5,
∴ 1/2AB·DF=5. 又
∵ AB=5,
∴ DF=2,
∴ DE=2. 故选 B.
15[2024湖南中考]如图,在锐角三角形ABC中,AD是边BC上的高,在BA,BC上分别截取线段BE,BF,使BE= BF;分别以点E,F为圆心,大于1/2EF的长为半径画弧,在∠ABC内,两弧交于点P,作射线BP,交AD于点M,过点M作MN⊥AB于点N。若MN= 2,AD= 4MD,则AM= ______。


答案:
6 【解析】由作图可知 BP 平分∠ABC.
∵ AD是边 BC 上的高,MN⊥AB,MN=2,
∴ MD=MN=2.
∵ AD=4MD,
∴ AD=8,
∴ AM=AD-MD=6,故答案为 6.
∵ AD是边 BC 上的高,MN⊥AB,MN=2,
∴ MD=MN=2.
∵ AD=4MD,
∴ AD=8,
∴ AM=AD-MD=6,故答案为 6.
查看更多完整答案,请扫码查看


