第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1[2025甘肃兰州质检]如图,在△ABC中,AB= AC,∠BAC= 130°,DA⊥AC,则∠ADB= ( )
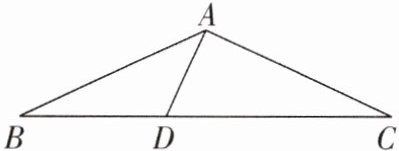
A.100°
B.115°
C.130°
D.145°

A.100°
B.115°
C.130°
D.145°
答案:
B 【解析】在△ABC 中,AB=AC,
∴∠B=∠C.
∵∠BAC=130°,
∴∠B=∠C= $\frac{180^{\circ}-130^{\circ}}{2}=25^{\circ}$.
∵DA⊥AC,
∴∠DAC=90°,
∴∠ADC=90°-25°=65°,
∴∠ADB=180°-∠ADC=180°-65°=115°,故选 B.
∴∠B=∠C.
∵∠BAC=130°,
∴∠B=∠C= $\frac{180^{\circ}-130^{\circ}}{2}=25^{\circ}$.
∵DA⊥AC,
∴∠DAC=90°,
∴∠ADC=90°-25°=65°,
∴∠ADB=180°-∠ADC=180°-65°=115°,故选 B.
2[2025广东广州期中]如图,在△ABC中,∠BAC= 100°,点D,E分别在边BC,AC上,且AB= AD= DE= EC,则∠ADE= ______.
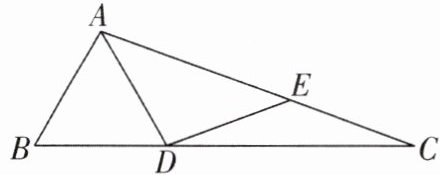

答案:
100° 【解析】设∠C=x.
∵ED=EC,
∴∠EDC=∠C=x,
∴∠DEA=∠C+∠EDC=2x.
∵DA=DE,
∴∠DAE=∠DEA=2x,
∴∠ADB=∠C+∠DAE=3x.
∵AB=AD,
∴∠B=∠ADB=3x.
∵∠BAC=100°,
∴∠B+∠C=180°-∠BAC=80°,
∴3x+x=80°,
∴x=20°,
∴∠C=∠EDC=20°,∠ADB=3x=60°,
∴∠ADE=180°-∠EDC-∠ADB=100°.故答案为 100°.
∵ED=EC,
∴∠EDC=∠C=x,
∴∠DEA=∠C+∠EDC=2x.
∵DA=DE,
∴∠DAE=∠DEA=2x,
∴∠ADB=∠C+∠DAE=3x.
∵AB=AD,
∴∠B=∠ADB=3x.
∵∠BAC=100°,
∴∠B+∠C=180°-∠BAC=80°,
∴3x+x=80°,
∴x=20°,
∴∠C=∠EDC=20°,∠ADB=3x=60°,
∴∠ADE=180°-∠EDC-∠ADB=100°.故答案为 100°.
3如图,E是△ABC外部的一点,连结AE,BE,CE.已知AB= AC,AD= AE,AD,AC分别是∠BAC,∠DAE的平分线,点B,D,E在同一直线上,∠BAD= 35°.
(1)求证:△ABD≌△ACE;
(2)求∠BEC的度数.
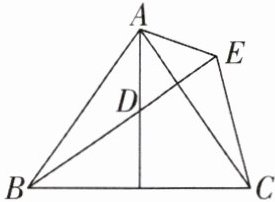
(1)求证:△ABD≌△ACE;
(2)求∠BEC的度数.

答案:
(1)【证明】
∵AD,AC 分别是∠BAC,∠DAE 的平分线,
∴∠BAD=∠CAD=∠CAE.
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS).
(2)【解】由(1)得,∠BAD=∠CAD=∠CAE=35°,
∴∠DAE=2∠CAE=70°.
∵AD=AE,
∴∠ADE=∠AED=$\frac{1}{2}(180^{\circ}-\angle DAE)=55^{\circ}$.
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵∠BAD+∠ABD=∠ADE=55°,
∴∠CAE+∠ACE=55°,
∴∠BEC=180°-(∠CAE+∠ACE)-∠AED=180°-55°-55°=70°.
∵AD,AC 分别是∠BAC,∠DAE 的平分线,
∴∠BAD=∠CAD=∠CAE.
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS).
(2)【解】由(1)得,∠BAD=∠CAD=∠CAE=35°,
∴∠DAE=2∠CAE=70°.
∵AD=AE,
∴∠ADE=∠AED=$\frac{1}{2}(180^{\circ}-\angle DAE)=55^{\circ}$.
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵∠BAD+∠ABD=∠ADE=55°,
∴∠CAE+∠ACE=55°,
∴∠BEC=180°-(∠CAE+∠ACE)-∠AED=180°-55°-55°=70°.
4[2025江苏盐城期中]如图,在△ABC中,AC= BC,∠A= 35°,观察图中尺规作图的痕迹,可知∠BCG的度数为( )
A.40°
B.45°
C.50°
D.55°
A.40°
B.45°
C.50°
D.55°
答案:
D 【解析】
∵AC=BC,∠A=35°,
∴∠A=∠B=35°,
∴∠ACB=180°-35°-35°=110°.由作图痕迹可知,CF⊥AB,
∴CF 平分∠ACB,
∴∠BCG=$\frac{1}{2}\angle ACB=55^{\circ}$,故选 D.
∵AC=BC,∠A=35°,
∴∠A=∠B=35°,
∴∠ACB=180°-35°-35°=110°.由作图痕迹可知,CF⊥AB,
∴CF 平分∠ACB,
∴∠BCG=$\frac{1}{2}\angle ACB=55^{\circ}$,故选 D.
5[2025浙江湖州期中]如图,在△ABC中,AB= AC,AD⊥BC于点D,E,F是AD上的两点.若BD= 2,AD= 3,则图中阴影部分的面积是______.
答案:
3 【解析】
∵在△ABC 中,AB=AC,AD⊥BC 于点 D,
∴BD=CD,
∴$S_{\triangle BEF}=\frac{1}{2}EF\cdot BD=\frac{1}{2}EF\cdot CD=S_{\triangle CEF}$.
∵BD=2,AD=3,
∴$S_{阴影部分}=S_{\triangle ABD}=\frac{1}{2}BD\cdot AD=\frac{1}{2}×2×3=3$,故答案为 3.
∵在△ABC 中,AB=AC,AD⊥BC 于点 D,
∴BD=CD,
∴$S_{\triangle BEF}=\frac{1}{2}EF\cdot BD=\frac{1}{2}EF\cdot CD=S_{\triangle CEF}$.
∵BD=2,AD=3,
∴$S_{阴影部分}=S_{\triangle ABD}=\frac{1}{2}BD\cdot AD=\frac{1}{2}×2×3=3$,故答案为 3.
6如图,在△ABC中,∠BAC= 90°,E为边BC上的点,且AB= AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF//BC,且AF,EF相交于点F.
(1)求证:∠C= ∠BAD;
(2)求证:AC= EF.
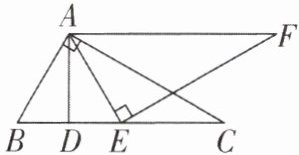
(1)求证:∠C= ∠BAD;
(2)求证:AC= EF.

答案:
(1)【证明】
∵AB=AE,D 为线段 BE 的中点,
∴AD⊥BC,
∴∠C+∠DAC=90°.
∵∠BAC=90°,
∴∠BAD+∠DAC=90°,
∴∠C=∠BAD.
(2)【证明】
∵AF//BC,
∴∠FAE=∠AEB.
∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠FAE.又∠AEF=∠BAC=90°,AB=AE,
∴△ABC≌△EAF(ASA),
∴AC=EF.
∵AB=AE,D 为线段 BE 的中点,
∴AD⊥BC,
∴∠C+∠DAC=90°.
∵∠BAC=90°,
∴∠BAD+∠DAC=90°,
∴∠C=∠BAD.
(2)【证明】
∵AF//BC,
∴∠FAE=∠AEB.
∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠FAE.又∠AEF=∠BAC=90°,AB=AE,
∴△ABC≌△EAF(ASA),
∴AC=EF.
7[2025四川泸州期末]等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角为( )
A.50°
B.130°
C.50°或130°
D.55°或130°
A.50°
B.130°
C.50°或130°
D.55°或130°
答案:
C 【解析】①如图
(1),等腰三角形 ABC 为锐角三角形,AB=AC,BD⊥AC,∠ABD=40°,
∴∠A=50°,即顶角的度数为 50°.②如图
(2),等腰三角形 ABC 为钝角三角形,AB=AC,BD⊥AC,∠DBA=40°,
∴∠BAD=50°,
∴∠BAC=130°即顶角的度数为 130°.故选 C.
(1),等腰三角形 ABC 为锐角三角形,AB=AC,BD⊥AC,∠ABD=40°,
∴∠A=50°,即顶角的度数为 50°.②如图
(2),等腰三角形 ABC 为钝角三角形,AB=AC,BD⊥AC,∠DBA=40°,
∴∠BAD=50°,
∴∠BAC=130°即顶角的度数为 130°.故选 C.
查看更多完整答案,请扫码查看


