第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [中]如图,$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle B = 30^{\circ}$,要求用圆规和直尺作图,把它分成两个三角形,其中至少有一个三角形是等腰三角形。其作法错误的是( )
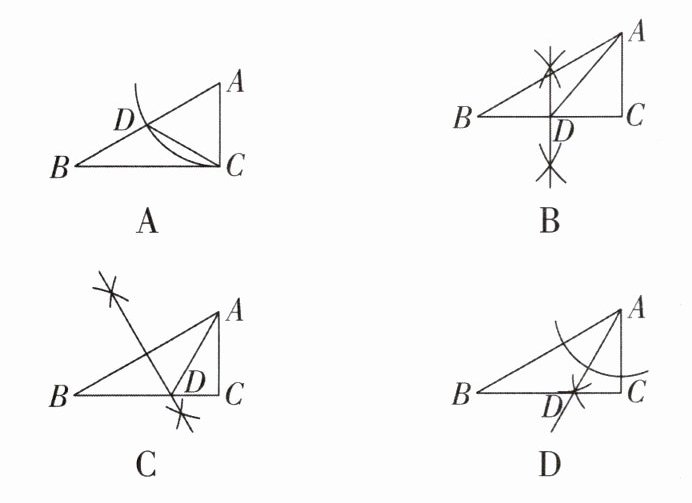
A.
B.
C.
D.

A.
B.
C.
D.
答案:
B [解析]A选项,由作法知AD=AC,
∴△ACD是等腰三角形.
∵在Rt△ABC中,∠B=30°,
∴∠A=60°,
∴△ACD是等边三角形,
∴∠ACD=60°,
∴∠BCD=30°,
∴∠BCD=∠B,
∴BD=CD,
∴△BCD是等腰三角形,故选项A不符合题意;B选项,由作法知所作图形是线段BC的垂直平分线,点D是BC的中点,不能推出△ACD或△ABD是等腰三角形,故选项B符合题意;C选项,由作法知,所作图形是线段AB的垂直平分线,
∴DA=DB,
∴△ABD是等腰三角形,故选项C不符合题意;D选项,∠C=90°,∠B=30°,
∴∠BAC=60°,由作法知AD是∠BAC的平分线,
∴∠BAD=30°=∠B,
∴DB=DA,
∴△ABD是等腰三角形,故选项D不符合题意.故选B.
∴△ACD是等腰三角形.
∵在Rt△ABC中,∠B=30°,
∴∠A=60°,
∴△ACD是等边三角形,
∴∠ACD=60°,
∴∠BCD=30°,
∴∠BCD=∠B,
∴BD=CD,
∴△BCD是等腰三角形,故选项A不符合题意;B选项,由作法知所作图形是线段BC的垂直平分线,点D是BC的中点,不能推出△ACD或△ABD是等腰三角形,故选项B符合题意;C选项,由作法知,所作图形是线段AB的垂直平分线,
∴DA=DB,
∴△ABD是等腰三角形,故选项C不符合题意;D选项,∠C=90°,∠B=30°,
∴∠BAC=60°,由作法知AD是∠BAC的平分线,
∴∠BAD=30°=∠B,
∴DB=DA,
∴△ABD是等腰三角形,故选项D不符合题意.故选B.
2 [2024重庆南川区期末,中]如图,$\triangle ABC$是等腰三角形,底边$BC的长为6$,面积是$30$,腰$AC的垂直平分线EF分别交AC$,$AB于点E$,$F$。若点$D为BC$边的中点,点$M为线段EF$上一动点,则$\triangle CDM$周长的最小值是( )
A.$11$
B.$13$
C.$18$
D.$24$
A.$11$
B.$13$
C.$18$
D.$24$
答案:
B [解析]连结AD,AM,如图.
∵△ABC是等腰三角形,点D是BC边的中点,BC=6,
∴AD⊥BC,CD=3,
∴S△ABC=$\frac{1}{2}$BC·AD=$\frac{1}{2}$×6×AD=30,解得AD=10.
∵EF是线段AC的垂直平分线,
∴CM=AM,
∴CD+CM+DM=CD+AM+DM.
∵AM+DM≥AD,
∴AD的长为CM+DM的最小值,
∴△CDM周长的最小值为AD+CD=10+3=13,故选B.

B [解析]连结AD,AM,如图.
∵△ABC是等腰三角形,点D是BC边的中点,BC=6,
∴AD⊥BC,CD=3,
∴S△ABC=$\frac{1}{2}$BC·AD=$\frac{1}{2}$×6×AD=30,解得AD=10.
∵EF是线段AC的垂直平分线,
∴CM=AM,
∴CD+CM+DM=CD+AM+DM.
∵AM+DM≥AD,
∴AD的长为CM+DM的最小值,
∴△CDM周长的最小值为AD+CD=10+3=13,故选B.

3 [2025江苏无锡质检,较难]如图,$\triangle ABC$中,$AB = AC$,$\angle BAC = 2\alpha$,$\angle BAC的平分线与AB的垂直平分线交于点O$,将$\angle C沿EF$($E在BC$上,$F在AC$上)折叠,若点$C与点O$恰好重合,则$\angle OEC$的度数为( )
A.$1.5\alpha$
B.$2\alpha$
C.$4\alpha$
D.$3\alpha$
A.$1.5\alpha$
B.$2\alpha$
C.$4\alpha$
D.$3\alpha$
答案:
C [解析]连结BO,CO,如图.
∵∠BAC=2α,∠BAC的平分线与AB的垂直平分线交于点O,
∴∠OAB=∠OAC=α,OA=OB,
∴∠OAB=∠ABO=α.
∵AB=AC,
∴∠ABC=∠ACB=$\frac{1}{2}$(180°−2α)=90°−α,
∴∠OBC=∠ABC−∠ABO=90°−2α.在△ABO和△ACO中,$\left\{\begin{array}{l}AB=AC,\\ \angle OAB=\angle OAC,\\ AO=AO,\end{array}\right.$
∴△ABO≌△ACO(SAS),
∴BO=CO,
∴∠OBC=∠OCB=90°−2α.由折叠可知EO=EC,
∴∠EOC=∠OCE=90°−2α,
∴∠OEC=180°−∠EOC−∠OCE=180°−2×(90°−2α)=4α,故选C.

C [解析]连结BO,CO,如图.
∵∠BAC=2α,∠BAC的平分线与AB的垂直平分线交于点O,
∴∠OAB=∠OAC=α,OA=OB,
∴∠OAB=∠ABO=α.
∵AB=AC,
∴∠ABC=∠ACB=$\frac{1}{2}$(180°−2α)=90°−α,
∴∠OBC=∠ABC−∠ABO=90°−2α.在△ABO和△ACO中,$\left\{\begin{array}{l}AB=AC,\\ \angle OAB=\angle OAC,\\ AO=AO,\end{array}\right.$
∴△ABO≌△ACO(SAS),
∴BO=CO,
∴∠OBC=∠OCB=90°−2α.由折叠可知EO=EC,
∴∠EOC=∠OCE=90°−2α,
∴∠OEC=180°−∠EOC−∠OCE=180°−2×(90°−2α)=4α,故选C.

4 [中]如图,已知$\triangle ABC三内角的平分线交于点D$,三边的垂直平分线交于点$E$,若$\angle BDC = 130^{\circ}$,则$\angle BEC = $____$^{\circ}$。
答案:
160 [解析]连结AE.
∵BD平分∠ABC,CD平分∠ACB,
∴∠DBC+∠DCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB.
∵∠BDC=130°,
∴∠DBC+∠DCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=180°−130°=50°,
∴∠ABC+∠ACB=100°,
∴∠BAC=80°.
∵AB,BC边的垂直平分线相交于点E,
∴AE=BE=CE,
∴∠BAE=∠ABE,∠EAC=∠ECA.
∵∠BAC=∠BAE+∠CAE=80°,
∴∠ABE+∠ECA=80°,
∴∠EBC+∠ECB=100°−80°=20°,
∴∠BEC=180°−20°=160°.故答案为160.
∵BD平分∠ABC,CD平分∠ACB,
∴∠DBC+∠DCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB.
∵∠BDC=130°,
∴∠DBC+∠DCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=180°−130°=50°,
∴∠ABC+∠ACB=100°,
∴∠BAC=80°.
∵AB,BC边的垂直平分线相交于点E,
∴AE=BE=CE,
∴∠BAE=∠ABE,∠EAC=∠ECA.
∵∠BAC=∠BAE+∠CAE=80°,
∴∠ABE+∠ECA=80°,
∴∠EBC+∠ECB=100°−80°=20°,
∴∠BEC=180°−20°=160°.故答案为160.
5 [2025重庆沙坪坝区质检,较难]如图,在$\triangle ABC$中,$AD \perp BC于点D$,过点$A作AE//BC$,且$AE = AB$,$AB上有一点F$,连结$EF$,若$\angle C = \angle AFE$,$CD = 4BD$,$S_{\triangle AEF} = 3$,则$S_{\triangle ABC} = $____。
答案:
5 [解析]在CD上取一点G,使得DG=BD,连结AG,过点E作EH⊥AB,交BA延长线于H,如图,
∴∠H=90°.
∵AD⊥BC,BD=DG,
∴AD垂直平分BG,
∴AB=AG,∠ADG=90°,
∴∠AGB=∠ABG.
∵AE//BC,
∴∠EAH=∠B,
∴∠EAH=∠AGB.
∵AE=AB,
∴AE=AG.在△EAH和△AGD中,$\left\{\begin{array}{l}\angle H=\angle ADG=90°,\\ \angle EAH=\angle AGB,\\ AE=AG,\end{array}\right.$
∴△EAH≌△AGD,
∴EH=AD,AH=DG.在△EHF和△ADC中,$\left\{\begin{array}{l}\angle EHF=\angle ADC=90°,\\ \angle EFA=\angle C,\\ EH=AD,\end{array}\right.$
∴△EHF≌△ADC,
∴FH=CD,
∴FH−AH=CD−GD,
∴AF=CG,
∴$\frac{1}{2}$AF·EH=$\frac{1}{2}$CG·AD,
∴S△AEF=S△AGC=3.设DG=BD=m,则CD=4BD=4m,
∴CG=4m−m=3m,BC=4m+m=5m,
∴$\frac{S_{\triangle ABC}}{S_{\triangle AGC}}$=$\frac{\frac{1}{2}BC·AD}{\frac{1}{2}CG·AD}$=$\frac{5m}{3m}$=$\frac{5}{3}$,
∴S△ABC=5.故答案为5.

5 [解析]在CD上取一点G,使得DG=BD,连结AG,过点E作EH⊥AB,交BA延长线于H,如图,
∴∠H=90°.
∵AD⊥BC,BD=DG,
∴AD垂直平分BG,
∴AB=AG,∠ADG=90°,
∴∠AGB=∠ABG.
∵AE//BC,
∴∠EAH=∠B,
∴∠EAH=∠AGB.
∵AE=AB,
∴AE=AG.在△EAH和△AGD中,$\left\{\begin{array}{l}\angle H=\angle ADG=90°,\\ \angle EAH=\angle AGB,\\ AE=AG,\end{array}\right.$
∴△EAH≌△AGD,
∴EH=AD,AH=DG.在△EHF和△ADC中,$\left\{\begin{array}{l}\angle EHF=\angle ADC=90°,\\ \angle EFA=\angle C,\\ EH=AD,\end{array}\right.$
∴△EHF≌△ADC,
∴FH=CD,
∴FH−AH=CD−GD,
∴AF=CG,
∴$\frac{1}{2}$AF·EH=$\frac{1}{2}$CG·AD,
∴S△AEF=S△AGC=3.设DG=BD=m,则CD=4BD=4m,
∴CG=4m−m=3m,BC=4m+m=5m,
∴$\frac{S_{\triangle ABC}}{S_{\triangle AGC}}$=$\frac{\frac{1}{2}BC·AD}{\frac{1}{2}CG·AD}$=$\frac{5m}{3m}$=$\frac{5}{3}$,
∴S△ABC=5.故答案为5.

6 [中]如图,在四边形$ABCD$中,$AD//BC$,$E为CD$的中点,连结$AE$,$BE$,$BE \perp AE$,延长$AE交BC的延长线于点F$。
求证:(1)$FC = AD$;(2)$AB = BC + AD$。
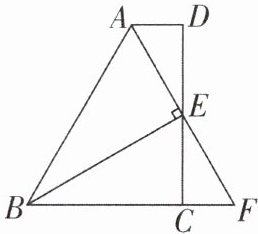
求证:(1)$FC = AD$;(2)$AB = BC + AD$。

答案:
(1)
∵AD//BC,
∴∠ADC=∠ECF.
∵E为CD的中点,
∴DE=EC.在△ADE与△FCE中,$\left\{\begin{array}{l}\angle ADE=\angle FCE,\\ DE=CE,\\ \angle AED=\angle FEC,\end{array}\right.$
∴△ADE≌△FCE(ASA),
∴FC=AD.
(2)由
(1)知△ADE≌△FCE,
∴AE=EF,AD=CF.
∵BE⊥AE,
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF.
∵AD=CF,
∴AB=BC+AD.
(1)
∵AD//BC,
∴∠ADC=∠ECF.
∵E为CD的中点,
∴DE=EC.在△ADE与△FCE中,$\left\{\begin{array}{l}\angle ADE=\angle FCE,\\ DE=CE,\\ \angle AED=\angle FEC,\end{array}\right.$
∴△ADE≌△FCE(ASA),
∴FC=AD.
(2)由
(1)知△ADE≌△FCE,
∴AE=EF,AD=CF.
∵BE⊥AE,
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF.
∵AD=CF,
∴AB=BC+AD.
7 核心素养逻辑推理[较难]在$\triangle ABC$中,$AB$,$AC的垂直平分线分别交BC于点E$,$F$。
(1)如图(1),当$\angle B = \angle C = 20^{\circ}$时,求$\angle EAF$的度数;
(2)如图(2),$AB \neq AC$,且$90^{\circ} < \angle BAC < 180^{\circ}$。
①若$\angle BAC = 130^{\circ}$,则$\angle EAF = $____$^{\circ}$;若$\angle BAC = n^{\circ}$,则$\angle EAF = $____;
②当$\angle BAC = $____$^{\circ}$时,$AE \perp AF$;
③若$BC = a$,求$\triangle AEF$的周长。(用含$a$的式子表示)
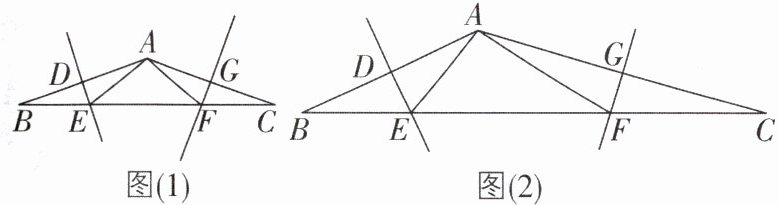
(1)如图(1),当$\angle B = \angle C = 20^{\circ}$时,求$\angle EAF$的度数;
(2)如图(2),$AB \neq AC$,且$90^{\circ} < \angle BAC < 180^{\circ}$。
①若$\angle BAC = 130^{\circ}$,则$\angle EAF = $____$^{\circ}$;若$\angle BAC = n^{\circ}$,则$\angle EAF = $____;
②当$\angle BAC = $____$^{\circ}$时,$AE \perp AF$;
③若$BC = a$,求$\triangle AEF$的周长。(用含$a$的式子表示)

答案:
(1)
∵DE垂直平分AB,GF垂直平分AC,
∴BE=AE,AF=CF,
∴∠B=∠BAE=20°,∠C=∠CAF=20°,
∴∠BAE+∠CAF=40°.
∵∠B=∠C=20°,
∴∠BAC=180°−∠B−∠C=140°,
∴∠EAF=∠BAC−(∠BAE+∠CAF)=140°−40°=100°.
(2)①80;2n°−180°
②135
③a
(1)
∵DE垂直平分AB,GF垂直平分AC,
∴BE=AE,AF=CF,
∴∠B=∠BAE=20°,∠C=∠CAF=20°,
∴∠BAE+∠CAF=40°.
∵∠B=∠C=20°,
∴∠BAC=180°−∠B−∠C=140°,
∴∠EAF=∠BAC−(∠BAE+∠CAF)=140°−40°=100°.
(2)①80;2n°−180°
②135
③a
查看更多完整答案,请扫码查看


