《2025年初中必刷题八年级数学上册华师大版》

1 [2025四川宜宾期末,中]如图,在正方形网格中,A,B两点都在小正方形的顶点上,如果点C也在图中小正方形的顶点上,且△ABC是等腰三角形,那么点C的个数为( )

A.1
B.2
C.3
D.4

答案：
C【解析】当AB为腰时，点C的个数为2，如图
(1)，图
(2)所示。

当AB为底时，点C的个数为1，如图
(3)。故选C。

2 [2025天津南开区期中,中]如图,在△ABC中,∠BAC= 90°,AB= AC= 6 cm,D为BC中点,E,F分别是AB,AC两边上的动点,且∠EDF= 90°,下列结论：①BE= AF；②EF的长度不变；③∠BED+∠CFD的度数不变；④四边形AEDF的面积为$9 cm^2.$其中正确结论的个数是( )

A.1
B.2
C.3
D.4

答案： C【解析】
∵AB = AC，∠BAC = 90°，D为BC中点，
∴AD⊥BC，∠BAD = ∠B = 45°，
∴AD = BD = DC。
∵∠BDA = ∠EDF = 90°，
∴∠BDE = ∠ADF。
∵∠B = ∠DAF = 45°，
∴△BDE≌△ADF(ASA)，
∴BE = AF，DE = DF，故①正确；
∵DE = DF，∠EDF = 90°，
∴△DEF是等腰直角三角形。
∵DE的长度是变化的，
∴EF的长度是变化的，故②错误；
∵△BDE≌△ADF，
∴∠BED = ∠AFD，
∴∠BED + ∠CFD = ∠AFD + ∠CFD = 180°，故③正确；
∵△BDE≌△ADF，
∴S△BDE = S△ADF，
∴S四边形AEDF = S△ADE + S△ADF = S△ADE + S△BDE = S△ADB = 1/2S△ABC = 1/2×1/2×6×6 = 9(cm²)，故④正确。故选C。

3 [2025江苏南京期中,中]如图,在△ABC中,D为BC边上一点,∠BAD= 30°,∠ACB= α,将△ABD沿AD翻折至△AB'D,连结CB',CB'平分∠ACB,则∠AB'D的度数是______.(用含α的代数式表示)

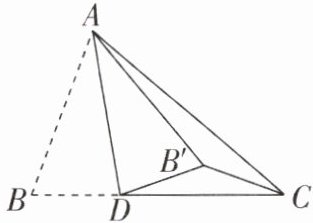
答案：
90° - 1/2α【解析】如图，连结BB'，过点B'作B'E⊥BC于E，B'F⊥AC于F，则∠CEB' = ∠CFB' = ∠BEB' = ∠AFB' = 90°。由翻折可知，∠BAD = ∠B'AD = 30°，AB = AB'，∠ABC = ∠AB'D，
∴∠BAB' = ∠BAD + ∠B'AD = 60°，
∴△ABB'是等边三角形，
∴AB' = BB'，∠B'BA = ∠B'AB = 60°。
∵CB'平分∠ACB，∠ACB = α，
∴∠ACB' = ∠BCB' = 1/2∠ACB = 1/2α。又
∵∠B'EC = ∠B'FC = 90°，B'C = B'C，
∴△B'EC≌△B'FC，
∴B'E = B'F。在Rt△BB'E和Rt△AB'F中，{B'E = B'F，BB' = AB'，
∴Rt△BB'E≌Rt△AB'F(HL)，
∴∠B'BE = ∠B'AF，
∴∠B'BA + ∠B'BE = ∠B'AB + ∠B'AF，即∠ABC = ∠BAC。
∵∠ACB = α，∠ABC + ∠BAC + ∠ACB = 180°，
∴∠ABC = ∠BAC = (180° - α)/2 = 90° - 1/2α，
∴∠AB'D = ∠ABC = 90° - 1/2α，故答案为90° - 1/2α。

4 [2025浙江嘉兴期中,中]如图,△ABC中,AB= AC,∠BAC= 100°,△AED是一个足够大的等腰直角三角形,∠AED= 90°,且可绕着点A旋转,边AE,AD分别交线段BC于Q,P两点.当∠PAC= ______时,△APQ为等腰三角形.

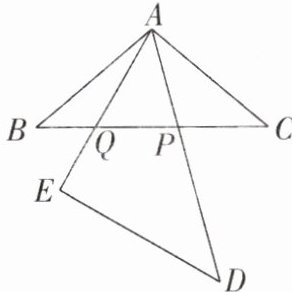
答案： 50°或5°或27.5°【解析】
∵AB = AC，∠BAC = 100°，
∴∠C = ∠B = 40°。
∵△AED是等腰直角三角形，∠AED = 90°，
∴∠DAE = 45°。当∠APQ = ∠AQP时，AP = AQ，∠APQ = 1/2×(180° - 45°) = 67.5°，
∴∠PAC = ∠APQ - ∠C = 67.5° - 40° = 27.5°。当∠PAQ = ∠AQP = 45°时，AP = PQ，∠APQ = 90°，
∴∠PAC = ∠APQ - ∠C = 90° - 40° = 50°。当∠PAQ = ∠APQ = 45°时，AQ = PQ，
∴∠PAC = ∠APQ - ∠C = 45° - 40° = 5°。综上所述，当∠PAC为50°或5°或27.5°时，△APQ为等腰三角形。故答案为50°或5°或27.5°。

5 [2025江苏南京期中,中]如图,点O是等边三角形ABC内一点,∠AOB= 110°,∠BOC= α,△ADC≌△BOC,连结OD.
(1)求证：△COD是等边三角形；
(2)当AO= AD时,α为多少?

答案：
(1)【证明】
∵△ABC是等边三角形，
∴∠ACB = 60°。
∵△ADC≌△BOC，
∴CD = CO，∠DCA = ∠OCB，
∴∠DCO = ∠ACB = 60°，
∴△COD是等边三角形。
(2)【解】
∵△ADC≌△BOC，
∴∠ADC = ∠BOC = α。
∵△COD是等边三角形，
∴∠COD = ∠CDO = 60°，
∴∠AOD = 360° - ∠AOB - ∠BOC - ∠COD = 360° - 110° - α - 60° = 190° - α，∠ADO = ∠ADC - ∠CDO = α - 60°。
∵AO = AD，
∴∠ADO = ∠AOD，
∴α - 60° = 190° - α，解得α = 125°。

6 [中]在△ABC中,AB= AC,D是BC边的中点,E,F分别是AD,AC边上的点.
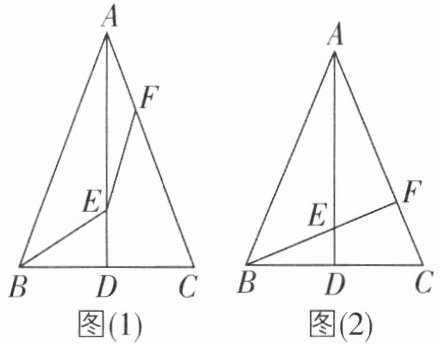
(1)如图(1),连结BE,EF,若∠ABE= ∠EFC,求证：BE= EF；
(2)如图(2),若B,E,F在一条直线上,且∠ABE= ∠BAC= 45°,探究BD与AE之间的数量关系,并说明理由.

答案：

(1)【证明】连结CE，如图
(1)。
∵AB = AC，D是BC边的中点
∴AD⊥BC，∠ABC = ∠ACB。在△BED和△CED中，{DE = DE，∠BDE = ∠CDE，BD = CD，
∴△BED≌△CED(SAS)，
∴BE = CE，
∴∠EBC = ∠ECB，
∴∠ABC - ∠EBC = ∠ACB - ∠ECB，即∠ABE = ∠ACE。
∵∠ABE = ∠EFC，
∴∠ACE = ∠EFC，
∴EF = CE，
∴BE = EF。

(2)【解】AE = 2BD。理由如下：连结CE，如图
(2)。由
(1)得，∠ABE = ∠ACE。
∵∠ABE = ∠BAC = 45°，
∴∠AFB = ∠CFE = 90°，
∴△ABF和△CEF都是等腰直角三角形，
∴AF = BF，CF = EF。在△CBF和△EAF中，{BF = AF，∠BFC = ∠AFE，CF = EF，
∴△CBF≌△EAF(SAS)，
∴BC = AE。
∵BC = 2BD，
∴AE = 2BD。

7 [中]若△ABC和△ADE均为等腰三角形,且AB= AC= AD= AE,当∠ABC和∠ADE互余时,称△ABC与△ADE互为“底余等腰三角形”,△ABC的边BC上的高AH叫做△ADE的“余高”.如图,△ABC与△ADE互为“底余等腰三角形”.
(1)若连结BD,CE,判断△ABD与△ACE是否互为“底余等腰三角形”,并说明理由.
(2)当∠BAC= 90°时,若△ADE的“余高”AH= 3,则DE= ______.
(3)当0°＜∠BAC＜180°时,判断DE与AH之间的数量关系,并说明理由.

答案：

(1)【解】是。理由：如图
(1)，
∵AB = AC = AD = AE，
∴∠ABC = ∠ACB，∠ADE = ∠AED，∠ADB = ∠ABD，∠AEC = ∠ACE，
∴∠ABC + ∠ACB + ∠ADE + ∠AED = 2(∠ABC + ∠ADE)，∠ADB + ∠ABD + ∠AEC + ∠ACE = 2(∠ADB + ∠AEC)。
∵∠ABC + ∠ADE = 90°，
∴2(∠ABC + ∠ADE) = 180°，
∴2(∠ADB + ∠AEC) = 180°，
∴∠ADB + ∠AEC = 90°，
∴△ABD与△ACE互为“底余等腰三角形”。

(2)【解】如图
(2)，
∵∠BAC = 90°，AB = AC = AD = AE，
∴∠B = ∠C = 45°。
∵∠B + ∠D = 90°，
∴∠D = 45°，
∴∠D = ∠E = ∠B = ∠C = 45°在△ADE和△ABC中，{∠E = ∠C，∠D = ∠B，AD = AB，
∴△ADE≌△ABC(AAS)，
∴DE = BC。
∵AB = AC，AH⊥BC，
∴BH = CH，∠HAB = ∠HAC = 45°，
∴AH = BH = CH = 1/2BC = 3，
∴DE = BC = 6，故答案为6。

(3)【解】DE = 2AH。理由：如图
(3)，作AF⊥DE于点F。
∵AD = AE，
∴DF = EF。
∵∠DFA = ∠AHB = 90°，∠B + ∠D = 90°，
∴∠D = ∠BAH = 90° - ∠B。在△DFA和△AHB中，{∠DFA = ∠AHB，∠D = ∠BAH，DA = AB，
∴△DFA≌△AHB，
∴DF = AH，
∴DE = 2DF = 2AH。