第99页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
7. 同一温度的华氏度数y(°F)与摄氏度数x(°C)之间的函数表达式为y= $\frac{9}{5}x+32$.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为
−40
°C.
答案:
−40
8. *某机动车出发前油箱内有油42L,以40km/h的速度匀速行驶一段时间后,到加油站加油,油箱内剩余油量Q(L)与行驶时间t(h)之间的关系如图所示.
(1) 机动车行驶
(2) 根据图象,计算该机动车在行驶过程中每小时的耗油量.
(3) 如果加油站距目的地还有200km,车速仍为40km/h,要到达目的地,油箱内的油是否够用?请说明理由.
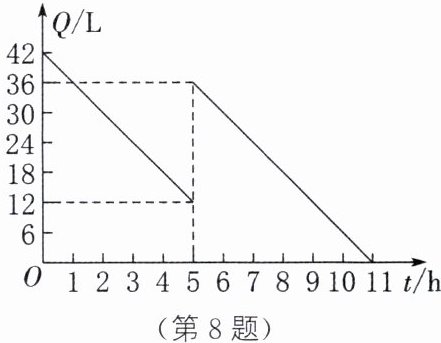
(1) 机动车行驶
5
h后加油,加油24
L.(2) 根据图象,计算该机动车在行驶过程中每小时的耗油量.
(2)(42−12)÷5=6(L),∴该机动车在行驶过程中每小时的耗油量为6L.
(3) 如果加油站距目的地还有200km,车速仍为40km/h,要到达目的地,油箱内的油是否够用?请说明理由.
(3)够用. 理由:∵200÷40=5(h),∴到达目的地还要耗油5×6=30(L).∵机动车途中加油后油箱内剩余油量为36L,36>30,∴够用.

答案:
(1)5;24.
(2)(42−12)÷5=6(L),
∴该机动车在行驶过程中每小时的耗油量为6L.
(3)够用. 理由:
∵200÷40=5(h),
∴到达目的地还要耗油5×6=30(L).
∵机动车途中加油后油箱内剩余油量为36L,36>30,
∴够用.
(1)5;24.
(2)(42−12)÷5=6(L),
∴该机动车在行驶过程中每小时的耗油量为6L.
(3)够用. 理由:
∵200÷40=5(h),
∴到达目的地还要耗油5×6=30(L).
∵机动车途中加油后油箱内剩余油量为36L,36>30,
∴够用.
9. (2024·武汉模拟)一个有进水管与出水管的容器,已知进水速度为每分钟5L,出水速度为每分钟4L,某个时间段内容器内的水量y(L)与时间x(min)之间的关系如图所示,则图中t的值为____
4.5
.
答案:
解:由图可知,0到t分钟容器内水量增加,t到12分钟容器内水量继续增加。
0到t分钟,只有进水管打开,进水速度为5L/min,所以水量y=5x。t分钟时水量为5t。
t到12分钟,进水管和出水管同时打开,净进水速度为5-4=1L/min,此阶段水量从5t增加到30L,时间为(12-t)min。
可得方程:5t + 1×(12 - t) = 30
5t + 12 - t = 30
4t = 18
t = 4.5
答案:4.5
0到t分钟,只有进水管打开,进水速度为5L/min,所以水量y=5x。t分钟时水量为5t。
t到12分钟,进水管和出水管同时打开,净进水速度为5-4=1L/min,此阶段水量从5t增加到30L,时间为(12-t)min。
可得方程:5t + 1×(12 - t) = 30
5t + 12 - t = 30
4t = 18
t = 4.5
答案:4.5
10. 如图①,小钱家、体育公园、文具店依次在同一条马路上.某日,小钱步行从家出发,先到体育公园锻炼20min,再到文具店,用了5min购买文具,然后按原路返回家中.已知小钱往返途中的步行速度不变,设小钱从家出发xmin时,距家ym,y关于x的部分图象如图②所示.
(1) 求小钱的步行速度.
(2) 求小钱从文具店回家过程中y关于x的函数表达式,并补全图象.
(3) 当小钱从家出发tmin时,弟弟小塘以和小钱相同的速度从家中出发,沿相同路线前往文具店.若小钱从文具店返回途中恰好与小塘在体育公园相遇,求t的值.
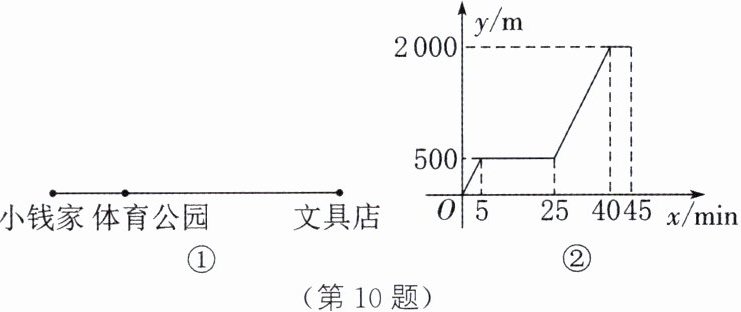
(1) 求小钱的步行速度.
(2) 求小钱从文具店回家过程中y关于x的函数表达式,并补全图象.
(3) 当小钱从家出发tmin时,弟弟小塘以和小钱相同的速度从家中出发,沿相同路线前往文具店.若小钱从文具店返回途中恰好与小塘在体育公园相遇,求t的值.

答案:
(1)2000÷(40−20)=100(m/min),
∴小钱的步行速度为100m/min.
(2)由题意,可得小钱返回耗时20min,即回到家中为第65分钟. 当45≤x≤65时,y=2000−100(x−45)=−100x+6500.补全图象如图所示.
(3)小塘从家中到体育公园所需的时间为500÷100=5(min),
∴t+5=45+(2000−500)÷100,解得t=55.
(1)2000÷(40−20)=100(m/min),
∴小钱的步行速度为100m/min.
(2)由题意,可得小钱返回耗时20min,即回到家中为第65分钟. 当45≤x≤65时,y=2000−100(x−45)=−100x+6500.补全图象如图所示.
(3)小塘从家中到体育公园所需的时间为500÷100=5(min),
∴t+5=45+(2000−500)÷100,解得t=55.
查看更多完整答案,请扫码查看


