《2025年拔尖特训八年级数学上册苏科版》

7. 将数$-\sqrt {5}$、$\sqrt {7}$、$\sqrt {13}$表示在如图所示的数轴上,其中,能被墨迹覆盖的数是√7.

答案： √7

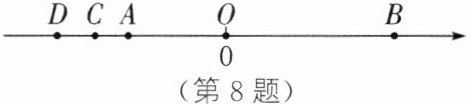
8. 如图,实数$-\sqrt {5}$、$\sqrt {15}$、m在数轴上所对应的点分别为A、B、C,点B关于原点O的对称点为D.若m为整数,则m的值为____.

-3

答案： -3 解析:
∵点B表示的数为√15,点B关于原点O的对称点为D,
∴点D表示的数为-√15.
∵点C在点A、D之间,
∴-√15＜m＜-√5.
∵-4＜-√15＜-3,-3＜-√5＜-2,
∴-√15＜-3＜-√5.
∵m为整数,
∴m的值为-3.

9. 如图,在数轴上竖直摆放一个直径为4个单位长度的半圆,A是半圆弧的中点,半圆直径的一个端点位于原点O.该半圆沿数轴从原点O开始向右无滑动滚动,当点A第一次落在数轴上时,点A表示的数为4+π.

答案： 4+π 解析:由题意,可得当点A第一次落在数轴上时,点A表示的数为4+1/2×1/2×π×4=4+π.

10. 为了生产某雕塑,需要把截面面积为$56cm^{2}$、长为32cm的长方体钢体,铸成两个正方体,其中大正方体的棱长是小正方体的3倍.求这两个正方体的棱长.

答案： 设小正方体的棱长为x cm,则大正方体的棱长为3x cm.由题意,得x³+(3x)³=56×32,即28x³=56×32,
∴x³=64.
∴x=4.
∴3x=12.
∴这两个正方体的棱长分别为4 cm和12 cm.

11. 观察求算术平方根的规律:$\sqrt {0.0001}= 0.01$,$\sqrt {0.01}= 0.1$,$\sqrt {1}= 1$,$\sqrt {100}= 10$,$\sqrt {10000}= 100$,…,并利用这个规律解决下列问题:
(1)已知$\sqrt {20}\approx 4.47$,估算$\sqrt {2000}$的值.
(2)已知$\sqrt {3.68}\approx 1.918$,$\sqrt {a}\approx 191.8$,求a的值.
(3)根据上述探究方法,尝试解决问题:已知$\sqrt [3]{n}\approx 1.26$,$\sqrt [3]{m}\approx 12.6$,用含n的代数式表示m.

答案：
(1)
∵√20≈4.47,
∴√2000≈4.47×10=44.7.
(2)
∵191.8=1.918×100,
∴√a=√3.68×10000=√36800.
∴a=36800.
(3)
∵1.26×10=12.6,
∴√[3](1000n)=√[3](m).
∴1000n=m,即m=1000n.