《2025年拔尖特训八年级数学上册苏科版》

8. 在$△ABC$中,$AB= 15$,$AC= 13$,边BC上的高$AD= 12$,则边BC的长为14或4.

答案： 14或4

9. 如图,某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长$BC= 6m$,$AC= 8m$.现要将其扩建成等腰三角形ABD,且扩建部分是以AC为直角边的直角三角形ACD.求扩建后的等腰三角形ABD的面积.

答案：
如图①，当AB=AD时，易得BD=12m，
∴$S_{\triangle ABD}=\frac{1}{2}×8×12=48(m^{2})$.如图②，当AB=BD时，
∵BC=6m，AC=8m，
∴易得AB=10m.
∴BD=10m.
∴$S_{\triangle ABD}=\frac{1}{2}×8×10=40(m^{2})$.如图③，当AD=BD时，设CD=xm，则AD=BD=(x+6)m.在Rt△ACD中，$AC^{2}+CD^{2}=AD^{2}$，
∴$8^{2}+x^{2}=(x+6)^{2}$，解得x=$\frac{7}{3}$.
∴$S_{\triangle ABD}=\frac{1}{2}×8×(6+\frac{7}{3})=\frac{100}{3}(m^{2})$.综上所述，扩建后的等腰三角形ABD的面积为48$m^{2}$或40$m^{2}$或$\frac{100}{3}m^{2}$.

10. 如图,在$△ABC$中,$∠C= 90^{\circ }$,$AB= 5cm$,$BC= 3cm$,若动点P从点C开始,按$C→A→B$的路径运动,且速度为$1cm/s$.设运动的时间为ts.
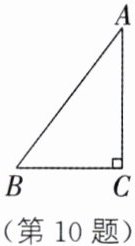
(1) 当点P运动6.5s时,求CP和BP的长.
(2) 当t满足什么条件时,$△BCP$为直角三角形?

答案：

(1)
∵∠C=90°，AB=5cm，BC=3cm，
∴易得AC=4cm.
∵动点P从点C开始以1cm/s的速度运动，
∴运动6.5s后，点P在线段AB上，此时AP=2.5cm，即P是AB的中点.
∴BP=CP=$\frac{1}{2}AB=2.5cm$.
(2)①当点P在AC上运动时，△BCP为直角三角形，
∴0＜t≤4.
②如图，当点P在AB上时，若CP⊥AB，则△BCP为直角三角形.
∵$\frac{1}{2}AB\cdot CP=\frac{1}{2}AC\cdot BC$，
∴CP=$\frac{AC\cdot BC}{AB}=\frac{12}{5}cm$.
∴$AP^{2}=AC^{2}-CP^{2}=\frac{256}{25}cm^{2}$.
∴AP=$\frac{16}{5}cm$.
∴AC+AP=4+$\frac{16}{5}=\frac{36}{5}(cm)$.
∴t=$\frac{36}{5}÷1=\frac{36}{5}$.综上所述，当0＜t≤4或t=$\frac{36}{5}$时，△BCP为直角三角形.

11. 在$Rt△ABC$中,$∠C= 90^{\circ }$,M为边AB的中点,点D在边BC上,连接MD.
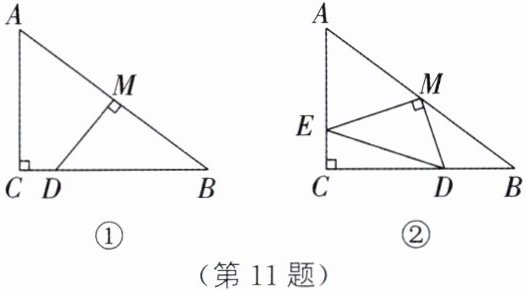
(1) 如图①,若$AC= 3$,$BC= 4$,$MD⊥AB$,求MD的长.
(2) 如图②,过点M作$ME⊥MD$,与边AC交于点E,连接DE,试猜想线段AE、DE、DB三者之间的数量关系,并证明你的结论.

答案：

(1)如图①，连接AD.
∵MD⊥AB，且M为边AB的中点，
∴MD是线段AB的垂直平分线.
∴AD=BD.设AD=x，则BD=x，CD=BC - BD=4-x.在Rt△ACD中，$AD^{2}=AC^{2}+CD^{2}$，即$x^{2}=3^{2}+(4-x)^{2}$，解得x=$\frac{25}{8}$.
∴AD=$\frac{25}{8}$.在Rt△ACB中，$AB^{2}=AC^{2}+BC^{2}=3^{2}+4^{2}=25$，
∴AB=5.
∴AM=$\frac{1}{2}AB=\frac{5}{2}$.
∴$MD^{2}=AD^{2}-AM^{2}=\frac{225}{64}$.
∴MD=$\frac{15}{8}$.
(2)$AE^{2}+DB^{2}=DE^{2}$.如图②，延长EM到点F，使得ME=MF，连接DF、BF.
∵M为AB的中点，
∴MA=MB.在△MAE和△MBF中，$\left\{\begin{array}{l} ME=MF\\ \angle AME=\angle BMF\\ MA=MB\end{array}\right.$，
∴△MAE≌△MBF.
∴AE=BF，∠A=∠MBF.
∵ME⊥MD，
∴易得DF=DE.在Rt△ACB中，
∵∠A+∠ABC=90°，
∴∠FBD=∠MBF+∠ABC=∠A+∠ABC=90°.在Rt△DFB中，
∵$BF^{2}+DB^{2}=DF^{2}$，
∴$AE^{2}+DB^{2}=DE^{2}$.