第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
6. 如图,在$\triangle ABC$中,$AB= AC$,$AD⊥BC$于点D,AM是$\triangle ABC的外角∠CAE$的平分线.
(1)求证:$AM// BC$.
(2)若DN平分$∠ADC$,交AM于点N,试判断$\triangle ADN$的形状,并说明理由.

(1)求证:$AM// BC$.
(2)若DN平分$∠ADC$,交AM于点N,试判断$\triangle ADN$的形状,并说明理由.

答案:
6.
(1)
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC.
∵AM平分∠EAC,
∴∠EAM=∠MAC=$\frac{1}{2}$∠EAC.
∴∠MAD=∠MAC+∠CAD=$\frac{1}{2}$∠EAC+$\frac{1}{2}$∠BAC=$\frac{1}{2}$×180°=90°.
∵AD⊥BC,
∴∠ADC=90°.
∴∠MAD+∠ADC=180°.
∴AM//BC.
(2)△ADN是等腰直角三角形.理由:
∵AM//BC,
∴∠AND=∠NDC.
∵DN平分∠ADC,
∴∠ADN=∠NDC=∠AND.
∴AD=AN.由
(1),得∠MAD=90°,
∴△ADN是等腰直角三角形.
(1)
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC.
∵AM平分∠EAC,
∴∠EAM=∠MAC=$\frac{1}{2}$∠EAC.
∴∠MAD=∠MAC+∠CAD=$\frac{1}{2}$∠EAC+$\frac{1}{2}$∠BAC=$\frac{1}{2}$×180°=90°.
∵AD⊥BC,
∴∠ADC=90°.
∴∠MAD+∠ADC=180°.
∴AM//BC.
(2)△ADN是等腰直角三角形.理由:
∵AM//BC,
∴∠AND=∠NDC.
∵DN平分∠ADC,
∴∠ADN=∠NDC=∠AND.
∴AD=AN.由
(1),得∠MAD=90°,
∴△ADN是等腰直角三角形.
7. 如图,在等腰三角形ABC中,$AB= AC$,D、E分别为AB、AC上的点,且满足$AE= AD$.
(1)求证:$∠ABE= ∠ACD$.
(2)连接AO,试判断AO与BC的位置关系,并予以证明.
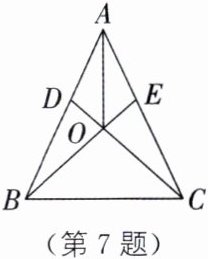
(1)求证:$∠ABE= ∠ACD$.
(2)连接AO,试判断AO与BC的位置关系,并予以证明.

答案:
7.
(1)在△ABE和△ACD中$\left\{\begin{array}{l}AB=AC,\\ ∠BAE=∠CAD,\\ AE=AD,\end{array}\right.$
∴△ABE≌△ACD.
∴∠ABE=∠ACD.
(2)AO⊥BC.
∵AB=AC,
∴∠ABC=∠ACB.
∵∠ABE=∠ACD,
∴∠ABC−∠ABE=∠ACB−∠ACD.
∴∠OBC=∠OCB.
∴OB=OC.又
∵AB=AC,
∴点O、A在线段BC的垂直平分线上,
∴AO⊥BC.
(1)在△ABE和△ACD中$\left\{\begin{array}{l}AB=AC,\\ ∠BAE=∠CAD,\\ AE=AD,\end{array}\right.$
∴△ABE≌△ACD.
∴∠ABE=∠ACD.
(2)AO⊥BC.
∵AB=AC,
∴∠ABC=∠ACB.
∵∠ABE=∠ACD,
∴∠ABC−∠ABE=∠ACB−∠ACD.
∴∠OBC=∠OCB.
∴OB=OC.又
∵AB=AC,
∴点O、A在线段BC的垂直平分线上,
∴AO⊥BC.
8. *在$\triangle ABC$中,$AB= AC$,点E在AB上,以BE为底边,在$\triangle ABC$内作等腰三角形DBE,取CE的中点G,连接AG、DG.
(1)如图①,若$BE= AE$,$∠BDE= 120^{\circ }$,$∠BAC= 60^{\circ }$,求证:$AG⊥DG$.
(2)如图②,若$BE≠AE$,$∠BDE+∠BAC= 180^{\circ }$,则问题(1)中的结论仍然成立吗?请说明理由.

(1)如图①,若$BE= AE$,$∠BDE= 120^{\circ }$,$∠BAC= 60^{\circ }$,求证:$AG⊥DG$.
(2)如图②,若$BE≠AE$,$∠BDE+∠BAC= 180^{\circ }$,则问题(1)中的结论仍然成立吗?请说明理由.

答案:
8.
(1)如图①,延长DG至点H,使GH=GD,连接AD、AH、CH.
∵G为CE的中点,
∴GC=GE.在△CHG和△EDG中,
∵GH=GD,∠CGH=∠EGD,GC=GE,
∴△CHG≌△EDG.
∴CH=ED,∠HCG=∠DEG.
∵△DBE是等腰三角形,∠BDE=120°,
∴ BD=ED=CH,∠BED=∠EBD=30°.
∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形.
∴AC=BC,∠ACB=60°.
∵BE=AE,
∴CE⊥AB,∠ACE=$\frac{1}{2}$∠ACB=30°.
∴∠BED+∠DEG=90°,∠BAC+∠ACE=90°.
∴∠HCG=∠DEG=60°.
∴∠ACH=∠HCG−∠ACE=30°.
∴∠ABD=∠ACH.在△ABD和△ACH中,
∵AB=AC,∠ABD=∠ACH,BD=CH,
∴△ABD≌△ACH.
∴AD=AH.
∵HG=DG,
∴AG⊥DG.
(2)问题
(1)中的结论仍然成立.理由:如图②,延长DG至点M,使GM=GD,连接AD、AM、CM.
∵G为CE的中点,
∴GC=GE.在△CMG和△EDG中,
∵GM=GD,∠CGM=∠EGD,GC=GE,
∴△CMG≌△EDG.
∴CM=ED,∠MCG=∠DEG.
∵△DBE是等腰三角形,
∴ BD=ED=CM,∠BED=∠EBD=$\frac{1}{2}$(180°−∠BDE).
∵∠BDE+∠BAC=180°,
∴∠BAC=180°−∠BDE.
∴∠BAC=2∠BED=2∠EBD.
∵∠BEC=∠BED+∠DEG=∠BAC+∠ACE,
∴∠BED+∠MCG=∠BAC+∠ACE.
∵∠MCG=∠ACM+∠ACE,
∴∠BED+∠ACM+∠ACE=2∠BED+∠ACE.
∴∠ACM=∠BED=∠ABD.在△ABD和△ACM中,
∵AB=AC,∠ABD=∠ACM,BD=CM,
∴△ABD≌△ACM.
∴AD=AM.
∵MG=DG,
∴AG⊥DG.

8.
(1)如图①,延长DG至点H,使GH=GD,连接AD、AH、CH.
∵G为CE的中点,
∴GC=GE.在△CHG和△EDG中,
∵GH=GD,∠CGH=∠EGD,GC=GE,
∴△CHG≌△EDG.
∴CH=ED,∠HCG=∠DEG.
∵△DBE是等腰三角形,∠BDE=120°,
∴ BD=ED=CH,∠BED=∠EBD=30°.
∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形.
∴AC=BC,∠ACB=60°.
∵BE=AE,
∴CE⊥AB,∠ACE=$\frac{1}{2}$∠ACB=30°.
∴∠BED+∠DEG=90°,∠BAC+∠ACE=90°.
∴∠HCG=∠DEG=60°.
∴∠ACH=∠HCG−∠ACE=30°.
∴∠ABD=∠ACH.在△ABD和△ACH中,
∵AB=AC,∠ABD=∠ACH,BD=CH,
∴△ABD≌△ACH.
∴AD=AH.
∵HG=DG,
∴AG⊥DG.
(2)问题
(1)中的结论仍然成立.理由:如图②,延长DG至点M,使GM=GD,连接AD、AM、CM.
∵G为CE的中点,
∴GC=GE.在△CMG和△EDG中,
∵GM=GD,∠CGM=∠EGD,GC=GE,
∴△CMG≌△EDG.
∴CM=ED,∠MCG=∠DEG.
∵△DBE是等腰三角形,
∴ BD=ED=CM,∠BED=∠EBD=$\frac{1}{2}$(180°−∠BDE).
∵∠BDE+∠BAC=180°,
∴∠BAC=180°−∠BDE.
∴∠BAC=2∠BED=2∠EBD.
∵∠BEC=∠BED+∠DEG=∠BAC+∠ACE,
∴∠BED+∠MCG=∠BAC+∠ACE.
∵∠MCG=∠ACM+∠ACE,
∴∠BED+∠ACM+∠ACE=2∠BED+∠ACE.
∴∠ACM=∠BED=∠ABD.在△ABD和△ACM中,
∵AB=AC,∠ABD=∠ACM,BD=CM,
∴△ABD≌△ACM.
∴AD=AM.
∵MG=DG,
∴AG⊥DG.

查看更多完整答案,请扫码查看


