第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 如图,原来从A村到B村,需要沿路线A→C→B($∠C= 90^{\circ }$)行走,以绕过两村间的一片湖. 在湖上建好桥后,可直接从A村到B村. 若$AC= 5km$,$BC= 12km$,则建好桥后从A村到B村比原来减少的路程为 (
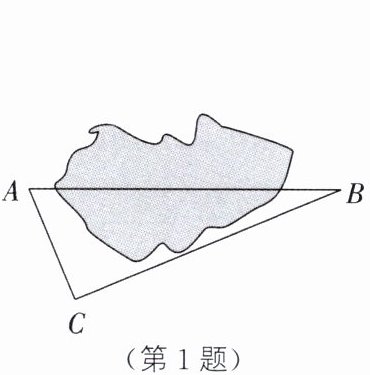
A.2 km
B.4 km
C.10 km
D.14 km
]
B
)
A.2 km
B.4 km
C.10 km
D.14 km
]
答案:
B
2. 如图,小明以广场为出发点,先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米,小明到达的终点与原出发点之间的距离为 (
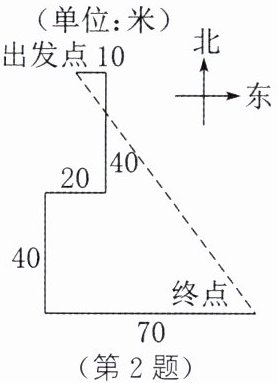
A.80米
B.100米
C.110米
D.180米
]
B
)
A.80米
B.100米
C.110米
D.180米
]
答案:
B
3. 小明想测量旗杆的高度,如图,他先将升旗的绳子拉到旗杆底端,并在绳子对应旗杆底端的位置上打了一个结,然后将绳子拉到离旗杆底部4m处,绳头恰好接触到地面,发现此时绳头距打结处为1m. 旗杆的高度为
7.5
m.
答案:
7.5
4. 如图,校园内有一块长方形草坪ABCD,$AB= 8m$,$BC= 6m$,从点A到点C,同学们为了抄近路,常沿线段AC走. 同学们少走了
4
m.
答案:
4
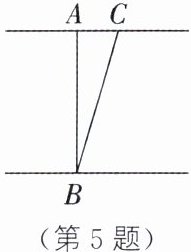
5. 如图,某渡船从点B处沿着与河岸垂直的路线AB横渡,由于受水流的影响,实际沿着BC航行,上岸地点C与欲到达地点A相距70m,结果发现BC比河宽AB多10m,求该河的宽度AB(两岸可近似看成平行).
]
]

答案:
设AB=x m,则BC=(x+10)m.在Rt△ABC中,根据勾股定理,得x²+70²=(x+10)²,解得x=240.
∴该河的宽度AB为240 m.
∴该河的宽度AB为240 m.
6. 如图,某自动感应门的正上方A处装有一个感应器,其离地面的高度AB为2.5米,一名学生站在C处时,感应门自动打开了,此时这名学生离感应门的距离BC为1.2米,头顶离感应器的距离AD为1.5米,则这名学生的身高CD为 (
A.0.9米
B.1.3米
C.1.5米
D.1.6米
]
D
)A.0.9米
B.1.3米
C.1.5米
D.1.6米
]
答案:
D
7. 如图,钓竿AC的长为10m,露在水面上的渔线BC的长为6m,某钓鱼者想看看鱼钩上的情况,把竿AC转动到AC'的位置,此时露在水面上的渔线B'C'的长为8m,则点B、B'之间的距离为 (
A.1m
B.2m
C.3m
D.4m
]
B
)A.1m
B.2m
C.3m
D.4m
]
答案:
B 解析:易得点B'在线段AB上.在Rt△ABC中,
∵AB²+BC²=AC²,AC=10 m,BC=6 m,
∴AB=8 m.在Rt△AB'C'中,
∵AB'²+B'C'²=AC'²,AC'=10 m,B'C'=8 m,
∴AB'=6 m.
∴BB'=AB - AB'=8 - 6=2(m).
∵AB²+BC²=AC²,AC=10 m,BC=6 m,
∴AB=8 m.在Rt△AB'C'中,
∵AB'²+B'C'²=AC'²,AC'=10 m,B'C'=8 m,
∴AB'=6 m.
∴BB'=AB - AB'=8 - 6=2(m).
查看更多完整答案,请扫码查看


