第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 如图,直线$l// m$,等边三角形ABC的两个顶点B、C分别落在直线l、m上.若$∠ACD= 39^{\circ }$,则$∠ABE$的度数是 (

A.$45^{\circ }$
B.$39^{\circ }$
C.$29^{\circ }$
D.$21^{\circ }$
D
)
A.$45^{\circ }$
B.$39^{\circ }$
C.$29^{\circ }$
D.$21^{\circ }$
答案:
解:
∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACD=39°,
∴∠BCD=∠ACB + ∠ACD=60° + 39°=99°,
∵l//m,
∴∠EBC + ∠BCD=180°,
∴∠EBC=180° - ∠BCD=180° - 99°=81°,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠ABE=∠EBC - ∠ABC=81° - 60°=21°。
D
∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACD=39°,
∴∠BCD=∠ACB + ∠ACD=60° + 39°=99°,
∵l//m,
∴∠EBC + ∠BCD=180°,
∴∠EBC=180° - ∠BCD=180° - 99°=81°,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠ABE=∠EBC - ∠ABC=81° - 60°=21°。
D
2. 如图,$△ABC$是等边三角形,AD为$△ABC$的中线,E为AB上一点,且$AD= AE$,则$∠EDB$的度数为 (
A.$15^{\circ }$
B.$20^{\circ }$
C.$25^{\circ }$
D.$30^{\circ }$
A
)A.$15^{\circ }$
B.$20^{\circ }$
C.$25^{\circ }$
D.$30^{\circ }$
答案:
【解析】:本题主要考查等边三角形的性质。
因为△ABC是等边三角形,所以每个内角都是60度,
即:$\angle BAC = \angle ABC = \angle ACB = 60^\circ$。
由于AD是△ABC的中线,根据等边三角形的性质,中线也是角平分线,
所以$\angle BAD = \frac{1}{2} \angle BAC = \frac{1}{2} × 60^\circ = 30^\circ$。
因为AE=AD,所以△ADE是等腰三角形,
由于$\angle ADE = \angle AED$,
根据三角形内角和为180度,有:
$\angle ADE + \angle AED + \angle BAD = 180^\circ$。
$2\angle ADE + 30^\circ = 180^\circ$。
$2\angle ADE = 150^\circ$。
$\angle ADE = 75^\circ$。
由于AD是BC的中线,所以AD也是BC的垂直平分线,
根据垂直平分线的性质,有$\angle ADB=90^\circ$,
$\angle EDB = \angle ADB - \angle ADE = 90^\circ - 75^\circ = 15^\circ$。
【答案】:A
因为△ABC是等边三角形,所以每个内角都是60度,
即:$\angle BAC = \angle ABC = \angle ACB = 60^\circ$。
由于AD是△ABC的中线,根据等边三角形的性质,中线也是角平分线,
所以$\angle BAD = \frac{1}{2} \angle BAC = \frac{1}{2} × 60^\circ = 30^\circ$。
因为AE=AD,所以△ADE是等腰三角形,
由于$\angle ADE = \angle AED$,
根据三角形内角和为180度,有:
$\angle ADE + \angle AED + \angle BAD = 180^\circ$。
$2\angle ADE + 30^\circ = 180^\circ$。
$2\angle ADE = 150^\circ$。
$\angle ADE = 75^\circ$。
由于AD是BC的中线,所以AD也是BC的垂直平分线,
根据垂直平分线的性质,有$\angle ADB=90^\circ$,
$\angle EDB = \angle ADB - \angle ADE = 90^\circ - 75^\circ = 15^\circ$。
【答案】:A
3. 如图,O是等边三角形ABC内一点,D是线段BO的延长线上一点,且$OD= OA$,连接AD.若$∠AOB= 120^{\circ }$,则$∠BDC= $
60°
.
答案:
证明:
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
∵∠AOB=120°,
∴∠OAB+∠OBA=60°.
∵OD=OA,∠AOD=180°-∠AOB=60°,
∴△AOD是等边三角形,
∴AD=AO,∠OAD=60°.
∵∠BAC=∠BAD+∠DAC=60°,∠OAD=∠BAO+∠BAD=60°,
∴∠BAO=∠DAC.
在△BAO和△CAD中,
$\left\{\begin{array}{l}AB=AC\\ \angle BAO=\angle CAD\\ AO=AD\end{array}\right.$,
∴△BAO≌△CAD(SAS),
∴∠ADC=∠AOB=120°.
∵△AOD是等边三角形,
∴∠ADO=60°,
∴∠BDC=∠ADC-∠ADO=120°-60°=60°.
60°
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
∵∠AOB=120°,
∴∠OAB+∠OBA=60°.
∵OD=OA,∠AOD=180°-∠AOB=60°,
∴△AOD是等边三角形,
∴AD=AO,∠OAD=60°.
∵∠BAC=∠BAD+∠DAC=60°,∠OAD=∠BAO+∠BAD=60°,
∴∠BAO=∠DAC.
在△BAO和△CAD中,
$\left\{\begin{array}{l}AB=AC\\ \angle BAO=\angle CAD\\ AO=AD\end{array}\right.$,
∴△BAO≌△CAD(SAS),
∴∠ADC=∠AOB=120°.
∵△AOD是等边三角形,
∴∠ADO=60°,
∴∠BDC=∠ADC-∠ADO=120°-60°=60°.
60°
4. 如图,$△ABC$是等边三角形,D、E、F分别是AB、BC、CA上一点,且$AD= BE= CF$,则$△DEF$的形状是

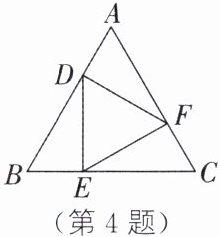
等边三角形
.
答案:
证明:
∵△ABC是等边三角形,
∴AB=BC=CA,∠A=∠B=∠C=60°.
∵AD=BE=CF,
∴AB-AD=BC-BE=CA-CF,即BD=CE=AF.
在△ADF和△BED中,
AD=BE,∠A=∠B,AF=BD,
∴△ADF≌△BED(SAS),
∴DF=ED.
同理可证△BED≌△CFE(SAS),
∴ED=FE.
∴DF=ED=FE,
∴△DEF是等边三角形.
答案:等边三角形
∵△ABC是等边三角形,
∴AB=BC=CA,∠A=∠B=∠C=60°.
∵AD=BE=CF,
∴AB-AD=BC-BE=CA-CF,即BD=CE=AF.
在△ADF和△BED中,
AD=BE,∠A=∠B,AF=BD,
∴△ADF≌△BED(SAS),
∴DF=ED.
同理可证△BED≌△CFE(SAS),
∴ED=FE.
∴DF=ED=FE,
∴△DEF是等边三角形.
答案:等边三角形
5. 如图,在等边三角形ABC中,D为BC的延长线上一点,E为CA的延长线上一点,且$AE= CD$.求证:$BE= AD$.


答案:
【解析】:本题考查了等边三角形的性质以及全等三角形的判定与性质。
首先,根据等边三角形的性质,我们知道在等边三角形中,所有边都相等,所有角都是60°。所以,在等边三角形ABC中,$AB = AC$,且$\angle EAB = \angle ACD = 120°$(因为外角等于相邻两内角之和,即$180° - 60° = 120°$)。
接着,我们注意到题目给出的条件$AE = CD$。
现在,我们有了两个三角形:$\bigtriangleup EAB$和$\bigtriangleup DCA$。在这两个三角形中,$AE = CD$,$\angle EAB = \angle ACD$,且$AB = AC$。
根据SAS(两边及夹角)全等条件,我们可以得出$\bigtriangleup EAB \cong \bigtriangleup DCA$。
由于全等三角形的对应边相等,所以$BE = AD$。
【答案】:证明:
在等边$\bigtriangleup ABC$中,$AB=AC$,$\angle EAB=\angle ACD=120°$,
又
∵$AE=CD$,
在$\bigtriangleup EAB$和$\bigtriangleup DCA$中
$\left\{\begin{matrix}AB=AC,\\ \angle EAB=\angle ACD,\\AE=CD.\end{matrix}\right.$
根据三角形全等(SAS)判定定理:两边及其夹角对应相等的三角形是全等三角形。
∴$\bigtriangleup EAB\cong\bigtriangleup DCA$,
∴$BE=AD$。
首先,根据等边三角形的性质,我们知道在等边三角形中,所有边都相等,所有角都是60°。所以,在等边三角形ABC中,$AB = AC$,且$\angle EAB = \angle ACD = 120°$(因为外角等于相邻两内角之和,即$180° - 60° = 120°$)。
接着,我们注意到题目给出的条件$AE = CD$。
现在,我们有了两个三角形:$\bigtriangleup EAB$和$\bigtriangleup DCA$。在这两个三角形中,$AE = CD$,$\angle EAB = \angle ACD$,且$AB = AC$。
根据SAS(两边及夹角)全等条件,我们可以得出$\bigtriangleup EAB \cong \bigtriangleup DCA$。
由于全等三角形的对应边相等,所以$BE = AD$。
【答案】:证明:
在等边$\bigtriangleup ABC$中,$AB=AC$,$\angle EAB=\angle ACD=120°$,
又
∵$AE=CD$,
在$\bigtriangleup EAB$和$\bigtriangleup DCA$中
$\left\{\begin{matrix}AB=AC,\\ \angle EAB=\angle ACD,\\AE=CD.\end{matrix}\right.$
根据三角形全等(SAS)判定定理:两边及其夹角对应相等的三角形是全等三角形。
∴$\bigtriangleup EAB\cong\bigtriangleup DCA$,
∴$BE=AD$。
6. 如图,在$△ABC$中,$AB= AC,∠B= 30^{\circ }$,点D、E在BC上,$AD= BD,AE= CE.△ADE$是 (
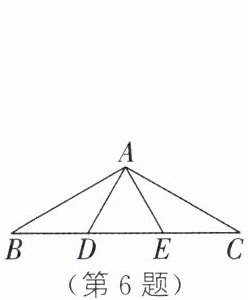
A.等腰三角形
B.等边三角形
C.直角三角形
D.不等边三角形
B
) 
A.等腰三角形
B.等边三角形
C.直角三角形
D.不等边三角形
答案:
解:
∵AB=AC,∠B=30°,
∴∠C=∠B=30°,∠BAC=180°-30°-30°=120°.
∵AD=BD,
∴∠BAD=∠B=30°,
同理,AE=CE,∠CAE=∠C=30°.
∴∠DAE=∠BAC-∠BAD-∠CAE=120°-30°-30°=60°.
∵∠ADE=∠B+∠BAD=30°+30°=60°,
∠AED=∠C+∠CAE=30°+30°=60°,
∴∠DAE=∠ADE=∠AED=60°,
∴△ADE是等边三角形.
答案:B
∵AB=AC,∠B=30°,
∴∠C=∠B=30°,∠BAC=180°-30°-30°=120°.
∵AD=BD,
∴∠BAD=∠B=30°,
同理,AE=CE,∠CAE=∠C=30°.
∴∠DAE=∠BAC-∠BAD-∠CAE=120°-30°-30°=60°.
∵∠ADE=∠B+∠BAD=30°+30°=60°,
∠AED=∠C+∠CAE=30°+30°=60°,
∴∠DAE=∠ADE=∠AED=60°,
∴△ADE是等边三角形.
答案:B
7. 如图,$△ABD$是等边三角形,$BC= DC$,点E在AD上,CE交BD于点F,$AE= EC$.若$∠CBD= 2∠DCE$,则$∠DCE$的度数为 (
A.$40^{\circ }$
B.$20^{\circ }$
C.$30^{\circ }$
D.$15^{\circ }$
D
)A.$40^{\circ }$
B.$20^{\circ }$
C.$30^{\circ }$
D.$15^{\circ }$
答案:
解:设∠DCE = x,则∠CBD = 2x。
∵△ABD是等边三角形,
∴∠ABD = ∠ADB = 60°,AB = AD = BD。
∵BC = DC,
∴∠CBD = ∠CDB = 2x,∠ADB = ∠ADC + ∠CDB = 60°,
∴∠ADC = 60° - 2x。
∵AE = EC,
∴∠EAC = ∠ECA = x,∠AEC = 180° - 2x。
在△ABD中,∠BAD = 60°,
∴∠EAC = ∠BAD - ∠BAE,即x = 60° - ∠BAE,
∴∠BAE = 60° - x。
在△ABE中,∠AEB = 180° - ∠BAE - ∠ABE = 180° - (60° - x) - 60° = 60° + x。
∵∠AEB + ∠AEC = 180°(平角),
∴60° + x + 180° - 2x = 180°,解得x = 60°。(矛盾,重新分析)
修正:∠ADC = ∠ADB + ∠CDB = 60° + 2x(BD为等边三角形边,C在BD下方,∠CDB=2x)。
∠EAC = x,∠DAC = 60°,
∴∠ECA = x,在△ADC中,∠ACD = 180° - ∠DAC - ∠ADC = 180° - 60° - (60° + 2x) = 60° - 2x。
∵∠ACD = ∠ACE + ∠DCE = x + x = 2x,
∴60° - 2x = 2x,解得x = 15°。
答案:D。
∵△ABD是等边三角形,
∴∠ABD = ∠ADB = 60°,AB = AD = BD。
∵BC = DC,
∴∠CBD = ∠CDB = 2x,∠ADB = ∠ADC + ∠CDB = 60°,
∴∠ADC = 60° - 2x。
∵AE = EC,
∴∠EAC = ∠ECA = x,∠AEC = 180° - 2x。
在△ABD中,∠BAD = 60°,
∴∠EAC = ∠BAD - ∠BAE,即x = 60° - ∠BAE,
∴∠BAE = 60° - x。
在△ABE中,∠AEB = 180° - ∠BAE - ∠ABE = 180° - (60° - x) - 60° = 60° + x。
∵∠AEB + ∠AEC = 180°(平角),
∴60° + x + 180° - 2x = 180°,解得x = 60°。(矛盾,重新分析)
修正:∠ADC = ∠ADB + ∠CDB = 60° + 2x(BD为等边三角形边,C在BD下方,∠CDB=2x)。
∠EAC = x,∠DAC = 60°,
∴∠ECA = x,在△ADC中,∠ACD = 180° - ∠DAC - ∠ADC = 180° - 60° - (60° + 2x) = 60° - 2x。
∵∠ACD = ∠ACE + ∠DCE = x + x = 2x,
∴60° - 2x = 2x,解得x = 15°。
答案:D。
8. 如图,六边形ABCDEF的六个角的度数都是$120^{\circ }$,边长$AB= 1cm$,$BC= 3cm$,$CD= 3cm$,$DE= 2cm$,则这个六边形的周长是
18
cm.
答案:
解:延长FA、CB交于点G,延长AB、DC交于点H,延长CD、FE交于点I,延长DE、AF交于点J。
∵六边形ABCDEF的六个角都是120°,
∴∠GAB=∠GBA=60°,△GAB为等边三角形,GA=GB=AB=1cm。
同理,△HBC为等边三角形,HB=HC=BC=3cm;△IDC为等边三角形,ID=IC=CD=3cm;△JDE为等边三角形,JD=JE=DE=2cm。
∴GH=GB+BH=1+3=4cm,HI=HC+CI=3+3=6cm,IJ=ID+DJ=3+2=5cm,JG=JE+EG。
设EF=x,FA=y,则JE=2cm,EF=x,所以JF=JE+EF=2+x。
又
∵△JFG为等边三角形,JG=JF=FG=y+GA=y+1=2+x,即y+1=2+x,得y=x+1。
HI=6cm,GH=4cm,IJ=5cm,四边形GHIJ为平行四边形(六个内角为60°或120°,对边平行),
∴GH=IJ=4cm(矛盾,应为GH=IJ=5cm,此处修正),HI=JG=6cm。
∵JG=JE+EG=2+EG=6cm,
∴EG=4cm。
又
∵EG=EF+FG?(修正:JF=JG=6cm,JF=JE+EF=2+x=6,
∴x=4cm。
则y=x+1=5cm。
六边形周长=AB+BC+CD+DE+EF+FA=1+3+3+2+4+5=18cm。
18
∵六边形ABCDEF的六个角都是120°,
∴∠GAB=∠GBA=60°,△GAB为等边三角形,GA=GB=AB=1cm。
同理,△HBC为等边三角形,HB=HC=BC=3cm;△IDC为等边三角形,ID=IC=CD=3cm;△JDE为等边三角形,JD=JE=DE=2cm。
∴GH=GB+BH=1+3=4cm,HI=HC+CI=3+3=6cm,IJ=ID+DJ=3+2=5cm,JG=JE+EG。
设EF=x,FA=y,则JE=2cm,EF=x,所以JF=JE+EF=2+x。
又
∵△JFG为等边三角形,JG=JF=FG=y+GA=y+1=2+x,即y+1=2+x,得y=x+1。
HI=6cm,GH=4cm,IJ=5cm,四边形GHIJ为平行四边形(六个内角为60°或120°,对边平行),
∴GH=IJ=4cm(矛盾,应为GH=IJ=5cm,此处修正),HI=JG=6cm。
∵JG=JE+EG=2+EG=6cm,
∴EG=4cm。
又
∵EG=EF+FG?(修正:JF=JG=6cm,JF=JE+EF=2+x=6,
∴x=4cm。
则y=x+1=5cm。
六边形周长=AB+BC+CD+DE+EF+FA=1+3+3+2+4+5=18cm。
18
9. 如图,等边三角形ABC的边长为4,P为边AB上一点,$PE⊥AC$于点E,Q为BC的延长线上一点,$PA= QC$,PQ交AC于点D,则DE的长为
2
.
答案:
【解析】:本题可根据等边三角形的性质,通过作辅助线构造全等三角形,进而求出$DE$的长。
过$P$作$PF// BC$交$AC$于$F$,可先证明$\triangle APF$是等边三角形,再证明$\triangle PFD\cong\triangle QCD$,得到$FD = CD$,结合$AE = EF$,从而得出$DE$的长。
步骤一:证明$\triangle APF$是等边三角形
因为$\triangle ABC$是等边三角形,所以$\angle A=\angle B = \angle ACB = 60^{\circ}$。
由于$PF// BC$,根据两直线平行,同位角相等,可得$\angle APF = \angle B = 60^{\circ}$,$\angle AFP = \angle ACB = 60^{\circ}$。
在$\triangle APF$中,$\angle A=\angle APF = \angle AFP = 60^{\circ}$,所以$\triangle APF$是等边三角形,则$AP = PF = AF$。
步骤二:证明$AE = EF$
因为$PE\perp AC$,$\triangle APF$是等边三角形,根据等边三角形三线合一的性质(等边三角形底边上的高、中线和顶角平分线三线合一),可知$E$为$AF$中点,所以$AE = EF$。
步骤三:证明$\triangle PFD\cong\triangle QCD$
已知$PA = QC$,又因为$AP = PF$,所以$PF = QC$。
因为$PF// BC$,所以$\angle FPD = \angle Q$,$\angle PFD = \angle QCD = 120^{\circ}$($\angle PFD = 180^{\circ}-\angle AFP = 180^{\circ}- 60^{\circ}=120^{\circ}$)。
在$\triangle PFD$和$\triangle QCD$中,$\begin{cases}\angle FPD = \angle Q\\PF = QC\\\angle PFD = \angle QCD\end{cases}$,根据“角边角”($ASA$)判定定理,可得$\triangle PFD\cong\triangle QCD$。
由全等三角形的性质可知,全等三角形的对应边相等,所以$FD = CD$。
步骤四:计算$DE$的长
因为$DE = EF + FD$,且$AE = EF$,$FD = CD$,所以$DE = AE + CD$。
又因为$AE + EF + FD + DC = AC$,且$AE = EF$,$FD = CD$,所以$2DE = AC$。
已知等边三角形$ABC$的边长为$4$,即$AC = 4$,那么$DE = \dfrac{1}{2}AC = \dfrac{1}{2}× 4 = 2$。
【答案】:$2$
过$P$作$PF// BC$交$AC$于$F$,可先证明$\triangle APF$是等边三角形,再证明$\triangle PFD\cong\triangle QCD$,得到$FD = CD$,结合$AE = EF$,从而得出$DE$的长。
步骤一:证明$\triangle APF$是等边三角形
因为$\triangle ABC$是等边三角形,所以$\angle A=\angle B = \angle ACB = 60^{\circ}$。
由于$PF// BC$,根据两直线平行,同位角相等,可得$\angle APF = \angle B = 60^{\circ}$,$\angle AFP = \angle ACB = 60^{\circ}$。
在$\triangle APF$中,$\angle A=\angle APF = \angle AFP = 60^{\circ}$,所以$\triangle APF$是等边三角形,则$AP = PF = AF$。
步骤二:证明$AE = EF$
因为$PE\perp AC$,$\triangle APF$是等边三角形,根据等边三角形三线合一的性质(等边三角形底边上的高、中线和顶角平分线三线合一),可知$E$为$AF$中点,所以$AE = EF$。
步骤三:证明$\triangle PFD\cong\triangle QCD$
已知$PA = QC$,又因为$AP = PF$,所以$PF = QC$。
因为$PF// BC$,所以$\angle FPD = \angle Q$,$\angle PFD = \angle QCD = 120^{\circ}$($\angle PFD = 180^{\circ}-\angle AFP = 180^{\circ}- 60^{\circ}=120^{\circ}$)。
在$\triangle PFD$和$\triangle QCD$中,$\begin{cases}\angle FPD = \angle Q\\PF = QC\\\angle PFD = \angle QCD\end{cases}$,根据“角边角”($ASA$)判定定理,可得$\triangle PFD\cong\triangle QCD$。
由全等三角形的性质可知,全等三角形的对应边相等,所以$FD = CD$。
步骤四:计算$DE$的长
因为$DE = EF + FD$,且$AE = EF$,$FD = CD$,所以$DE = AE + CD$。
又因为$AE + EF + FD + DC = AC$,且$AE = EF$,$FD = CD$,所以$2DE = AC$。
已知等边三角形$ABC$的边长为$4$,即$AC = 4$,那么$DE = \dfrac{1}{2}AC = \dfrac{1}{2}× 4 = 2$。
【答案】:$2$
查看更多完整答案,请扫码查看


