第97页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
8. 如图所示为某加油站地下圆柱形储油罐示意图,已知储油罐的长度为d,截面的半径为r(d、r为常量),油面的高度为h,油面的宽度为w,油量为v(h、w、v为变量).有下列四个结论:① w是v的函数;② v是w的函数;③ h是w的函数;④ w是h的函数.其中,正确的是____
①④
.
答案:
①④
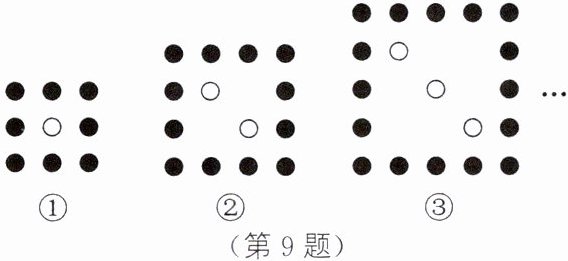
9. 下图中的棋局都是由同样大小的黑棋、白棋按一定规律组成的,其中图①中白棋有1枚,黑棋有8枚;图②中白棋有2枚,黑棋有12枚;图③中白棋有3枚,黑棋有16枚,…,按此规律排列下去,若某个图中白棋有x枚,黑棋有y枚,则y与x之间的关系可以表示为____.
]
]

$y=4x+4$
答案:
$y=4x+4$
10. 有一根弹簧原长10cm,挂重物后(质量不超过50g),它的长度会改变,请根据表格中的数据,解答下列问题:
|质量/g|1|2|3|4|…|
|伸长量/cm|0.5|1|1.5|2|…|
|总长度/cm|10.5|11|11.5|12|…|
(1)要想使弹簧伸长5cm,应挂重物多少克?
(2)当所挂重物的质量为$x g$时,用$h(cm)$表示总长度,此时h与x之间的关系为____.
(3)当弹簧的总长度为25cm时,求此时所挂重物的质量.
|质量/g|1|2|3|4|…|
|伸长量/cm|0.5|1|1.5|2|…|
|总长度/cm|10.5|11|11.5|12|…|
(1)要想使弹簧伸长5cm,应挂重物多少克?
10g
(2)当所挂重物的质量为$x g$时,用$h(cm)$表示总长度,此时h与x之间的关系为____.
h=10+0.5x(0≤x≤50)
(3)当弹簧的总长度为25cm时,求此时所挂重物的质量.
当h=25时,25=10+0.5x,解得x=30.∴当弹簧的总长度为25 cm时,此时所挂重物的质量为30 g.
答案:
(1)$5÷0.5×1=10(g)$,
∴要想使弹簧伸长5 cm,应挂重物10 g.(2)$h=10+0.5x(0≤x≤50)$.(3)当$h=25$时,$25=10+0.5x$,解得$x=30$.
∴当弹簧的总长度为25 cm时,此时所挂重物的质量为30 g.
∴要想使弹簧伸长5 cm,应挂重物10 g.(2)$h=10+0.5x(0≤x≤50)$.(3)当$h=25$时,$25=10+0.5x$,解得$x=30$.
∴当弹簧的总长度为25 cm时,此时所挂重物的质量为30 g.
11. 如图,下列三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系为(
A.$y= 2n+1$
B.$y= 2^{n}+n$
C.$y= 2^{n+1}+n$
D.$y= 2^{n}+n+1$
B
)A.$y= 2n+1$
B.$y= 2^{n}+n$
C.$y= 2^{n+1}+n$
D.$y= 2^{n}+n+1$
答案:
B
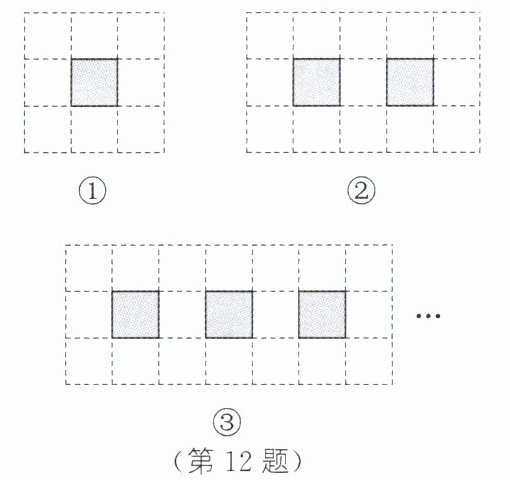
12. 如图①②③,观察下列由白色正方形和灰色正方形组成的图案,并解决下列问题.
(1)图④中有
(2)若在图ⓝ中,白色正方形比灰色正方形多2023个,求n的值.
由(1),得在题图ⓝ中白色正方形有$(5n+3)$个,灰色正方形有n个,$\therefore (5n+3)-n=2023$,解得$n=505$.
∴n的值为505.

(1)图④中有
23
个白色正方形;若图ⓝ中有m个白色正方形,则m与n之间的函数关系为m=5n+3
.(2)若在图ⓝ中,白色正方形比灰色正方形多2023个,求n的值.
由(1),得在题图ⓝ中白色正方形有$(5n+3)$个,灰色正方形有n个,$\therefore (5n+3)-n=2023$,解得$n=505$.
∴n的值为505.
答案:
(1)23;$m=5n+3$. 解析:由题意,知题图①中白色正方形的个数为$8=3+5×1$;题图②中白色正方形的个数为$13=3+5×2$;题图③中白色正方形的个数为$18=3+5×3$……
∴题图④中白色正方形的个数为$3+5×4=23$.
∴题图ⓝ中有$(3+5n)$个白色正方形,即m与n之间的函数关系为$m=5n+3$.(2)由(1),得在题图ⓝ中白色正方形有$(5n+3)$个,灰色正方形有n个,$\therefore (5n+3)-n=2023$,解得$n=505$.
∴n的值为505.
∴题图④中白色正方形的个数为$3+5×4=23$.
∴题图ⓝ中有$(3+5n)$个白色正方形,即m与n之间的函数关系为$m=5n+3$.(2)由(1),得在题图ⓝ中白色正方形有$(5n+3)$个,灰色正方形有n个,$\therefore (5n+3)-n=2023$,解得$n=505$.
∴n的值为505.
查看更多完整答案,请扫码查看


