《2025年拔尖特训八年级数学上册苏科版》

1. 如图,若$\triangle ABC\cong\triangle DFE$,$AC = 6$,$GE = 4$,则$DG$的长为(A)
A.2
B.3
C.4
D.5

答案： A

2. 如图,$\triangle ABC\cong\triangle ADE$,点$D在BC$上,下列结论中,不一定成立的是(D)
A.$\angle BAD= \angle CDE$
B.$BC = DE$
C.$AB = AD$
D.$AB = BD$

答案： D

3. 如图,$\triangle ABC\cong\triangle DEF$,点$C$、$D$、$B$、$F$在同一条直线上,$AC = 3$,$EF = 5$,$CF = 7$,则$BD$的长为1.

答案： 1

4. 如图,$AC$、$BD相交于点O$,$\triangle AOB\cong\triangle COD$,则$AB与CD$的位置关系是AB//CD.

答案： AB//CD

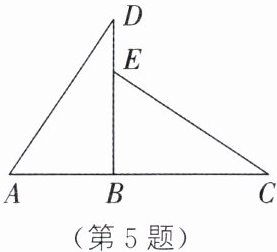
5. 如图,点$A$、$B$、$C$在同一条直线上,点$E在BD$上,且$\triangle ABD\cong\triangle EBC$,$AB = 2\mathrm{cm}$,$BC = 3\mathrm{cm}$.
(1)求$DE$的长.
(2)试判断$AC与BD$的位置关系,并说明理由.

答案：
(1)
∵ △ABD≌△EBC，
∴ BD=BC=3cm,AB=EB=2cm.
∴ DE=BD - EB=1cm.
(2) AC⊥BD.
理由:
∵ △ABD≌△EBC，
∴ ∠ABD=∠EBC.
又
∵ 点A、B、C在同一条直线上，
∴ ∠ABD+∠EBC=180°.
∴ ∠ABD=∠EBC=90°.
∴ AC⊥BD.

6. 将三个全等三角形按如图所示的方式摆放,则$\angle 1+\angle 2+\angle 3$的度数是(D)
A.$90^{\circ}$
B.$120^{\circ}$
C.$135^{\circ}$
D.$180^{\circ}$

答案： D

7. 如图,$N$、$C$、$A$三点在同一条直线上,在$\triangle ABC$中,$\angle A:\angle ABC:\angle ACB = 3:5:10$. 若$\triangle MNC\cong\triangle ABC$,则$\angle BCM:\angle BCN$等于(D)
A.$1:2$
B.$1:3$
C.$2:3$
D.$1:4$

答案： D 解析:设∠A=3x°,则∠ABC=5x°,∠ACB=10x°.由题意,得3x+5x+10x=180,解得x=10,则∠A=30°,∠ABC=50°,∠ACB=100°.
∴ ∠BCN=180° - 100°=80°.又△MNC≌△ABC，
∴ ∠MCN=∠ACB=100°.
∴ ∠BCM=∠MCN - ∠BCN=100° - 80°=20°.
∴ ∠BCM：∠BCN=20°：80°=1：4.

8. 如图,点$D$、$E$、$F分别在\triangle ABC的边AB$、$BC$、$CA$上(不与顶点重合),设$\angle BAC= \alpha$,$\angle FED= \beta$. 若$\triangle BED\cong\triangle CFE$,则$\alpha与\beta$满足的数量关系是(B)
A.$\alpha+\beta = 90^{\circ}$
B.$\alpha+2\beta = 180^{\circ}$
C.$\alpha-\beta = 90^{\circ}$
D.$2\alpha+\beta = 180^{\circ}$

答案： B 解析:
∵ ∠BAC=α,
∴ ∠B+∠C=180° - α.
∵ △BED≌△CFE，
∴ ∠B=∠C=90° - $\frac{1}{2}$α,∠BDE=∠CEF.
∴ ∠BDE+∠BED=180° - ∠B=180° - $(90° - \frac{1}{2}α)$=90° + $\frac{1}{2}$α.
∴ ∠CEF+∠BED=∠BDE+∠BED=90° + $\frac{1}{2}$α.
∵ ∠FED=β,∠CEF+∠BED+∠FED=180°,
∴ 90° + $\frac{1}{2}$α+β=180°.
∴ α+2β=180°.

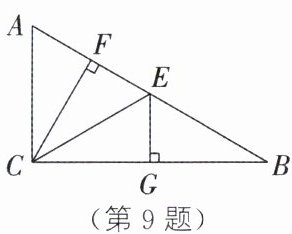
9. 如图,在$\triangle ABC$中,$E是边AB$上的点,$CF\perp AB于点F$,$EG\perp CB于点G$. 如果$\triangle CAF\cong\triangle CEF\cong\triangle CEG\cong\triangle BEG$,那么$\angle ACB$的度数为______90°.

答案： 90° 解析:
∵ △CAF≌△CEF≌△CEG≌△BEG，
∴ ∠ACF=∠ECF=∠ECG=∠B，∠A=∠AEC.
∴ ∠ACB=3∠B.
∵ ∠AEC=∠B+∠ECG=2∠B，
∴ ∠A=2∠B.
∵ ∠A+∠ACB+∠B=180°,
∴ 6∠B=180°.
∴ ∠B=30°.
∴ ∠ACB=90°.

10. 如图,$AB = 12\mathrm{cm}$,$\angle CAB= \angle DBA = 62^{\circ}$,$AC = BD = 9\mathrm{cm}$. 点$P在线段AB上以3\mathrm{cm/s}的速度由点A向点B$运动,同时,点$Q在线段BD上由点B向点D$运动. 设点$Q的运动速度为x\mathrm{cm/s}$. 当以$B$、$P$、$Q为顶点的三角形与\triangle ACP$全等时,$x$的值为3 或$\frac{9}{2}$.

答案： 3 或$\frac{9}{2}$ 解析:设运动时间为t s，则AP=3t cm，BP=(12 - 3t)cm，BQ=xt cm. ① 若△ACP≌△BPQ，则AC=BP,AP=BQ,
∴$\begin{cases} 9=12 - 3t, \\ 3t=xt, \end{cases}$解得$\begin{cases} t=1, \\ x=3. \end{cases}$② 若△ACP≌△BQP,则AC=BQ,AP=BP,
∴$\begin{cases} 9=xt, \\ 3t=12 - 3t, \end{cases}$解得$\begin{cases} t=2, \\ x=\frac{9}{2}. \end{cases}$综上所述，x的值为3或$\frac{9}{2}$.