《2025年拔尖特训八年级数学上册苏科版》

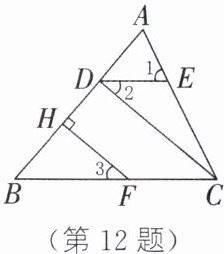
12. 如图,$\angle 1= \angle ACB$,$\angle 2= \angle 3$,$FH\perp AB于点H$。
(1)$\angle 2与\angle DCB$相等吗？为什么？
(2)求证：$CD是\triangle ABC$的高。

答案：
(1) $\angle 2 = \angle DCB$.
∵ $\angle 1 = \angle ACB$，
∴ DE // BC.
∴ $\angle 2 = \angle DCB$.
(2)
∵ $\angle 2 = \angle 3$，$\angle 2 = \angle DCB$，
∴ $\angle 3 = \angle DCB$.
∴ HF // CD.
∴ $\angle CDB = \angle FHB$.
∵ FH⊥AB，
∴ $\angle FHB = 90^{\circ}$.
∴ $\angle CDB = 90^{\circ}$，即 CD⊥AB.
∴ CD 是 $\triangle ABC$ 的高.

13. 某班组织了一次数学活动课,老师让同学们谈谈对三角形相关知识的理解。小峰说：“存在这样一些三角形,它们的三条高之比分别为$1:1:2$,$1:2:3$,$2:3:4$,$3:4:5$。”老师说：“有一个三角形是不存在的。”你认为不存在的三角形的三条高之比是(B)
A.$1:1:2$
B.$1:2:3$
C.$2:3:4$
D.$3:4:5$

答案： B 解析：假设存在这样的三角形. 对于 A，根据等积法，得到此三角形三边长的比为 2:2:1，
∴ 存在这样的三角形. 故 A 不符合题意. 对于 B，同理，可得三边长的比为 6:3:2，这与三角形的三边关系相矛盾，
∴ 这样的三角形不存在. 故 B 符合题意. 对于 C，同理，可得三边长的比为 6:4:3，
∴ 存在这样的三角形. 故 C 不符合题意. 对于 D，同理，可得三边长的比为 20:15:12，
∴ 存在这样的三角形. 故 D 不符合题意.

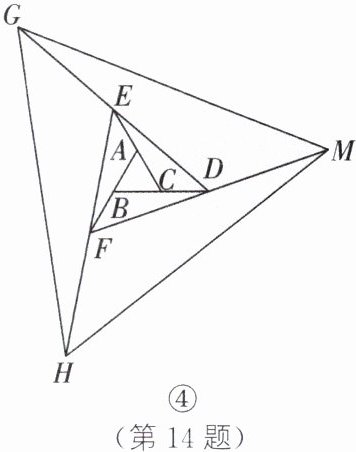
14. 情境题·日常生活 探索：在图①②③中,$\triangle ABC的面积为a$。
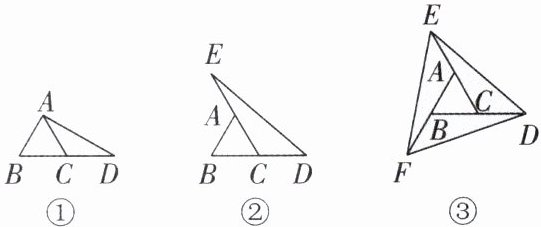
(1)如图①,延长$\triangle ABC的边BC到点D$,使$CD= BC$,连接$DA$。若$\triangle ACD的面积为S_{1}$,则$S_{1}= $______(用含$a$的代数式表示)。
(2)如图②,延长$\triangle ABC的边BC到点D$,延长边$CA到点E$,使$CD= BC$,$AE= CA$,连接$DE$。若$\triangle DEC的面积为S_{2}$,则$S_{2}= $______(用含$a$的代数式表示),并说明理由。
(3)如图③,在图②的基础上延长$AB到点F$,使$BF= AB$,连接$FD$、$FE$,得到$\triangle DEF$。若涂色部分的面积为$S_{3}$,则$S_{3}= $______(用含$a$的代数式表示)。
发现：像上述那样,将$\triangle ABC$各边均顺次延长一倍,连接所得端点,得到$\triangle DEF$(如图③),此时,我们称$\triangle ABC$向外扩展了一次。可以发现,扩展一次后得到的$\triangle DEF的面积是原来\triangle ABC$面积的______倍。
应用：某农户去年在面积为$10m^{2}的三角形空地ABC$上栽种了某种花卉。今年准备扩大种植规模,该农户像上述那样,把$\triangle ABC$向外扩展了两次,第一次由$\triangle ABC扩展成\triangle DEF$,第二次由$\triangle DEF扩展成\triangle MGH$(如图④)。这两次扩展的区域(即涂色部分)的面积共为多少平方米？

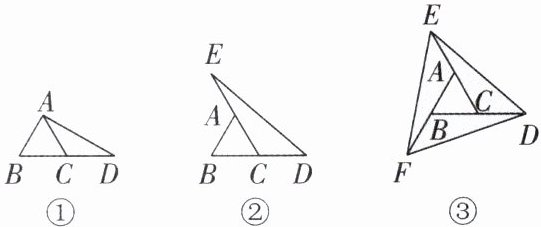
答案：
探索：
(1) a.
(2) 2a. 理由：如图，连接 AD.
∵ CD = BC，AE = CA，
∴ $S_{\triangle DAC}=S_{\triangle DAE}=S_{\triangle ABC}=a$.
∴ $S_2 = 2a$.
(3) 6a. 发现：7. 应用：根据“发现”可知，$S_{\triangle DEF}=7S_{\triangle ABC}=70\ \text{m}^2$，$S_{\triangle MGH}=7S_{\triangle DEF}=490\ \text{m}^2$，
∴ 这两次扩展的区域(即涂色部分)的面积共为 $490 - 10 = 480(\text{m}^2)$.