第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 下列长度的各组线段中,不能构成直角三角形的是(
A.3、3、5
B.3、4、5
C.1、2、$\sqrt {5}$
D.1、$\sqrt {3}$、2
A
)A.3、3、5
B.3、4、5
C.1、2、$\sqrt {5}$
D.1、$\sqrt {3}$、2
答案:
A
2. 一个直角三角形的三边长分别为 a、b、c,那么以 ak、bk、ck(k>0)为三边长的三角形是(
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
A
)A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
答案:
A
3. 如图,在△ABC 中,D 为边 BC 上的一点. 若 AB= 13,AD= 12,AC= 15,BD= 5,则 CD 的长为
9
.
答案:
9
4. 如图,在四边形 ABCD 中,AB⊥BC. 若 AB= 4,BC= 3,AD= 12,CD= 13,则四边形 ABCD 的面积是
36
.
答案:
36
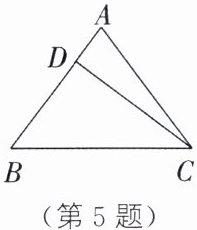
5. 如图,在等腰三角形 ABC 中,AB= AC,BC= 20cm,D 是边 AB 上一点,且 CD= 16cm,BD= 12cm. 求:
(1)AD 的长.
(2)△ABC 的边 BC 上的高.
]
(1)AD 的长.
(2)△ABC 的边 BC 上的高.
]

答案:
(1)
∵ BC=20 cm,CD=16 cm,BD=12 cm,
∴ BD²+CD²=BC².
∴ ∠BDC=90°.
∴ ∠ADC=90°.
设 AD=x cm,则 AC=AB=(x+12)cm.
在Rt△ADC中,由勾股定理,得AD²+CD²=AC²,
∴ x²+16²=(x+12)²,解得x=$\frac{14}{3}$.
∴ AD=$\frac{14}{3}$ cm.
(2)如图,过点A作AE⊥BC于点E,则AE是△ABC的高.
由(1),知AB=AC=$\frac{14}{3}$+12=$\frac{50}{3}$(cm).
∵ AB=AC,AE⊥BC,
∴ BE=CE=$\frac{1}{2}$BC=10 cm.
在Rt△AEB中,由勾股定理,得AE²=AB²-BE²=($\frac{50}{3}$)²-10²=$\frac{1600}{9}$(cm²),
∴ AE=$\frac{40}{3}$ cm,即△ABC的边BC上的高是$\frac{40}{3}$ cm.
∵ BC=20 cm,CD=16 cm,BD=12 cm,
∴ BD²+CD²=BC².
∴ ∠BDC=90°.
∴ ∠ADC=90°.
设 AD=x cm,则 AC=AB=(x+12)cm.
在Rt△ADC中,由勾股定理,得AD²+CD²=AC²,
∴ x²+16²=(x+12)²,解得x=$\frac{14}{3}$.
∴ AD=$\frac{14}{3}$ cm.
(2)如图,过点A作AE⊥BC于点E,则AE是△ABC的高.
由(1),知AB=AC=$\frac{14}{3}$+12=$\frac{50}{3}$(cm).
∵ AB=AC,AE⊥BC,
∴ BE=CE=$\frac{1}{2}$BC=10 cm.
在Rt△AEB中,由勾股定理,得AE²=AB²-BE²=($\frac{50}{3}$)²-10²=$\frac{1600}{9}$(cm²),
∴ AE=$\frac{40}{3}$ cm,即△ABC的边BC上的高是$\frac{40}{3}$ cm.
6. 如图,P 是等边三角形 ABC 内一点,连接 PA、PB、PC,PA:PB:PC= 3:4:5,以 AC 为边在△ABC 外作△AP'C≌△APB,连接 PP',则下列结论错误的是(
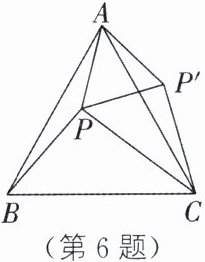
A.△APP'是等边三角形
B.△PCP'是直角三角形
C.∠APB= 150°
D.∠APC= 135°
]
D
)
A.△APP'是等边三角形
B.△PCP'是直角三角形
C.∠APB= 150°
D.∠APC= 135°
]
答案:
D 解析:
∵ △ABC是等边三角形,
∴ ∠BAC=60°.
∵ △AP'C≌△APB,
∴ AP'=AP,P'C=PB,∠P'AC=∠PAB.
∴ 易得∠PAP'=∠BAC=60°.
∴ △APP'是等边三角形.故A正确.又PA:PB:PC=3:4:5,
∴ 设PA=3x,则PP'=PA=3x,P'C=PB=4x,PC=5x.根据勾股定理的逆定理可知,△PCP'是直角三角形,且∠PP'C=90°.故B正确.又△APP'是等边三角形,
∴ ∠AP'P=60°.
∴ 易得∠APB=∠AP'C=150°.故C正确.根据已有的条件无法计算出∠APC的度数.故D错误.
∵ △ABC是等边三角形,
∴ ∠BAC=60°.
∵ △AP'C≌△APB,
∴ AP'=AP,P'C=PB,∠P'AC=∠PAB.
∴ 易得∠PAP'=∠BAC=60°.
∴ △APP'是等边三角形.故A正确.又PA:PB:PC=3:4:5,
∴ 设PA=3x,则PP'=PA=3x,P'C=PB=4x,PC=5x.根据勾股定理的逆定理可知,△PCP'是直角三角形,且∠PP'C=90°.故B正确.又△APP'是等边三角形,
∴ ∠AP'P=60°.
∴ 易得∠APB=∠AP'C=150°.故C正确.根据已有的条件无法计算出∠APC的度数.故D错误.
7. *已知三角形的三边长分别为 a、b、c,且 a+b= 10,ab= 18,c= 8,则该三角形是(
A.等腰三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形
B
)A.等腰三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形
答案:
B 解析:
∵ c=8,
∴ c²=64.
∵ (a+b)²-2ab=100-36=64,
∴ a²+b²=c².
∴ 该三角形是直角三角形.
∵ c=8,
∴ c²=64.
∵ (a+b)²-2ab=100-36=64,
∴ a²+b²=c².
∴ 该三角形是直角三角形.
8. 如图,∠BAC= 90°,AB= 4,AC= 4,BD= 7,DC= 9,则∠DBA 的度数为
45°
.
答案:
45°
9. 如图,在△ABC 中,AB= AC,D 为 AB 上一点,连接 CD,BD= 5,CD= 12,BC= 13,则 AB= ______.
]
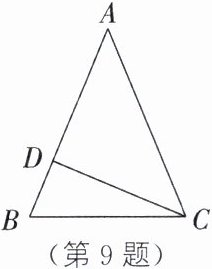
]

16.9
答案:
16.9 解析:在△BDC中,BD=5,CD=12,BC=13.
∴ BD²+CD²=25+144=169,BC²=169.
∴ BD²+CD²=BC².
∴ △BCD是直角三角形,且∠BDC=90°.
∴ ∠ADC=180°-∠BDC=90°.设AB=AC=x,则AD=AB-BD=x-5.在Rt△ADC中,AD²+CD²=AC²,
∴ (x-5)²+144=x²,解得x=16.9.
∴ AB=16.9.
∴ BD²+CD²=25+144=169,BC²=169.
∴ BD²+CD²=BC².
∴ △BCD是直角三角形,且∠BDC=90°.
∴ ∠ADC=180°-∠BDC=90°.设AB=AC=x,则AD=AB-BD=x-5.在Rt△ADC中,AD²+CD²=AC²,
∴ (x-5)²+144=x²,解得x=16.9.
∴ AB=16.9.
查看更多完整答案,请扫码查看


