《2025年拔尖特训八年级数学上册苏科版》

10. 请用尺规在如图所示的数轴上作出表示$\sqrt{13}$对应的点A(保留作图痕迹,不写作法).
]

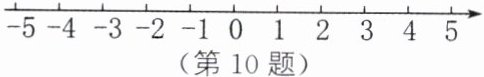
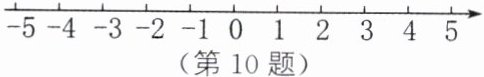
答案：
如图,点 A 即为所求.

11. 如图,在△ABC中,AD⊥BC,垂足为D,BD= 9,AD= 12,CD= 16.
(1)求AC的长.
(2)判断△ABC的形状,并说明理由.
]

答案：
(1)
∵ AD⊥BC,
∴ ∠ADC = 90°.
∵ AD = 12,CD = 16,
∴ $AC = \sqrt{AD^2 + CD^2} = \sqrt{12^2 + 16^2} = 20$,即 AC 的长是 20.
(2)△ABC 是直角三角形.理由:
∵ AD⊥BC,
∴ ∠ADB = 90°.
∵ BD = 9,AD = 12,
∴ $AB = \sqrt{AD^2 + BD^2} = \sqrt{12^2 + 9^2} = 15$.
∵ BD = 9,CD = 16,
∴ BC = BD + CD = 9 + 16 = 25.由
(1)知,AC = 20,
∴ $AC^2 + AB^2 = 20^2 + 15^2 = 400 + 225 = 625 = 25^2 = BC^2$.
∴ △ABC 是直角三角形，且∠BAC = 90°.

12. 如图,在△ABC中,AB= AC= 5,BC= 6,D是边AB上的一个动点,则线段CD长的最小值为______.
]

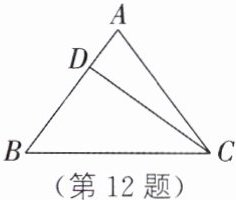
答案：
$\frac{24}{5}$ 解析:如图,过点 A 作 AH⊥BC 于点 H.
∵ AB = AC,
∴ BH = $\frac{1}{2}BC = \frac{1}{2}×6 = 3$. 在 Rt△ABH 中,
∵ ∠AHB = 90°,
∴ 由勾股定理,得$AH^2 = AB^2 - BH^2 = 5^2 - 3^2 = 16$.
∴ AH = 4(负值舍去).由垂线段最短可知,当 CD⊥AB 时,线段 CD 的长取最小值,此时$\frac{1}{2}AB\cdot CD = \frac{1}{2}BC\cdot AH$,即$\frac{1}{2}×5CD = \frac{1}{2}×6×4$,
∴ $CD = \frac{24}{5}$.

13. 拉杆箱是人们出行的常用品,使用拉杆箱可以让人们出行更轻松.如图,某种拉杆箱的箱体长AB= 65cm,拉杆最大伸长距离BC= 35cm,在箱体底端装有一圆形滚轮,当拉杆拉到最长时,滚轮的圆心在图中的点A处,点A到地面的距离AD= 3cm,当拉杆全部缩进箱体时,滚轮圆心水平向右平移55cm到点A'处,求拉杆把手C离地面的距离(假设点C的位置保持不变).
]

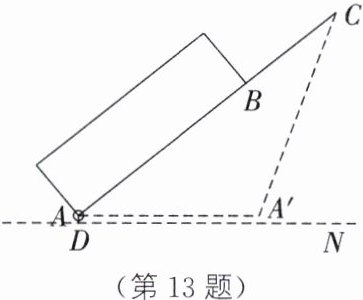
答案：
如图,过点 C 作 CE⊥DN 于点 E,延长 AA'交 CE 于点 F,则∠AFC = 90°.设 A'F = x cm,则 AF = (55 + x)cm.由题意,可得 AC = 65 + 35 = 100(cm),A'C = 65 cm.
∵ 在 Rt△A'CF 中,$CF^2 = A'C^2 - A'F^2$,在 Rt△ACF 中,$CF^2 = AC^2 - AF^2$,
∴ $65^2 - x^2 = 100^2 - (55 + x)^2$,解得 x = 25.
∴ A'F = 25 cm.
∴ $CF = \sqrt{A'C^2 - A'F^2} = 60$cm.又
∵ EF = AD = 3 cm,
∴ CE = 60 + 3 = 63(cm).
∴ 拉杆把手 C 离地面的距离为 63 cm.