《2025年拔尖特训八年级数学上册苏科版》

7. 如图,在平面直角坐标系内,动点 $ P $ 按图中箭头所示的方向依次运动,第 $ 1 $ 次从点 $ (-1,0) $ 运动到点 $ (0,1) $,第 $ 2 $ 次运动到点 $ (1,0) $,第 $ 3 $ 次运动到点 $ (2,-2) … … $ 按这样的运动规律,动点 $ P $ 第 $ 2023 $ 次运动到的点的坐标为 (B)
A.$ (2023,0) $
B.$ (2022,-2) $
C.$ (2023,1) $
D.$ (2022,0) $

答案： B 解析:由题意，可知第1次运动到点(0, 1)、第2次运动到点(1, 0)、第3次运动到点(2, -2)、第4次运动到点(3, 0)、第5次运动到点(4, 1)……
∴动点$P$第$n$次运动到的点的横坐标为$n - 1$，纵坐标每4次为一组循环.
∵2023÷4 = 505(组)……3(次),
∴动点$P$第2023次运动到的点的坐标为(2023 - 1, -2) = (2022, -2).

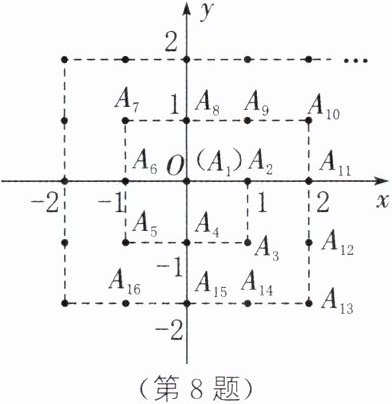
8. 数学家高斯推动了数学学科的发展,被数学界誉为“数学王子”,据传,他在计算 $ 1 + 2 + 3 + 4 + … + 100 $ 时,用到了一种方法,将首尾两个数相加,进而得到 $ 1 + 2 + 3 + 4 + … + 100 = \frac{100 × (1 + 100)}{2} $. 人们借助这样的方法,得到 $ 1 + 2 + 3 + 4 + … + n = \frac{n(1 + n)}{2} $ ($ n $ 是正整数). 如图,在平面直角坐标系中有一系列格点 $ A_i(x_i,y_i) $,其中 $ i = 1 $、$ 2 $、$ 3 $、…$ $、$ n $、…$ $,且 $ x_i $、$ y_i $ 是整数. 记 $ a_n = x_n + y_n $,如 $ A_1(0,0) $,即 $ a_1 = 0 $, $ A_2(1,0) $,即 $ a_2 = 1 $, $ A_3(1,-1) $,即 $ a_3 = 0 $, …$ $,以此类推,则下列结论正确的是 ( B )

A.$ a_{2023} = 40 $
B.$ a_{2024} = 43 $
C.$ a_{(2n - 1)^2} = 2n - 6 $
D.$ a_{(2n - 1)^2} = 2n - 4 $

答案： B 解析:由题图，可得第1层有1个点，即${A}_{1}(0, 0)$，这时${a}_{1} = 0$；第2层有8个点，即点${A}_{2}$到点${A}_{9}(1, 1)$，这时${a}_{9} = 1 + 1 = 2$；第3层有16个点，即点${A}_{10}$到点${A}_{25}(2, 2)$，这时${a}_{25} = 2 + 2 = 4$……以此类推，第$n$层最后一个点为${A}_{{(2n - 1)}^{2}}(n - 1, n - 1)$，即${a}_{{(2n - 1)}^{2}} = 2n - 2$.故选项C、D错误.由规律，可知点${A}_{2025}$在第23层上，且${A}_{2025}(22, 22)$，则${A}_{2023}(20, 22)$，即${a}_{2023} = 20 + 22 = 42$.故选项A错误.点${A}_{2024}$在第23层上，且${A}_{2024}(21, 22)$，即${a}_{2024} = 21 + 22 = 43$.故选项B正确.综上所述，正确的是选项B.

9. $ ^ { \star } $ (2023·恩施宣恩一模) 如图,有一点在第一象限及 $ x $ 轴、$ y $ 轴上运动,它从原点按图中箭头所示的方向运动 [即 $ (0,0) \to (0,1) \to (1,1) \to (1,0) …\to $ ],且每秒运动一个单位长度,则第 $ 2023 $ 秒时这点所在位置的坐标是____.
(1, 44)

答案： (1, 44) 解析:设这点的坐标为$(x, y)$.由题意，可知到点(0, 1)时用了1秒，到点(1, 0)时用了3秒，到点(2, 0)时用了4秒，从点(2, 0)到点(0, 2)有四个单位长度，则到点(0, 2)时用了4 + 4 = 8(秒)，到点(0, 3)时用了9秒；从点(0, 3)到点(3, 0)有六个单位长度，则到点(3, 0)时用了9 + 6 = 15(秒)，以此类推，到点(4, 0)时用了16秒，到点(0, 4)时用了16 + 8 = 24(秒)，到点(0, 5)时用了25秒，到点(5, 0)时用了35秒，到点(6, 0)时用了36秒……
∴在$x$轴上，当横坐标为偶数时，所用时间为${x}^{2}$秒，在$y$轴上，当纵坐标为奇数时，所用时间为${y}^{2}$秒.
∵45×45 = 2025，45为奇数，
∴第2025秒时这点的坐标是(0, 45).
∴第2024秒时这点的坐标是(0, 44).
∴第2023秒时这点的坐标是(1, 44).
方法归纳：确定点运动后的坐标，寻找沿不封闭路线运动的点的坐标规律时，先将图形中的点按照指定的规律、方法动起来，再写出它们对应的坐标，从数的角度感受其变化规律，并求得其中任意一个特殊点的坐标.

10. 如图,在平面直角坐标系中,第一次将 $ \triangle OAB $ 变换成 $ \triangle OA_1B_1 $,第二次将 $ \triangle OA_1B_1 $ 变换成 $ \triangle OA_2B_2 $,第三次将 $ \triangle OA_2B_2 $ 变换成 $ \triangle OA_3B_3 $,顶点坐标分别为 $ A(1,3) $、$ A_1(-2,-3) $、$ A_2(4,3) $、$ A_3(-8,-3) $、$ B(2,0) $、$ B_1(-4,0) $、$ B_2(8,0) $、$ B_3(-16,0) $.
(1) 观察每次变换前后的三角形有何变化,找出其中的规律,按此变化规律再将 $ \triangle OA_3B_3 $ 变换成 $ \triangle OA_4B_4 $,则点 $ A_4 $ 的坐标为(16, 3),点 $ B_4 $ 的坐标为(32, 0).
(2) 若按 (1) 中找到的规律将 $ \triangle OAB $ 进行了 $ n $ 次变换,得到 $ \triangle OA_nB_n $,求点 $ A_n $、$ B_n $ 的坐标.
∵点$A$的坐标为(1, 3)，点${A}_{1}$的坐标为(-2, -3)，即$({(-1)}^{1}×{2}^{1}, {(-1)}^{1}×3)$，点${A}_{2}$的坐标为(4, 3)，即$({(-1)}^{2}×{2}^{2}, {(-1)}^{2}×3)$……
∴易知点${A}_{n}$的坐标为$({(-1)}^{n}·{2}^{n}, {(-1)}^{n}·3)$.
∵点$B$的坐标为(2, 0)，点${B}_{1}$的坐标为(-4, 0)，即$({(-1)}^{1}×{2}^{2}, 0)$,点${B}_{2}$的坐标为(8, 0)，即$({(-1)}^{2}×{2}^{3}, 0)$……
∴易知点${B}_{n}$的坐标为$({(-1)}^{n}·{2}^{n + 1}, 0)$.

答案：
(1)(16, 3);(32, 0).
(2)
∵点$A$的坐标为(1, 3)，点${A}_{1}$的坐标为(-2, -3)，即$({(-1)}^{1}×{2}^{1}, {(-1)}^{1}×3)$，点${A}_{2}$的坐标为(4, 3)，即$({(-1)}^{2}×{2}^{2}, {(-1)}^{2}×3)$……
∴易知点${A}_{n}$的坐标为$({(-1)}^{n}·{2}^{n}, {(-1)}^{n}·3)$.
∵点$B$的坐标为(2, 0)，点${B}_{1}$的坐标为(-4, 0)，即$({(-1)}^{1}×{2}^{2}, 0)$,点${B}_{2}$的坐标为(8, 0)，即$({(-1)}^{2}×{2}^{3}, 0)$……
∴易知点${B}_{n}$的坐标为$({(-1)}^{n}·{2}^{n + 1}, 0)$.