第98页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
1. (济宁嘉祥县期末)在直角三角形中,若股为4,弦为5,则勾为(
A.3
B.5
C.9
D.6
A
)A.3
B.5
C.9
D.6
答案:
1.A
2. 如图,点E在正方形ABCD的边AB上.若EB=1,EC=2,则正方形ABCD的面积为(
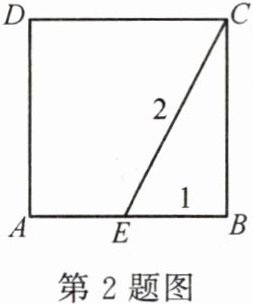
A.2
B.3
C.4
D.5
B
)
A.2
B.3
C.4
D.5
答案:
2.B
3. 在△ABC中,∠A=25°,∠B=65°,则下列式子成立的是(
A.AC²+BC²=AB²
B.AB²+BC²=AC²
C.AC²-BC²=AB²
D.AC²+AB²=BC²
A
)A.AC²+BC²=AB²
B.AB²+BC²=AC²
C.AC²-BC²=AB²
D.AC²+AB²=BC²
答案:
3.A
4. 直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为(
A.4
B.6
C.8
D.10
D
)A.4
B.6
C.8
D.10
答案:
4.D
5. (临沂蒙阴县期末)如图,在△ABC中,AB=AC,AD⊥BC.若AB=5,BC=8,则AD的长为(
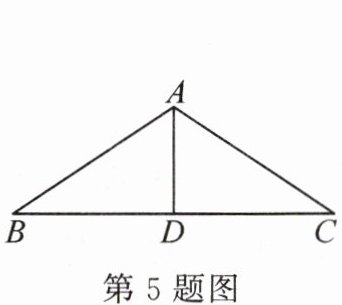
A.3
B.4
C.$\frac{3}{2}$
D.7
A
)
A.3
B.4
C.$\frac{3}{2}$
D.7
答案:
5.A
6. (德州乐陵市期中)已知直角三角形两直角边分别为5 cm,12 cm,则其斜边上的高的长度为(
A.6 cm
B.8 cm
C.$\frac{80}{13}$ cm
D.$\frac{60}{13}$ cm
D
)A.6 cm
B.8 cm
C.$\frac{80}{13}$ cm
D.$\frac{60}{13}$ cm
答案:
6.D
7. 在Rt△ABC中,∠C=90°.
(1)若a=12,b=16,则c=
(2)若b=8,c=17,则a=
(1)若a=12,b=16,则c=
20
;(2)若b=8,c=17,则a=
15
.
答案:
7.
(1)20
(2)15
(1)20
(2)15
8. 新考向 真实情境 一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以到达该建筑物的最大高度是
12
米.
答案:
8.12
9. 如图,已知一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距

40
海里.
答案:
9.40
10. 如图,两棵树的高分别为10米和4米,相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则该小鸟至少飞行

10
米.
答案:
10.10
11. 某同学学习了“勾股定理”之后,为了测量如图所示的风筝的高度CE,测得如下数据:
①BD的长度为8米(注:BD⊥CE);②放出的风筝线BC的长为17米;③牵线放风筝的同学身高为1.60米.
(1)求风筝的高度CE;
(2)若该同学想让风筝沿CD方向下降9米,则他应该往回收线多少米?
 ]
]
①BD的长度为8米(注:BD⊥CE);②放出的风筝线BC的长为17米;③牵线放风筝的同学身高为1.60米.
(1)求风筝的高度CE;
(2)若该同学想让风筝沿CD方向下降9米,则他应该往回收线多少米?
 ]
]
答案:
11.解:
(1)在Rt△CDB中,由勾股定理,得$CD^{2}=BC^{2}-BD^{2}=17^{2}-8^{2}=225$,所以$CD=15$(负值舍去).所以$CE=CD + DE=15 + 1.6=16.6$(米).答:风筝的高度$CE$为16.6米.
(2)在$CD$上取一点$M$,使$CM = 9$米,连接$BM$.所以$DM=CD - CM=15 - 9 = 6$(米).因为$BM^{2}=DM^{2}+BD^{2}=6^{2}+8^{2}=100=10^{2}$,所以$BM = 10$米.所以$BC - BM=7$米.所以他应该往回收线7米.
(1)在Rt△CDB中,由勾股定理,得$CD^{2}=BC^{2}-BD^{2}=17^{2}-8^{2}=225$,所以$CD=15$(负值舍去).所以$CE=CD + DE=15 + 1.6=16.6$(米).答:风筝的高度$CE$为16.6米.
(2)在$CD$上取一点$M$,使$CM = 9$米,连接$BM$.所以$DM=CD - CM=15 - 9 = 6$(米).因为$BM^{2}=DM^{2}+BD^{2}=6^{2}+8^{2}=100=10^{2}$,所以$BM = 10$米.所以$BC - BM=7$米.所以他应该往回收线7米.
查看更多完整答案,请扫码查看


