第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. (2024·贵州)如图,在扇形纸扇中,若$∠AOB=150^{\circ },OA=24$,则$\widehat {AB}$的长为 (

A. $30π$B. $25π$
C. $20π$D. $10π$
【变式】(2024·四川绵阳)将一把折扇展开,可抽象成一个扇形,若该扇形的半径为2,弧长为$\frac {4π}{3}$,则扇形的圆心角大小为 (
A. $30^{\circ }$
B. $60^{\circ }$
C. $90^{\circ }$
D. $120^{\circ }$
C
)
A. $30π$B. $25π$
C. $20π$D. $10π$
【变式】(2024·四川绵阳)将一把折扇展开,可抽象成一个扇形,若该扇形的半径为2,弧长为$\frac {4π}{3}$,则扇形的圆心角大小为 (
D
)A. $30^{\circ }$
B. $60^{\circ }$
C. $90^{\circ }$
D. $120^{\circ }$
答案:
1. C 【变式】D
2. 如图,在$Rt△ABC$中,$∠C=90^{\circ },∠B=30^{\circ },AB=8$,以点C为圆心,CA的长为半径画弧,交AB于点D,则$\widehat {AD}$的长为 (
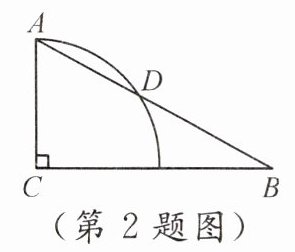
A. $π$
B. $\frac {4}{3}π$
C. $\frac {5}{3}π$
D. $2π$
B
)
A. $π$
B. $\frac {4}{3}π$
C. $\frac {5}{3}π$
D. $2π$
答案:
2. B
3. (2024·江苏镇江)如图,四边形ABCD为平行四边形,以点A为圆心,AB长为半径画弧,交BC边于点E,连接AE,$AB=1,∠D=60^{\circ }$,则$\widehat {BE}$的长$l=$

$\frac{1}{3}\pi$
.(结果保留π)
答案:
3. $\frac{1}{3}\pi$
4. 跨学科 物理 如图,用一个半径为6 cm的定滑轮拉动重物上升,滑轮旋转了$120^{\circ }$,假设绳索粗细不计,且与轮滑之间没有滑动,则重物上升了

$4\pi$
cm.(结果保留π)
答案:
4. $4\pi$
5. 半径为4,圆心角为$90^{\circ }$的扇形的面积(结果保留π)为 (
A. $2π$
B. $3π$
C. $4π$
D. $6π$
C
)A. $2π$
B. $3π$
C. $4π$
D. $6π$
答案:
5. C
6. (2024·山东青岛)如图,A,B,C,D是$\odot O$上的点,半径$OA=3,\widehat {AB}=\widehat {CD},∠DBC=25^{\circ }$,连接AD,则扇形AOB的面积为 (

A. $\frac {5}{4}π$
B. $\frac {5}{8}π$
C. $\frac {5}{2}π$
D. $\frac {5}{12}π$
A
)
A. $\frac {5}{4}π$
B. $\frac {5}{8}π$
C. $\frac {5}{2}π$
D. $\frac {5}{12}π$
答案:
6. A
7. (2024·广东深圳)如图,小明在矩形ABCD中裁剪出扇形EOF,$BC=\sqrt {2}AB$,O为BC中点,$OE=AB=4$,则扇形EOF的面积为____

4π
.
答案:
7. $4\pi$
8. 数学思想 整体思想 如图,$\odot A,\odot B,\odot C$两两不相交,且半径都等于2,则图中三个扇形(即阴影部分)的面积之和为

$2\pi$
.(结果保留π)
答案:
8. $2\pi$
9. 如图,已知菱形ABCD的边长为1.5 cm,B,C两点在扇形AEF的$\widehat {EF}$上,求$\widehat {BC}$的长度为
$\frac{1}{2}\pi$ cm
及扇形ABC的面积为$\frac{3}{8}\pi$ $cm^{2}$
.
答案:
9. 解:
∵ 四边形 ABCD 是菱形且边长为 1.5 cm,
∴ $AB = BC = 1.5$ cm. 又
∵ B,C 两点在扇形 AEF 的 $\overset{\frown}{EF}$ 上,
∴ $AB = BC = AC = 1.5$ cm,
∴ $\triangle ABC$ 是等边三角形,
∴ $\angle BAC = 60^{\circ}$,
∴ $l_{\overset{\frown}{BC}} = \frac{60\pi \times 1.5}{180} = \frac{1}{2}\pi$ (cm),$S_{扇形ABC} = \frac{60\pi \times 1.5^{2}}{360} = \frac{3}{8}\pi$ ($cm^{2}$).
∵ 四边形 ABCD 是菱形且边长为 1.5 cm,
∴ $AB = BC = 1.5$ cm. 又
∵ B,C 两点在扇形 AEF 的 $\overset{\frown}{EF}$ 上,
∴ $AB = BC = AC = 1.5$ cm,
∴ $\triangle ABC$ 是等边三角形,
∴ $\angle BAC = 60^{\circ}$,
∴ $l_{\overset{\frown}{BC}} = \frac{60\pi \times 1.5}{180} = \frac{1}{2}\pi$ (cm),$S_{扇形ABC} = \frac{60\pi \times 1.5^{2}}{360} = \frac{3}{8}\pi$ ($cm^{2}$).
查看更多完整答案,请扫码查看


