第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
10. 新视角 动点探究题 如图,在矩形$ABCD$中,$AB=18cm$,$AD=4cm$,点$P$,$Q$分别从$A$,$B$同时出发,点$P$在$AB$边上沿$AB$方向以$2cm/s$的速度运动,点$Q$在$BC$边上沿$BC$方向以$1cm/s$的速度运动. 当其中一个点停止运动时,另一个点也停止运动. 设运动时间为$xs$,$\triangle PBQ$的面积为$ycm^{2}$.
(1)求$y$关于$x$的函数关系式,并指出$x$的取值范围;
(2)运动多长时间后$\triangle PBQ$的面积最大?最大面积是多少?
(1)$y$关于$x$的函数关系式为
(2)运动
(1)求$y$关于$x$的函数关系式,并指出$x$的取值范围;
(2)运动多长时间后$\triangle PBQ$的面积最大?最大面积是多少?
(1)$y$关于$x$的函数关系式为
$y=-x^2 + 9x$
,$x$的取值范围为$0 \leq x \leq 4$
;(2)运动
4
s后$\triangle PBQ$的面积最大,最大面积是20
$cm^{2}$.
答案:
解:
(1)$\because PB = AB - AP = (18 - 2x)$cm,$BQ = x$cm,$\therefore y = \frac{1}{2}(18 - 2x) \cdot x = -x^2 + 9x$,x的取值范围为$0 \leq x \leq 4$;
(2)$y = -x^2 + 9x = -(x - \frac{9}{2})^2 + \frac{81}{4}$。$\because -1 < 0$,$\therefore$此抛物线的开口向下,$\therefore$当$0 \leq x \leq 4$时,y随x的增大而增大,$\therefore$当$x = 4$时,y最大,$y_{最大} = -4^2 + 9 \times 4 = 20$。$\therefore$运动4 s后$\triangle PBQ$的面积最大,最大面积为20 cm²。
(1)$\because PB = AB - AP = (18 - 2x)$cm,$BQ = x$cm,$\therefore y = \frac{1}{2}(18 - 2x) \cdot x = -x^2 + 9x$,x的取值范围为$0 \leq x \leq 4$;
(2)$y = -x^2 + 9x = -(x - \frac{9}{2})^2 + \frac{81}{4}$。$\because -1 < 0$,$\therefore$此抛物线的开口向下,$\therefore$当$0 \leq x \leq 4$时,y随x的增大而增大,$\therefore$当$x = 4$时,y最大,$y_{最大} = -4^2 + 9 \times 4 = 20$。$\therefore$运动4 s后$\triangle PBQ$的面积最大,最大面积为20 cm²。
11. 新趋势 学科内综合 (2024·广东肇庆一模)
【发现问题】
由$(a-b)^{2}≥0$,得$a^{2}+b^{2}≥2ab$. 如果两个正数$a$,$b$,即$a>0$,$b>0$,则有下面的不等式:$a+b≥2\sqrt {ab}$,当且仅当$a=b$时取到等号.
【提出问题】
若$a>0$,$b>0$,利用配方能否求出$a+b$的最小值呢?
【分析问题】
例如:已知$x>0$,求式子$x+\frac {4}{x}$的最小值.
解:令$a=x$,$b=\frac {4}{x}$,则由$a+b≥2\sqrt {ab}$,得$x+\frac {4}{x}≥2\sqrt {x\cdot \frac {4}{x}}=4$,当且仅当$x=\frac {4}{x}$时,即$x=2$时,式子有最小值,最小值为$4$.
【解决问题】
请根据上面材料解答下列问题:
(1)$2+3$
【能力提升】
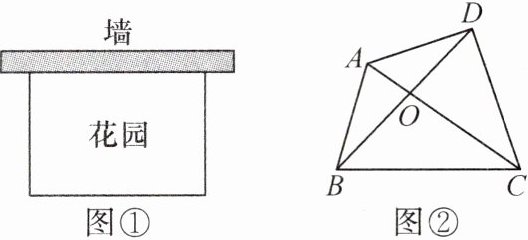
(2)如图①,用篱笆围一个面积为$32m^{2}$的长方形花园,使这个长方形花园的一边靠墙(墙长$20m$),问这个长方形的长、宽各为多少时,所用的篱笆最短,最短的篱笆是多少?
(3)如图②,四边形$ABCD$的对角线$AC$,$BD$相交于点$O$,$\triangle AOB$,$\triangle COD$的面积分别是$8$和$14$,求四边形$ABCD$面积的最小值.
【发现问题】
由$(a-b)^{2}≥0$,得$a^{2}+b^{2}≥2ab$. 如果两个正数$a$,$b$,即$a>0$,$b>0$,则有下面的不等式:$a+b≥2\sqrt {ab}$,当且仅当$a=b$时取到等号.
【提出问题】
若$a>0$,$b>0$,利用配方能否求出$a+b$的最小值呢?
【分析问题】
例如:已知$x>0$,求式子$x+\frac {4}{x}$的最小值.
解:令$a=x$,$b=\frac {4}{x}$,则由$a+b≥2\sqrt {ab}$,得$x+\frac {4}{x}≥2\sqrt {x\cdot \frac {4}{x}}=4$,当且仅当$x=\frac {4}{x}$时,即$x=2$时,式子有最小值,最小值为$4$.
【解决问题】
请根据上面材料解答下列问题:
(1)$2+3$
>
$2\sqrt {2×3}$(选填“>”“<”或“=”);当$x>0$,式子$x+\frac {1}{x}$的最小值为2
;【能力提升】
(2)如图①,用篱笆围一个面积为$32m^{2}$的长方形花园,使这个长方形花园的一边靠墙(墙长$20m$),问这个长方形的长、宽各为多少时,所用的篱笆最短,最短的篱笆是多少?
(3)如图②,四边形$ABCD$的对角线$AC$,$BD$相交于点$O$,$\triangle AOB$,$\triangle COD$的面积分别是$8$和$14$,求四边形$ABCD$面积的最小值.

答案:
解:
(1)$>$ 2
(2)设这个长方形花园靠墙的一边的长为x m,另一边为y m。根据题意,得$xy = 32$,$\therefore y = \frac{32}{x}$,$\therefore$这个篱笆的长为$\frac{32}{x} \times 2 + x = (\frac{64}{x} + x)$m。根据材料可得,$\frac{64}{x} + x \geq 2\sqrt{\frac{64}{x} \times x}$,当且仅当$\frac{64}{x} = x$时,即$x = 8$时取等号,$\therefore y = \frac{32}{x} = \frac{32}{8} = 4$,$\frac{64}{x} + x = 8 + 8 = 16$,$\therefore$当长、宽分别为8 m,4 m时,所用的篱笆最短,最短的篱笆是16 m;
(3)设$S_{\triangle BOC} = x$,已知$S_{\triangle AOB} = 8$,$S_{\triangle COD} = 14$,则由等高三角形可知:$S_{\triangle BOC} : S_{\triangle COD} = BO : OD = S_{\triangle AOB} : S_{\triangle AOD}$,$\therefore x : 14 = 8 : S_{\triangle AOD}$,$\therefore S_{\triangle AOD} = \frac{112}{x}$,$\therefore$四边形ABCD面积为$8 + 14 + x + \frac{112}{x} \geq 22 + 2\sqrt{x \times \frac{112}{x}} = 22 + 8\sqrt{7}$,当且仅当$x = \frac{112}{x}$,即$x = 4\sqrt{7}$时,取等号,$\therefore$四边形ABCD面积的最小值为$22 + 8\sqrt{7}$。
(1)$>$ 2
(2)设这个长方形花园靠墙的一边的长为x m,另一边为y m。根据题意,得$xy = 32$,$\therefore y = \frac{32}{x}$,$\therefore$这个篱笆的长为$\frac{32}{x} \times 2 + x = (\frac{64}{x} + x)$m。根据材料可得,$\frac{64}{x} + x \geq 2\sqrt{\frac{64}{x} \times x}$,当且仅当$\frac{64}{x} = x$时,即$x = 8$时取等号,$\therefore y = \frac{32}{x} = \frac{32}{8} = 4$,$\frac{64}{x} + x = 8 + 8 = 16$,$\therefore$当长、宽分别为8 m,4 m时,所用的篱笆最短,最短的篱笆是16 m;
(3)设$S_{\triangle BOC} = x$,已知$S_{\triangle AOB} = 8$,$S_{\triangle COD} = 14$,则由等高三角形可知:$S_{\triangle BOC} : S_{\triangle COD} = BO : OD = S_{\triangle AOB} : S_{\triangle AOD}$,$\therefore x : 14 = 8 : S_{\triangle AOD}$,$\therefore S_{\triangle AOD} = \frac{112}{x}$,$\therefore$四边形ABCD面积为$8 + 14 + x + \frac{112}{x} \geq 22 + 2\sqrt{x \times \frac{112}{x}} = 22 + 8\sqrt{7}$,当且仅当$x = \frac{112}{x}$,即$x = 4\sqrt{7}$时,取等号,$\therefore$四边形ABCD面积的最小值为$22 + 8\sqrt{7}$。
查看更多完整答案,请扫码查看


