《2025年名师测控九年级数学上册人教版》

1. 下列说法不正确的是 (D)
A. 正多边形一定有一个外接圆和一个内切圆
B. 各边相等且各角相等的多边形是正多边形
C. 正多边形的内切圆和外接圆是同心圆
D. 正多边形既是轴对称图形,又是中心对称图形

答案： 1.D

2. 若一个正多边形的中心角是$72^{\circ }$,则这个正多边形的边数是 (B)
A. 4
B. 5
C. 6
D. 7

答案： 2.B

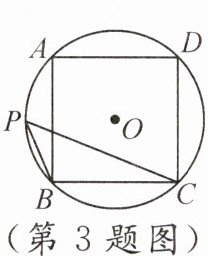
3. 如图,正方形 ABCD 内接于$\odot O$,点 P 在$\widehat {AB}$上,则$∠BPC$的度数为 (B)

A. $30^{\circ }$
B. $45^{\circ }$
C. $60^{\circ }$
D. $90^{\circ }$

答案： 3.B

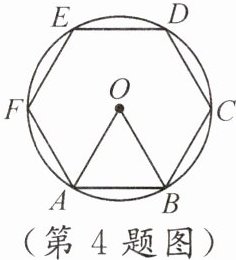
4. (2024·四川甘孜州)如图,正六边形 ABCDEF 内接于$\odot O,OA=1$,则 AB 的长为 (C)

A. 2
B. $\sqrt {3}$
C. 1
D. $\frac {1}{2}$

答案： 4.C

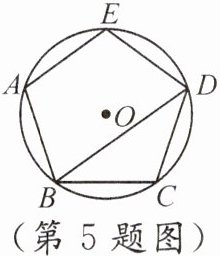
5. 如图,已知正五边形 ABCDE 内接于$\odot O$,连接 BD,则$∠ABD$的度数是 (C)

A. $60^{\circ }$
B. $70^{\circ }$
C. $72^{\circ }$
D. $114^{\circ }$

答案： 5.C

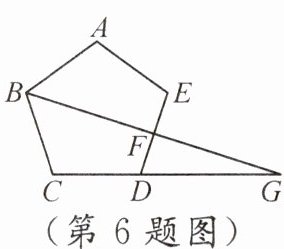
6. (2024·四川广元)如图,点 F 是正五边形 ABCDE 边 DE 的中点,连接 BF 并延长,与 CD 延长线交于点 G,则$∠BGC$的度数为____18°.

答案： 6.18°

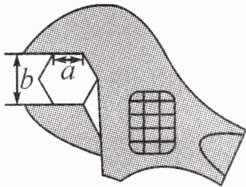
7. 情境题 拧螺帽 如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度$b=3cm$,则螺帽边长$a=$$\sqrt{3}$cm.

答案： 7.$\sqrt{3}$

8. 如图,正六边形 ABCDEF 内接于$\odot O$,若$\odot O$的内接正三角形 ACE 的面积为$48\sqrt {3}$,求正六边形的周长.

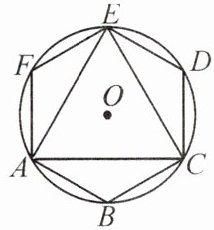
解:过点O作OH⊥AC于点H,连接OA,则∠OAH=30°.在Rt△OAH中,设OA=R,则OH=$\frac{1}{2}$R,由勾股定理，得AH=$\sqrt{OA^{2} - OH^{2}} = \sqrt{R^{2} - (\frac{1}{2}R)^{2}} = \frac{\sqrt{3}}{2}R$。∴$S_{\triangle ACE} = 6S_{\triangle OAH} = 6 × \frac{1}{2}AH \cdot OH = 6 × \frac{1}{2} × \frac{\sqrt{3}}{2}R × \frac{1}{2}R = \frac{3\sqrt{3}}{4}R^{2} = 48\sqrt{3}$，解得R=8。即正六边形的边长为8,∴正六边形的周长为6×8=48。

答案： 8.解:过点O作OH⊥AC于点H,连接OA,则∠OAH=30°.在Rt△OAH中,设OA=R,则OH=$\frac{1}{2}$R,由勾股定理，得AH=$\sqrt{OA^{2} - OH^{2}} = \sqrt{R^{2} - (\frac{1}{2}R)^{2}} = \frac{\sqrt{3}}{2}R$。
∴$S_{\triangle ACE} = 6S_{\triangle OAH} = 6 \times \frac{1}{2}AH \cdot OH = 6 \times \frac{1}{2} \times \frac{\sqrt{3}}{2}R \times \frac{1}{2}R = \frac{3\sqrt{3}}{4}R^{2} = 48\sqrt{3}$，解得R=8。即正六边形的边长为8,
∴正六边形的周长为6×8=48。

9. 图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形. 如图②,AE 是$\odot O$的直径,用直尺和圆规作$\odot O$的内接正八边形 ABCDEFGH. (不写作法,保留作图痕迹)

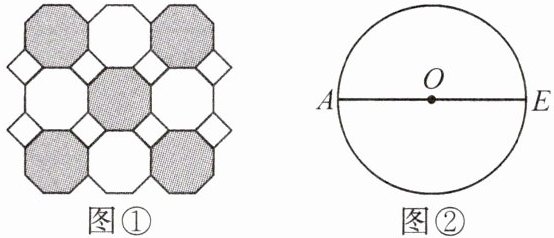
答案：
9.解:如图.

10. 若 AB 是$\odot O$的内接正五边形的一边,AC 是$\odot O$的内接正六边形的一边,则$∠BAC$的度数为6°或114°.

答案： 10.6°或114°