第97页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
11. 情境题 蜂巢 蜂巢结构精巧,其巢房横截面的形状均为正六边形. 如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点 P,Q,M 均为正六边形的顶点. 若点 P,Q 的坐标分别为$(-2\sqrt {3},3),(0,-3)$,则点 M 的坐标为 (
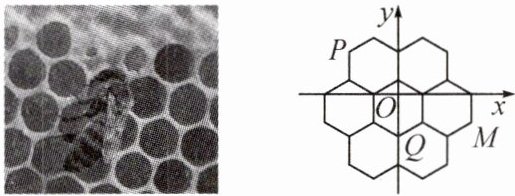
A. $(3\sqrt {3},-2)$
B. $(3\sqrt {3},2)$
C. $(2,-3\sqrt {3})$
D. $(-2,-3\sqrt {3})$
A
)
A. $(3\sqrt {3},-2)$
B. $(3\sqrt {3},2)$
C. $(2,-3\sqrt {3})$
D. $(-2,-3\sqrt {3})$
答案:
11.A
12. (2024·山东济宁)如图,边长为 2 的正六边形 ABCDEF 内接于$\odot O$,则它的内切圆半径为 (
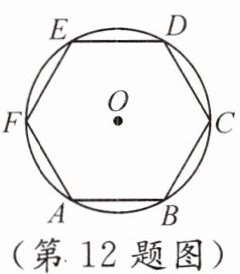
A. 1
B. 2
C. $\sqrt {2}$
D. $\sqrt {3}$
D
)
A. 1
B. 2
C. $\sqrt {2}$
D. $\sqrt {3}$
答案:
12.D
13. 如图,正五边形 ABCDE 和正三角形 AMN 都是$\odot O$的内接多边形,则$∠BOM$的度数为____
48°
.
答案:
13.48°
14. 如图,正方形 ABCD 和正三角形 AEF 内接于$\odot O$,连接 BE. 试判断:BE 是$\odot O$内接正
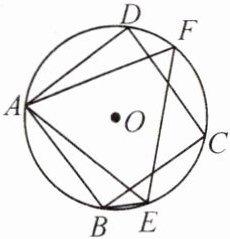
十二
边形的边长,并说明理由.
答案:
14.解:BE是⊙O内接正十二边形的边长.理由如下:连接OA,OB,OE,则∠AOE=$\frac{360^{\circ}}{3} = 120^{\circ}$,∠AOB=$\frac{360^{\circ}}{4} = 90^{\circ}$,
∴∠BOE=∠AOE−∠AOB=120°−90°=30°,
∵360°÷30°=12,
∴BE是⊙O内接正十二边形的边长。
∴∠BOE=∠AOE−∠AOB=120°−90°=30°,
∵360°÷30°=12,
∴BE是⊙O内接正十二边形的边长。
15. 新考法 规律探究题 如图①②③…n,M,N 分别是$\odot O$的内接正三角形 ABC,正方形 ABCD,正五边形 ABCDE……正n边形 ABCDEF…的边 AB,BC 上的点,且$BM=CN$,连接 OM,ON.
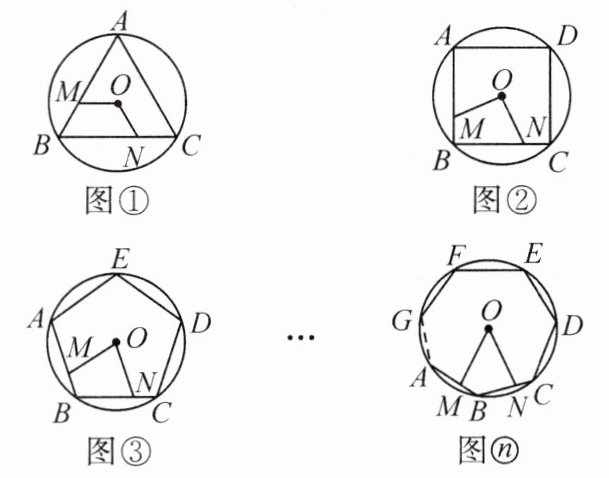
(1)求图①中$∠MON$的度数;
(2)图②中$∠MON$的度数是
(3)试探究$∠MON$的度数与正n边形边数n的关系.(直接写出答案)

(1)求图①中$∠MON$的度数;
(2)图②中$∠MON$的度数是
90°
,图③中$∠MON$的度数是72°
;(3)试探究$∠MON$的度数与正n边形边数n的关系.(直接写出答案)
答案:
15.解:
(1)连接OB,OC.
∵正三角形ABC内接于⊙O,
∴OB=OC,∠BOC=120°,
∴∠OBC=∠OCB=30°,
∴∠OBM=60°−30°=30°,
∴∠OBM=∠OCN。又
∵BM=CN,OB=OC,
∴△BOM≌△CON(SAS),
∴∠BOM=∠CON,
∴∠BOM+∠BON=∠CON+∠BON,
∴∠MON=∠BOC=120°;
(2)90° 72°
(3)∠MON=$\frac{360^{\circ}}{n}$。
(1)连接OB,OC.
∵正三角形ABC内接于⊙O,
∴OB=OC,∠BOC=120°,
∴∠OBC=∠OCB=30°,
∴∠OBM=60°−30°=30°,
∴∠OBM=∠OCN。又
∵BM=CN,OB=OC,
∴△BOM≌△CON(SAS),
∴∠BOM=∠CON,
∴∠BOM+∠BON=∠CON+∠BON,
∴∠MON=∠BOC=120°;
(2)90° 72°
(3)∠MON=$\frac{360^{\circ}}{n}$。
查看更多完整答案,请扫码查看


