《2025年名师测控九年级数学上册人教版》

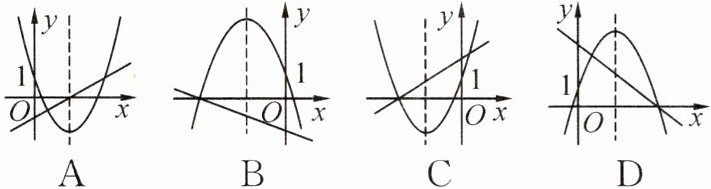
1. 二次函数$y = ax^{2}+bx + 1$的图象与一次函数$y = 2ax + b$在同一平面直角坐标系中的图象可能是（A）

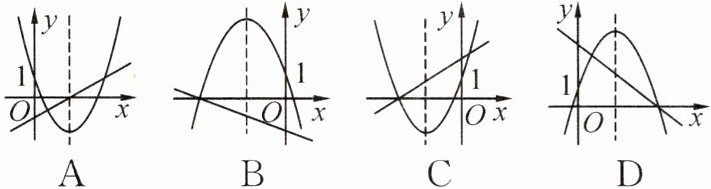
答案： A

2. 抛物线$y=\frac {2}{3}(x - 1)^{2}+c$经过$(-2,y_{1})$，$(0,y_{2})$，$(\frac {5}{2},y_{3})$三点，则$y_{1}$，$y_{2}$，$y_{3}$的大小关系正确的是（D）
A. $y_{1}＞y_{2}＞y_{3}$
B. $y_{2}＞y_{3}＞y_{1}$
C. $y_{3}＞y_{1}＞y_{2}$
D. $y_{1}＞y_{3}＞y_{2}$

答案： D

3. 将抛物线$y = x^{2}-4x + 5$向左平移1个单位长度，再向下平移2个单位长度后得到的抛物线的顶点坐标为$(1,-1)$。

答案： $(1,-1)$

4. (2024·广州越秀区校级三模)若抛物线$y = x^{2}-2x + ax + 2$的对称轴是$y$轴，则$a$的值是____2。

答案： 2

5. (2024·湖北)已知抛物线$y = ax^{2}+bx + c$（$a$，$b$，$c$为常数，$a\neq0$）的顶点坐标为$(-1,-2)$，与$y$轴的交点在$x$轴上方，下列结论正确的是（C）
A. $a＜0$
B. $c＜0$
C. $a - b + c=-2$
D. $b^{2}-4ac = 0$

答案： C

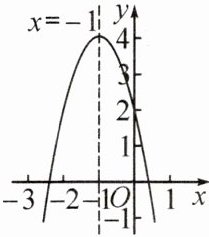
6. 已知二次函数$y = ax^{2}+bx + c$（$a\neq0$）的部分图象如图所示，图象经过点$(0,2)$，其对称轴为直线$x=-1$。下列结论：①$3a + c＞0$；②若点$(-4,y_{1})$，$(3,y_{2})$均在二次函数图象上，则$y_{1}＞y_{2}$；③关于$x$的一元二次方程$ax^{2}+bx + c=-1$有两个相等的实数根；④满足$ax^{2}+bx + c＞2$的$x$的取值范围为$-2＜x＜0$。其中，正确结论的个数为（B）

A. 1
B. 2
C. 3
D. 4

答案： B

7. (2024·山东烟台)每年5月的第三个星期日为全国助残日，今年的主题是“科技助残，共享美好生活”。康宁公司新研发了一批便携式轮椅，计划在该月销售。根据市场调查，每辆轮椅盈利200元时，每天可售出60辆；单价每降低10元，每天可多售出4辆。公司决定在成本不变的情况下降价销售，但每辆轮椅的利润不低于180元。设每辆轮椅降价$x$元，每天的销售利润为$y$元。
(1)求$y$与$x$的函数关系式；每辆轮椅降价多少元时，每天的销售利润最大？最大利润为多少元？
(2)全国助残日当天，公司共获得销售利润12160元，请问这天售出了多少辆轮椅？

答案： 解:
(1) $y=(200-x)\left(60+4 \times \frac{x}{10}\right)= -0.4 x^{2}+20 x+12000=-0.4(x-25)^{2}+12250 . \because-0.4＜0, \therefore$ 此抛物线开口向下. $\because 200-x \geqslant 180, \therefore x \leqslant 20 . \therefore$ 当 $x=20$ 时, 利润最大, 最大利润为 $-0.4 \times(20-25)^{2}+ 12250=12240 . \therefore y$ 与 $x$ 的函数关系式为 $y=-0.4 x^{2}+20 x+12000$; 每辆轮椅降价 20 元时, 每天的销售利润最大, 最大利润为 12240 元;
(2) 根据题意, 得 $12160= -0.4(x-25)^{2}+12250$. 解得 $x_{1}=40$ (不合题意, 舍去), $x_{2}=10 . \therefore$ 售出轮椅的数量为 $60+4 \times \frac{10}{10}=64$ (辆). 答: 这天售出了 64 辆轮椅.