第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
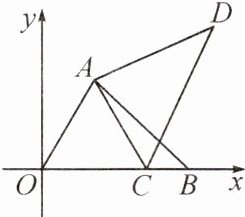
9. 如图,在$△OAB$中,$∠AOB=60^{\circ },OA=4$,点B的坐标为(6,0).将$△OAB$绕点A逆时针旋转得到$△CAD$.当点O的对应点C落在OB上时,点D的坐标为 (
A. (7,$3\sqrt {3}$)
B. (7,5)
C. ($5\sqrt {3}$,5)
D. ($5\sqrt {3}$,$3\sqrt {3}$)
A
)
A. (7,$3\sqrt {3}$)
B. (7,5)
C. ($5\sqrt {3}$,5)
D. ($5\sqrt {3}$,$3\sqrt {3}$)
答案:
A
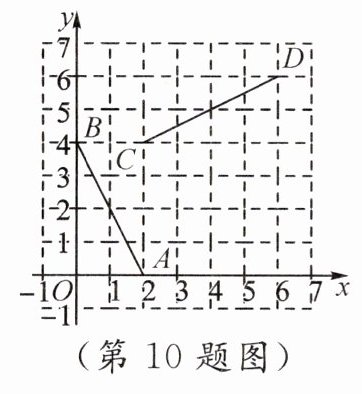
10. 如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为
(4,2)
.
答案:
(4,2)
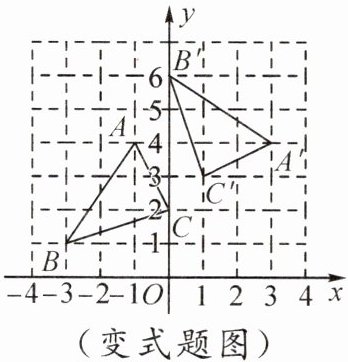
【变式】如图,在平面直角坐标系中,$△ABC$的顶点都在方格纸的格点上,将$△ABC$绕点P顺时针方向旋转$90^{\circ }$得到$△A'B'C'$,则点P的坐标为
(1,2)
.
答案:
(1,2)
11. (2024·广西柳州一模)如图,在平面直角坐标系xOy中,$△ABC$的三个顶点分别为A(-3,4),B(-5,1),C(-1,2).
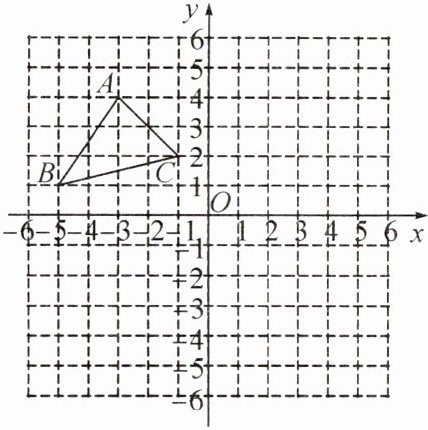
(1) 若$△A_{1}B_{1}C_{1}$与$△ABC$关于x轴对称,请写出点$A_{1},B_{1}$的坐标;
(2) 画出$△ABC$绕原点逆时针旋转$90^{\circ }$后的$△A_{2}B_{2}C_{2}$,并写出点$C_{2}$的坐标.

(1) 若$△A_{1}B_{1}C_{1}$与$△ABC$关于x轴对称,请写出点$A_{1},B_{1}$的坐标;
(2) 画出$△ABC$绕原点逆时针旋转$90^{\circ }$后的$△A_{2}B_{2}C_{2}$,并写出点$C_{2}$的坐标.
答案:
解:
(1)点A₁,B₁的坐标分别为(−3,−4),(−5,−1);
(2)如图,△A₂B₂C₂即为所求;点C₂的坐标为(−2,−1).

解:
(1)点A₁,B₁的坐标分别为(−3,−4),(−5,−1);
(2)如图,△A₂B₂C₂即为所求;点C₂的坐标为(−2,−1).

12. 在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把$△ABO$绕点B逆时针旋转,得到$△A'BO'$,点A,O旋转后的对应点为$A',O'$,记旋转角为α.
(1) 如图①,若$α=90^{\circ }$,求$AA'$的长;
(2) 如图②,若$α=120^{\circ }$,求点$O'$的坐标.
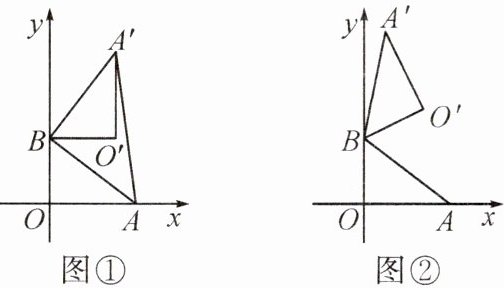
(1) 如图①,若$α=90^{\circ }$,求$AA'$的长;
$5\sqrt{2}$
(2) 如图②,若$α=120^{\circ }$,求点$O'$的坐标.
$(\frac{3\sqrt{3}}{2},\frac{9}{2})$

答案:
解:
(1)
∵点A(4,0),点B(0,3),
∴OA=4,OB=3,
∴AB= $\sqrt{OB^{2}+OA^{2}}$=$\sqrt{3^{2}+4^{2}}$=5.
∵△ABO绕点B逆时针旋转90°得△A'BO',
∴BA=BA',∠ABA'=90°,
∴△ABA'为等腰直角三角形,
∴AA'=$\sqrt{2}$BA=5$\sqrt{2}$;
(2)过点O'作O'H⊥y轴于点H.
∵△ABO绕点B逆时针旋转120°得△A'BO',
∴BO=BO'=3,∠OBO'=120°,
∴∠HBO'=180°−120°=60°,
∴∠BO'H=90°−60°=30°.在Rt△BHO'中,BH=$\frac{1}{2}$BO'=$\frac{3}{2}$,
∴O'H=$\sqrt{O'B^{2}-BH^{2}}$=$\sqrt{3^{2}-(\frac{3}{2})^{2}}$=$\frac{3\sqrt{3}}{2}$.又
∵OH=OB+BH=3 +$\frac{3}{2}$=$\frac{9}{2}$,
∴点O'的坐标为($\frac{3\sqrt{3}}{2}$,$\frac{9}{2}$).
(1)
∵点A(4,0),点B(0,3),
∴OA=4,OB=3,
∴AB= $\sqrt{OB^{2}+OA^{2}}$=$\sqrt{3^{2}+4^{2}}$=5.
∵△ABO绕点B逆时针旋转90°得△A'BO',
∴BA=BA',∠ABA'=90°,
∴△ABA'为等腰直角三角形,
∴AA'=$\sqrt{2}$BA=5$\sqrt{2}$;
(2)过点O'作O'H⊥y轴于点H.
∵△ABO绕点B逆时针旋转120°得△A'BO',
∴BO=BO'=3,∠OBO'=120°,
∴∠HBO'=180°−120°=60°,
∴∠BO'H=90°−60°=30°.在Rt△BHO'中,BH=$\frac{1}{2}$BO'=$\frac{3}{2}$,
∴O'H=$\sqrt{O'B^{2}-BH^{2}}$=$\sqrt{3^{2}-(\frac{3}{2})^{2}}$=$\frac{3\sqrt{3}}{2}$.又
∵OH=OB+BH=3 +$\frac{3}{2}$=$\frac{9}{2}$,
∴点O'的坐标为($\frac{3\sqrt{3}}{2}$,$\frac{9}{2}$).
查看更多完整答案,请扫码查看


