《2025年名师测控九年级数学上册人教版》

1. (原创题)下列现象中,不属于旋转现象的是 (B)
A. 钟摆的摆动
B. 电梯的上下移动
C. 方向盘的转动
D. 荡秋千的运动

答案： B

2. 将如图所示的图案以圆心为中心,旋转$180^{\circ }$后得到的图案是 (D)

答案： D

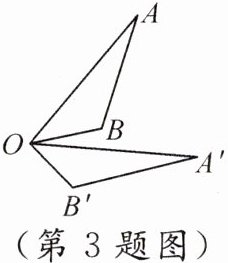
3. 如图,$△AOB$绕着点O旋转至$△A'OB'$,则:
(1)点B的对应点是点$B'$;
(2)旋转中心是点$O$,旋转角为$∠AOA'$或$∠BOB'$;
(3)$∠A$的对应角是$∠A'$,线段OB的对应线段是线段$OB'$.

答案：
(1)点$B'$
(2)点$O$ $∠AOA'$或$∠BOB'$
(3)$∠A'$ $OB'$

4. (2024·江苏无锡)如图,在$△ABC$中,$∠B=80^{\circ },∠C=65^{\circ }$,将$△ABC$绕点A逆时针旋转得到$△AB'C'$.当$AB'$落在AC上时,$∠BAC'$的度数为 (B)

A.$65^{\circ }$
B.$70^{\circ }$
C.$80^{\circ }$
D.$85^{\circ }$

答案： B

5. 如图,$△ABC$是等边三角形,D为BC边上的一点,$∠BAD=15^{\circ },△ABD$经过旋转到达$△ACE$的位置,那么$△ABD$至少旋转了$60^{\circ}$.

答案： $60^{\circ}$

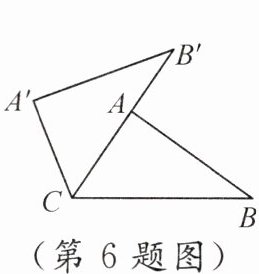
6. 如图,将$△ABC$绕点C逆时针旋转一定的角度得到$△A'B'C$,此时点A在边$B'C$上.若$BC=5,AC=3$,则$AB'$的长为2.

答案： 2

7. 如图,把一个直角三角尺ACB绕着$30^{\circ }$角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
(1)三角尺旋转了多少度?150°
(2)连接CD,判断$△CBD$的形状;△CBD是等腰三角形
(3)求$∠BDC$的度数.∠BDC=15°

答案： 解：
(1)$150^{\circ}$；
(2)$△CBD$是等腰三角形；
(3)$∠BDC=15^{\circ}$。

8. (2024·江西抚州一模)如图,在正方形ABCD中,$AB=4$,E为AB的中点,连接DE.将$△DAE$绕点D按逆时针方向旋转$90^{\circ }$得到$△DCF$,连接EF,求EF的长.

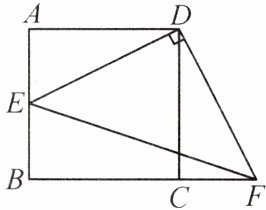
解：∵四边形$ABCD$是正方形，∴$AD=AB=4$，$∠A=90^{\circ}$。∵$E$为$AB$的中点，∴$EA=\frac{1}{2}AB=2$，∴$DE=\sqrt{EA^{2}+AD^{2}}=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$。又∵$△DAE$绕点$D$按逆时针方向旋转$90^{\circ}$得到$△DCF$，∴$DE=DF$，$∠EDF=90^{\circ}$，∴$EF=\sqrt{DE^{2}+DF^{2}}=\sqrt{2}DE=\sqrt{2}×2\sqrt{5}=$$2\sqrt{10}$。

答案： 解：
∵四边形$ABCD$是正方形，
∴$AD=AB=4$，$∠A=90^{\circ}$。
∵$E$为$AB$的中点，
∴$EA=\frac{1}{2}AB=2$，
∴$DE=\sqrt{EA^{2}+AD^{2}}=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$。又
∵$△DAE$绕点$D$按逆时针方向旋转$90^{\circ}$得到$△DCF$，
∴$DE=DF$，$∠EDF=90^{\circ}$，
∴$EF=\sqrt{DE^{2}+DF^{2}}=\sqrt{2}DE=\sqrt{2}×2\sqrt{5}=2\sqrt{10}$。