《2025年名师测控九年级数学上册人教版》

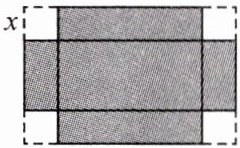
11. (教材$ P_{2} $“问题1”变式)如图是一块矩形铁皮,长50cm,宽30cm,在它的四个角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒,要制作的无盖方盒的底面积为$ 800cm^{2} $.设切去的正方形的边长为xcm,可列方程为(D)

A. $ 4x^{2}=800 $
B. $ 50×30-4x^{2}=800 $
C. $ (50-x)(30-x)=800 $
D. $ (50-2x)(30-2x)=800 $

答案： D

12. 若关于x的一元二次方程$ ax^{2}-bx-2025=0 $满足$ a+b=2025 $,则方程必有一根为(B)
A. 1
B. -1
C. ±1
D. 无法确定

答案： B

13. 若$ x=2n(n≠0) $是关于x的方程$ x^{2}-2mx+2n=0 $的根,则$ m-n $的值为$\frac {1}{2}$.

答案： $\frac {1}{2}$

14. 已知关于x的方程$ (k-3)x^{|k-1|}-5x=2 $.
(1)当k为何值时,方程是关于x的一元二次方程?
(2)若方程是关于x的一元一次方程,求k的值.

答案： 解:
(1)根据题意，得$|k-1|=2$，且$k-3≠0$，解得$k=-1$。
∴当$k=-1$时，方程是关于 x 的一元二次方程；
(2)当$k-3=0$时，解得$k=3$，此时方程为$-5x=2$，是一元一次方程；当$|k-1|=1$时，解得$k=0$，或$k=2$。方程分别为$-3x-5x=2$和$-x-5x=2$，都是一元一次方程。综上所述，当 k 的值为 3 或 0 或 2 时，方程是关于 x 的一元一次方程。

15. (教材$ P_{4} $习题$ T_{2} $变式)根据下列问题列出一元二次方程,并将其化成一般形式.
(1)两个连续奇数的平方和为130,求这两个奇数;
(2)一个QQ群里共有x个好友,每个好友都分别给群里其他好友发送一条消息,这样共有756条消息;
(3)小明用30cm的铁丝围成一个斜边长为13cm的直角三角形,求该直角三角形的两直角边长.

答案： 解:
(1)设 n 为任意整数，则两个连续奇数分别为$2n-1$，$2n+1$，则有$(2n-1)^{2}+(2n+1)^{2}=130$，$n^{2}-16=0$；
(2)$x(x-1)=756$，$x^{2}-x-756=0$；
(3)设该直角三角形的一直角边长为 a cm，则有$a^{2}+(17-a)^{2}=13^{2}$，$a^{2}-17a+60=0$。

16. 新视角 新定义将4个数a,b,c,d排成2行2列,两边各加一条竖线,记成$ \begin{vmatrix} a & b \\ c & d \end{vmatrix} $,定义$ \begin{vmatrix} a & b \\ c & d \end{vmatrix} =ad-bc $.上述记法就叫做二阶行列式.那么$ \begin{vmatrix} x+1 & x+2 \\ x-2 & 2x \end{vmatrix} =22 $表示的方程是一元二次方程吗?若是,请写出它的一般形式.
是，它的一般形式为$x^{2}+2x-18=0$

答案： 解: 根据题意，得$(x+1)\cdot 2x-(x+2)(x-2)=22$，$\therefore 2x^{2}+2x-x^{2}+4=22$，即$x^{2}+2x-18=0$，它符合一元二次方程的定义，是一元二次方程，其一般形式为$x^{2}+2x-18=0$。