第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
10. 已知关于$x$的一元二次方程$x^{2}-2mx + m^{2}+\frac{3}{2}m - 1 = 0$有两个实数根.
(1)求$m$的取值范围;
(2)设$x_{1}$,$x_{2}$是方程的两个实数根,当$m$取最大值时,求$x_{1}^{2}+x_{2}^{2}$的值.
(1)求$m$的取值范围;
(2)设$x_{1}$,$x_{2}$是方程的两个实数根,当$m$取最大值时,求$x_{1}^{2}+x_{2}^{2}$的值.
答案:
解:
(1) $\because$ 一元二次方程 $x^{2}-2mx + m^{2}+\frac{3}{2}m - 1 = 0$ 有两个实数根, $\therefore\Delta=b^{2}-4ac=(-2m)^{2}-4\times(m^{2}+\frac{3}{2}m - 1)=-6m + 4\geqslant0$, 解得 $m\leqslant\frac{2}{3}$. $\therefore$ 实数 $m$ 的取值范围为 $m\leqslant\frac{2}{3}$;
(2) $\because x_{1}+x_{2}=2m,x_{1}x_{2}=m^{2}+\frac{3}{2}m - 1$, $\therefore x_{1}^{2}+x_{2}^{2}=(x_{1}+x_{2})^{2}-2x_{1}x_{2}=(2m)^{2}-2(m^{2}+\frac{3}{2}m - 1)=2m^{2}-3m + 2$. 由
(1) 可知 $m\leqslant\frac{2}{3},\therefore m$ 的最大值为 $\frac{2}{3}$. 当 $m=\frac{2}{3}$ 时, $x_{1}^{2}+x_{2}^{2}=2\times(\frac{2}{3})^{2}-3\times\frac{2}{3}+2=\frac{8}{9},\therefore$ 当 $m$ 取最大值 $\frac{2}{3}$ 时, $x_{1}^{2}+x_{2}^{2}$ 的值是 $\frac{8}{9}$.
(1) $\because$ 一元二次方程 $x^{2}-2mx + m^{2}+\frac{3}{2}m - 1 = 0$ 有两个实数根, $\therefore\Delta=b^{2}-4ac=(-2m)^{2}-4\times(m^{2}+\frac{3}{2}m - 1)=-6m + 4\geqslant0$, 解得 $m\leqslant\frac{2}{3}$. $\therefore$ 实数 $m$ 的取值范围为 $m\leqslant\frac{2}{3}$;
(2) $\because x_{1}+x_{2}=2m,x_{1}x_{2}=m^{2}+\frac{3}{2}m - 1$, $\therefore x_{1}^{2}+x_{2}^{2}=(x_{1}+x_{2})^{2}-2x_{1}x_{2}=(2m)^{2}-2(m^{2}+\frac{3}{2}m - 1)=2m^{2}-3m + 2$. 由
(1) 可知 $m\leqslant\frac{2}{3},\therefore m$ 的最大值为 $\frac{2}{3}$. 当 $m=\frac{2}{3}$ 时, $x_{1}^{2}+x_{2}^{2}=2\times(\frac{2}{3})^{2}-3\times\frac{2}{3}+2=\frac{8}{9},\therefore$ 当 $m$ 取最大值 $\frac{2}{3}$ 时, $x_{1}^{2}+x_{2}^{2}$ 的值是 $\frac{8}{9}$.
11. 如图,一块长方形绿地的长为$100m$,宽为$50m$,在绿地中开辟两条道路后剩余绿地面积为$4704m^{2}$,则根据题意可列出方程(

A. $5000 - 150x = 4704$
B. $5000 - 150x - x^{2}=4704$
C. $5000 - 150x+\frac{1}{2}x^{2}=4704$
D. $(100 - x)(50 - x)=4704$
D
)
A. $5000 - 150x = 4704$
B. $5000 - 150x - x^{2}=4704$
C. $5000 - 150x+\frac{1}{2}x^{2}=4704$
D. $(100 - x)(50 - x)=4704$
答案:
D
12. (2024·四川绵阳)超市销售某种礼盒,该礼盒的原价为$500$元.因销量持续攀升,商家在$3$月份提价$20\%$,后发现销量锐减,于是经过核算决定在$3$月份售价的基础上,$4$,$5$月份按照相同的降价率$r$连续降价.已知$5$月份礼盒的售价为$486$元,则$r =$
$10\%$
.
答案:
$10\%$
13. (2024·广东汕头潮南区校级三模)综合与实践
【问题情景】学校综合实践小组进行废物再利用的环保小卫士行动,他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
【操作探究】
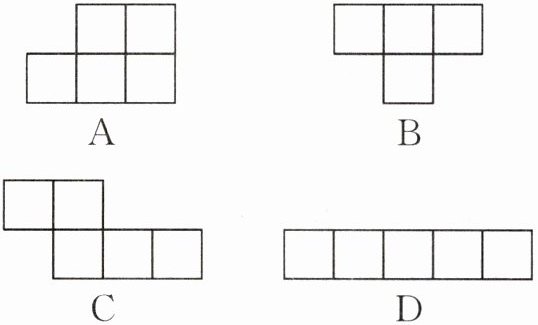
(1)若准备制作一个无盖的正方体纸盒,图中的______经过折叠能围成无盖正方体纸盒;
(2)如图①是小云的设计图,把它折成无盖正方体纸盒后与“保”字相对的字是“______”;

(3)如图②,有一张边长为$30cm$的正方形废弃宣传单,小张准备将其四角各剪去一个小正方形,折成无盖长方体纸盒.
①请你在图中画出示意图,用实线表示剪切线,虚线表示折痕;
②若要折成的无盖长方体纸盒底面积为$484cm^{2}$,求将要剪去的小正方形的边长,并求出这个纸盒的体积.
【问题情景】学校综合实践小组进行废物再利用的环保小卫士行动,他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
【操作探究】
(1)若准备制作一个无盖的正方体纸盒,图中的______经过折叠能围成无盖正方体纸盒;

(2)如图①是小云的设计图,把它折成无盖正方体纸盒后与“保”字相对的字是“______”;

(3)如图②,有一张边长为$30cm$的正方形废弃宣传单,小张准备将其四角各剪去一个小正方形,折成无盖长方体纸盒.
①请你在图中画出示意图,用实线表示剪切线,虚线表示折痕;
②若要折成的无盖长方体纸盒底面积为$484cm^{2}$,求将要剪去的小正方形的边长,并求出这个纸盒的体积.
答案:
解:
(1) C
(2) 卫
(3) ①所画出的图形如图所示;

②设将要剪去的小正方形的边长为 $x\mathrm{~cm}$. 根据题意, 得 $(30 - 2x)^{2}=484$. 解得 $x_{1}=4,x_{2}=26$ (不符合题意, 舍去), 此时纸盒的体积为 $4×484 = 1936(\mathrm{~cm}^{3})$. 答: 将要剪去的小正方形的边长为 $4\mathrm{~cm}$, 这个纸盒的体积为 $1936\mathrm{~cm}^{3}$.
解:
(1) C
(2) 卫
(3) ①所画出的图形如图所示;

②设将要剪去的小正方形的边长为 $x\mathrm{~cm}$. 根据题意, 得 $(30 - 2x)^{2}=484$. 解得 $x_{1}=4,x_{2}=26$ (不符合题意, 舍去), 此时纸盒的体积为 $4×484 = 1936(\mathrm{~cm}^{3})$. 答: 将要剪去的小正方形的边长为 $4\mathrm{~cm}$, 这个纸盒的体积为 $1936\mathrm{~cm}^{3}$.
查看更多完整答案,请扫码查看


