2025年细解巧练九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年细解巧练九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
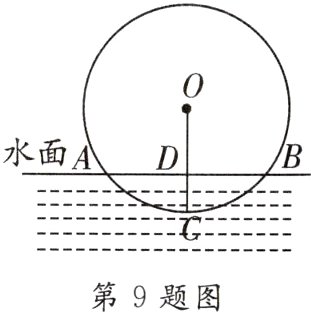
9. 唐代李皋发明了桨轮船,这种船是原始形态的轮船,是近代明轮航行模式之先导,如图,某桨轮船的轮子被水面截得的弦AB长为6 m,轮子的吃水深度CD为1.5 m,求该桨轮船的轮子直径.

答案:
解:如图,连接OB,设轮子的直径为d m,则其半径为$\frac{d}{2}$m.

由题意,得OC⊥AB,AD=BD=3m,
则在Rt△OBD中,OD²+BD²=OB²,
∴$(\frac{d}{2}-1.5)^{2}+3^{2}=(\frac{d}{2})^{2}$
解得d=7.5,
答:该桨轮船的轮子直径为7.5m.
解:如图,连接OB,设轮子的直径为d m,则其半径为$\frac{d}{2}$m.

由题意,得OC⊥AB,AD=BD=3m,
则在Rt△OBD中,OD²+BD²=OB²,
∴$(\frac{d}{2}-1.5)^{2}+3^{2}=(\frac{d}{2})^{2}$
解得d=7.5,
答:该桨轮船的轮子直径为7.5m.
10. 筒车是我国古代发明的一种水利灌溉工具. 如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理. 如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆. 已知圆心在水面上方,且圆被水面截得的弦AB长为6米,∠OAB = 41.3°,若点C为运行轨道的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin41.3°≈0.66,cos41.3°≈0.75,tan41.3°≈0.88)


答案:
解:如图,连接CO并延长,交AB于点D,
∵OD⊥AB,AB=6,
∴AD=$\frac{1}{2}$AB=3,
在Rt△OAD中,

∠OAB = 41.3°,
∴AO = $\frac{AD}{\cos41.3^{\circ}}\approx\frac{3}{0.75}$ = 4,OD = AD·tan41.3°≈3×0.88 = 2.64,
∴CD = OC + OD = AO + OD = 4 + 2.64 = 6.64,
答:点C到弦AB所在直线的距离是6.64米.
解:如图,连接CO并延长,交AB于点D,
∵OD⊥AB,AB=6,
∴AD=$\frac{1}{2}$AB=3,
在Rt△OAD中,

∠OAB = 41.3°,
∴AO = $\frac{AD}{\cos41.3^{\circ}}\approx\frac{3}{0.75}$ = 4,OD = AD·tan41.3°≈3×0.88 = 2.64,
∴CD = OC + OD = AO + OD = 4 + 2.64 = 6.64,
答:点C到弦AB所在直线的距离是6.64米.
11. 如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC = BE.
(1)求证:△CEB∽△CBD;
(2)若CE = 9,CB = 15,求DE的长;
(3)在(2)的条件下,求⊙O的直径.
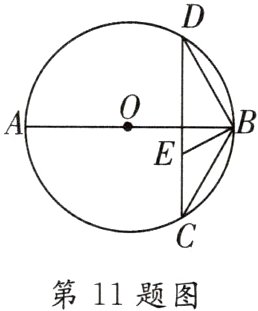
(1)求证:△CEB∽△CBD;
(2)若CE = 9,CB = 15,求DE的长;
(3)在(2)的条件下,求⊙O的直径.

答案:
解:
(1)证明:
∵弦CD垂直于直径AB,
∴$\overset{\frown}{BC}=\overset{\frown}{BD}$,
∴BC=BD,
∴∠C=∠D.
∵EC=BE,
∴∠C=∠CBE,
∴∠D=∠CBE.
又
∵∠C=∠C,
∴△CEB∽△CBD;
(2)
∵△CEB∽△CBD,
∴$\frac{CE}{CB}=\frac{CB}{CD}$.
∴CD = $\frac{CB^{2}}{CE}=\frac{15^{2}}{9}$ = 25,
∴DE=CD−CE=25−9=16;
(3)设弦CD与AB交于点H,圆的半径为r,连接OD,

∴CH=$\frac{1}{2}$CD=$\frac{25}{2}$,
BH = $\sqrt{15^{2}-(\frac{25}{2})^{2}}=\frac{5\sqrt{11}}{2}$,
在Rt△OHD中,OD² = OH² + DH²,则有
r² = $(r - \frac{5\sqrt{11}}{2})^{2}+(\frac{25}{2})^{2}$,
解得r = $\frac{45\sqrt{11}}{11}$.
所以⊙O的直径为$\frac{90\sqrt{11}}{11}$.
解:
(1)证明:
∵弦CD垂直于直径AB,
∴$\overset{\frown}{BC}=\overset{\frown}{BD}$,
∴BC=BD,
∴∠C=∠D.
∵EC=BE,
∴∠C=∠CBE,
∴∠D=∠CBE.
又
∵∠C=∠C,
∴△CEB∽△CBD;
(2)
∵△CEB∽△CBD,
∴$\frac{CE}{CB}=\frac{CB}{CD}$.
∴CD = $\frac{CB^{2}}{CE}=\frac{15^{2}}{9}$ = 25,
∴DE=CD−CE=25−9=16;
(3)设弦CD与AB交于点H,圆的半径为r,连接OD,

∴CH=$\frac{1}{2}$CD=$\frac{25}{2}$,
BH = $\sqrt{15^{2}-(\frac{25}{2})^{2}}=\frac{5\sqrt{11}}{2}$,
在Rt△OHD中,OD² = OH² + DH²,则有
r² = $(r - \frac{5\sqrt{11}}{2})^{2}+(\frac{25}{2})^{2}$,
解得r = $\frac{45\sqrt{11}}{11}$.
所以⊙O的直径为$\frac{90\sqrt{11}}{11}$.
12. 如图,在⊙O中,直径AB = 10,CD⊥AB于点E,CD = 8. 点F是弧BC上动点,且与点B,C不重合,P是直径AB上的动点,设m = PC + PF,则m的取值范围是( )
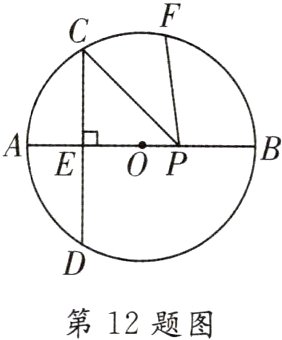
A. 8 < m≤4√5 B. 4√5 < m≤10
C. 8 < m≤10 D. 6 < m < 10

A. 8 < m≤4√5 B. 4√5 < m≤10
C. 8 < m≤10 D. 6 < m < 10
答案:
C
查看更多完整答案,请扫码查看


