《2025年细解巧练九年级数学下册北师大版》

11. [2024·龙沙区二模]如图，在抛物线 $y = x^{2}$ 的内部依次画正方形，使对角线在 $y$ 轴上，另两个顶点落在抛物线上. 按此规律类推，第 $2024$ 个正方形的边长是________.

答案： 2024√2

12. [2023·武汉三模]某家禽养殖场，用总长为 $200\ m$ 的围栏靠墙（墙长为 $65\ m$）围成如图所示的三块矩形区域，矩形 $EAGH$ 与矩形 $HGBF$ 面积相等，矩形 $EAGH$ 面积等于矩形 $DEFC$ 面积的二分之一，设 $AD$ 长为 $x\ m$，矩形区域 $ABCD$ 的面积为 $y\ m^{2}$.
（1）求 $y$ 关于 $x$ 的函数表达式，并写出自变量 $x$ 的取值范围；
（2）当 $x$ 为何值时，$y$ 有最大值？最大值是多少？
（3）现需要在矩形 $EAGH$ 和矩形 $DEFC$ 区域分别安装不同种类的养殖设备，单价分别为 $40$ 元/平方米和 $20$ 元/平方米，若要使安装成本不超过 $30000$ 元，请直接写出 $x$ 的取值范围.

答案：
解:
(1)由题意,得AE=DE=HG=BF=
CF=$\frac{1}{2}$xm,
DC=(200−$\frac{5}{2}$x{÷2=(100−$\frac{5}{4}$x)m,
∴y=AD.DC=(1000−$\frac{5}{4}$x)x
　　　=−$\frac{5}{4}$x²+100x.
　
∵0＜DC≤65,即0＜100−$\frac{5}{4}$r≤65,
　　解得28≤x＜80,
　
∴y=−$\frac{5}{4}$x²+100x(28≤x＜80);
(2)y=−$\frac{5}{4}$x²+100x
　　　　=−$\frac{5}{4}$(x−40)²+2000,
　
∵−$\frac{5}{4}$＜0,开口向下,对称轴为直线x=40,又
∵28≤x＜80,
　
∴当x=40时，y有最大值，y最夫为2000平方米;
(3)S矩形DEFC=CD.DE=$\frac{1}{2}$x.(10100−$\frac{5}{4}$x{=−$\frac{5}{8}$x²+50x,
　　S矩形EAGH=$\frac{1}{2}$S矩形DEFC=−$\frac{5}{16}$x²+25x,
　
∴(−$\frac{5}{8}$²+50x)×20+(−$\frac{5}{16}$x2+25xx)×40≤30000,
　　整理,得x²−80x+1200≥0.
　　设w=x²−80x+1200,令w=0，则x²−80x+1200=0,解得x1=20,x2=60,
　　如图，画出w关于x的函数图象.
　　　　　　　
由图可知,当x≤20或x≥60时,
　w=x²−80x+1200＞0.
　
∵28≤x＜80,
∴60≤x＜80.
　答:若要使安装成本不超过30000元，则x的取值范围为60≤x＜80.

13. [2023·榆林二模]如图，某动物园的大门由矩形 $ABCD$ 和抛物线形 $DMC$ 组成，以 $AB$，$AD$ 所在直线为 $x$ 轴，$y$ 轴建立平面直角坐标系，$AD=\frac{3}{4}\ m$，抛物线顶点 $M$ 的坐标为 $(\frac{9}{2},\frac{24}{5})$.
（1）求此抛物线对应的函数表达式；
（2）近期需对大门进行装修，工人师傅搭建一支撑杆方便施工，点 $P$ 正好在抛物线上且在点 $M$ 右侧，支撑杆 $PE\perp x$ 轴于点 $E$，$PE = 3$ 米，求支撑杆与大门最右侧的水平距离 $BE$.

答案： 解:
(1)根据题意，抛物线的顶点坐标为M($\frac{9}{2}$,$\frac{24}{5}$),且过D(o,$\frac{3}{4}$),
　设抛物线的表达式为y=α(x−$\frac{9}{2}$)²+$\frac{24}{5}$
　(a≠0),
　
∴(o−$\frac{9}{2}$)²a+$\frac{24}{5}$=$\frac{3}{4}$,解得α=一$\frac{1}{5}$,
∴抛物线的表达式为
　y=−$\frac{1}{5}$(x−$\frac{9}{2}$)²+$\frac{24}{5}$;
(2)由
(1)可知,抛物线的表达式为y=
　−$\frac{1}{5}$(x−−$\frac{9}{2}$)²+$\frac{24}{5}$,四边形ABCD是矩形,
∴点C的纵坐标为$\frac{3}{4}$,设点C的横坐标为xc,且抛物线的对称轴为直线r=$\frac{9}{2}$,
　
∴xC−$\frac{9}{2}$=$\frac{9}{2}$−0,解得xc=9,
　
∴点c(9,$\frac{3}{4}$),即AB=DC=9,
　且AD=BC=$\frac{3}{4}$.
　
∵点P正好在抛物线上且在点M右侧,支撑杆PE⊥x轴于点E,PE=3米,
　
∴设P(xp,3),且$\frac{9}{2}$＜xp＜9,
　
∴−$\frac{1}{5}$(xp−$\frac{9}{2}$)²²+$\frac{24}{5}$=3,
　解得xP1=$\frac{3}{2}$(舍去),xP2=$\frac{15}{2}$,
　
∴点E($\frac{15}{2}$,0),且B((9.0)).
　
∴BE=9−$\frac{15}{2}$=$\frac{3}{2}$,即支撑杆与大门最右侧的水平距离BE的长为$\frac{3}{2}$米.

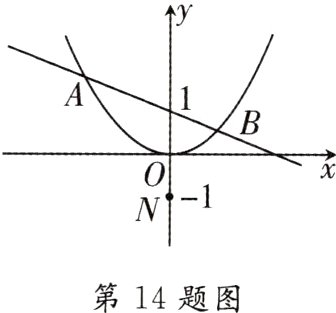
14. [逻辑推理][2023·巴中]在平面直角坐标系中，直线 $y = kx + 1$ 与抛物线 $y=\frac{1}{4}x^{2}$ 交于 $A$，$B$ 两点，设 $A(x_{1},y_{1})$，$B(x_{2},y_{2})$，则下列结论正确的个数为 （ ）
①$x_{1}\cdot x_{2}=-4$
②$y_{1}+y_{2}=4k^{2}+2$
③当线段 $AB$ 长取最小值时，则 $\triangle AOB$ 的面积为 $2$
④若点 $N(0,-1)$，则 $AN\perp BN$

A. $1$ 个
B. $2$ 个
C. $3$ 个
D. $4$ 个

答案： C