《2025年细解巧练九年级数学下册北师大版》

9.[2023·成都三模]科技创新是发展的第一动力，某科研公司向市场推出了一种新型电子产品，试销发现：该电子产品的销售价格y(元/件)与销售量x(件)之间满足一次函数关系，其图象如图所示，已知该产品的成本价是40元/件.
(1)求y关于x的函数表达式；
(2)求销售利润w(元)关于销售量x(件)的函数表达式，当销售量为多少时，销售利润最大？最大值是多少？

答案： 解:
(1)设销售价格y(元/件)与销售量x(件)
　之间的函数表达式为y=kx+b,
　由题意,得{6740==8500kk++bb,,
　解得k=−$\frac{1}{5}$
　　　　b=80,
　　　{
∴销售价格y(元/件)关于销售量x(件)的函数表达式为y=−$\frac{1}{5}$x+80;
(2)
∵w=(y−40)x,
∴w=(−$\frac{1}{5}$x+80−40)x=−$\frac{1}{5}$x²+40x
=−$\frac{1}{5}$(x−100)²+2000,
　答:当销售量为100件时，销售利润最大，最大值是2000元.

10.[2024·吉木萨尔县模拟]某农户在30天内采用线下店面和某电商平台带货两种方式销售一批农产品.其中一部分农产品在某电商平台带货销售，已知电商平台带货销售日销售量$y_{1}$(件)与时间x(天)关系如图所示.另一部分农产品在线下店铺销售，农产品的日销售量$y_{2}$(件)与时间x(天)之间满足函数关系$y_{2}=ax^{2}+bx$，其中部分对应值如表所示.

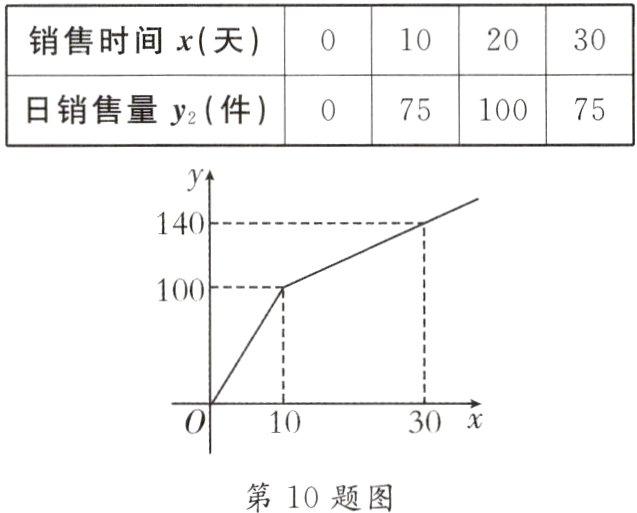
(1)写出$y_{1}$与x的函数关系式及自变量x的取值范围；
(2)试确定线下店铺日销售量$y_{2}$与x的函数关系式并求出线下店铺日销售量$y_{2}$的最大值；
(3)已知该农户线下销售该农产品每件利润为20元，在电商平台销售该农产品每件利润为30元，设该农户销售农产品的日销售总利润为w，写出w与时间x的函数关系式，并判断第几天日销售总利润w最大，并求出此时最大值.

答案： 解:
(1)当0≤x≤10,设y1=kx,
　将点(10,100)代入得100=10k,
　解得k=10,y1=10x,
　当x＞10时,设y1=k1x+b,将点(10,100),(30,140)代入得，{11104D=301k++bb,,
　解得{kb1==820,,
　
∴y1=2x+80,
　综上所述，y1={210xx+,08≤0,xx＞≤1100;,
(2)将(10,75),(20,100)代人y=ax²+bx,得{410000aa++2100bb==71500,,
　解得α=−$\frac{1}{4}$,
　　　　b=10,
　　　{
∴y2=−$\frac{1}{4}$x²+10x,
∵y2=−$\frac{1}{4}$x²+10x=−$\frac{1}{4}$(x−20)²+100,α=−$\frac{1}{4}$＜0,
∴当x=20时,y2的最大值为100;
(3)当0≤x≤10时,w=10x×30+(−$\frac{1}{4}$x²+10x{×20=300x−5x²+200x=−5x²+500x=−5(x−50)²+12500,
　对称轴为x=50,当x＜50时,w随x的增大而增大，
∵0≤x≤10,
∴当x=10时，取得最大值，最大值为
　−5×(10−50)²+12500=4500(元);
　当T＞10时，
　w=(22x+80)×30+(−$\frac{1}{4}$x²+10x)×20 =60x+2400−5x²+200x
　　=−5x²+260x+2400
　　=−5(x−26)²+5780,
∴当x=26时,w取得最大值，最大值为5780,
∴w={−−55xx²²++520600xx+,02≤4x0＜0,1x0＞,10,
　综上所述，第26天，日销售总利润w最大，最大值为5780元.