《2025年细解巧练九年级数学下册北师大版》

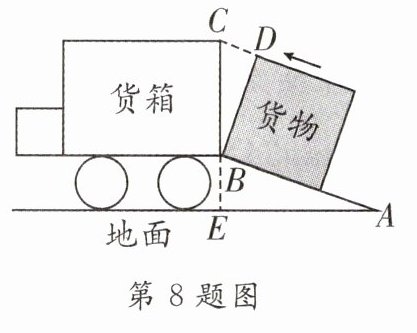
8.[2024·武汉]如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图，已知长方体货厢的高度BC为2米，斜坡AB的坡度i = $\frac{1}{3}$，现把图中的货物沿斜坡继续往前平移，当货物顶点D与C重合时，恰好可把货物放平装进货厢，则BD = ________.

答案： $\frac{3\sqrt{10}}{5}$米　解析:
∵沿斜坡继续往前平移，货物顶点D与C重合,
∴∠CDB=90°,
∵斜坡AB的坡度i=$\frac{1}{3}$,
∴tanA=$\frac{BE}{AE}$=$\frac{1}{3}$,
∵∠CBD+∠ABE=90°,∠ABE+∠A=
　90°,
∴∠CBD=∠A,
∴tan∠CBD=tanA=$\frac{CD}{BD}$=$\frac{BE}{AE}$=$\frac{1}{3}$
∴设CD=x米,则BD=3x米,
　在Rt△CBD中,CD²+BD²=BC²,
　即x²+(3x)²=2²,解得x=$\frac{\sqrt{10}}{5}$(负值舍去),
∴BD=$\frac{3\sqrt{10}}{5}$米.

9.[2024·武威二模]小明和小亮利用数学知识测量学校操场边升旗台上的旗杆高度.如图，旗杆AB立在水平的升旗台上，两人测得旗杆底端B到升旗台边沿C的距离BC = 2 m，升旗台的台阶所在的斜坡CD = 2 m，坡角(∠CDN)为30°，在太阳光下，小明测得旗杆的影子落在水平地面MN上的影长DE长为6 m，同一时刻，小亮测得长1.6 m的标杆直立于水平地面时的影子长为1.2 m.请你帮小明和小亮求出旗杆AB的高度.（结果保留根号）

答案：
解:延长AB交MN于点H,过点C作CG⊥MN于点G,
　　　　　
　则四边形BHGC是矩形,
∴HG=BC=2m,∠CGD=90°,BH=CG,
∵∠CDG=30°,CD=2m,
∴CG=$\frac{1}{2}$CD=1m,DG=$\sqrt{3}$m,
∴HE=HG+GD+DE=(8+$\sqrt{3}$)m,
∵同一时刻，物高和影长成正比，
∴$\frac{AH}{EH}$=$\frac{1.6}{1.2}$,
∴$\frac{AH}{8+\sqrt{3}}$=$\frac{1.6}{1.2}$,
∴AH=$\frac{4}{3}$(8+√3)m,
∴AB=AH−BH=$\frac{4}{3}$×(8+√3)−1
　　　　=$\frac{29 + 4\sqrt{3}}{3}$(m),
　答:旗杆AB的高度约为$\frac{29 + 4\sqrt{3}}{3}$m.

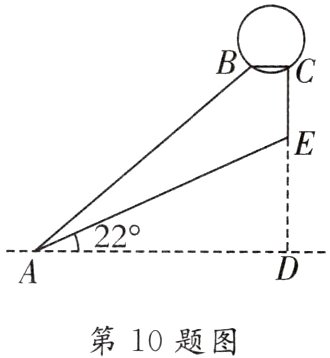
10.[2024·益阳二模改编]如图是安装在倾斜屋顶上的热水器的侧面示意图.已知屋面AE的倾斜角∠EAD为22°，长为3米的真空管AB的坡度为1 : $\frac{4}{3}$，安装热水器的铁架竖直管CE的长度为0.5米.
(1)求真空管上端B到水平线AD的距离；
(2)求安装热水器的铁架水平横管BC的长度.(结果精确到0.1米.参考数据：sin22°≈$\frac{3}{8}$，cos22°≈$\frac{15}{16}$，tan22°≈0.4)

答案：
解:
(1)如图,过点B作BF⊥AD于点F,在Rt△ABF中,BF:AF=1:$\frac{4}{3}$=3:4,
AB=3米,
设BF=3x米,则AF=4x米,
∴(3x)²+(4x)²=3²,
　解得x=0.6,
∴BF=3×0.6=1.8(米).
　答:真空管上端B到AD的距离约为1.8米;
(2)在Rt△ABF中,由
(1),得
AF=4x=4×0.6=2.4,
∵BF⊥AD,CD⊥AD,BC//FD,
∴四边形BFDC是矩形
∴BF=CD,BC=FD,
∵EC=0.5米,
∴DE=CD−CE=1.3米,
　在Rt△EAD中,∠EAD=22°,
　则AD=$\frac{DE}{\tan22°}$≈$\frac{1.3}{0.4}$=3.25(米),
∴BC=DF=AD−AF=3.25−2.4≈0.9(米),答:安装热水器的铁架水平横管BC的长度约为0.9米.

11.[2023·辽宁]暑假期间，小明与小亮相约到某旅游风景区登山.需要登顶600 m高的山峰，由山底A处先步行300 m到达B处，再由B处乘坐登山缆车到达山顶D处.已知点A，B，D，E，F在同一平面内，山坡AB的坡角为30°，缆车行驶路线BD与水平面的夹角为53°.（换乘登山缆车的时间忽略不计）
(1)求登山缆车上升的高度DE；
(2)若步行速度为30 m/min，登山缆车的速度为60 m/min，求从山底A处到达山顶D处大约需要多少分钟.(结果精确到0.1 min)（参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）

答案：
解:
(1)如图,过点B作
BM⊥AF于点M,由题
　意,　得∠A=　30°,
　∠DBE=53°,DF=600m,
　　　　　　　　　　　
AB=300m.
　在Rt△ABM中,
　∠A=30°,AB=300m,
　
∴BM=EF=$\frac{1}{2}$AB=150m,
　
∴DE=DF−EF=600−150=450(m),答:登山缆车上升的高度DE为450m;
(2)在Rt△BDE中,
　∠DBE=53°,DE=450m,
　
∴BD=$\frac{DE}{\sin53°}$≈$\frac{450}{0.80}$=562.5(m),
　
∴需要的时间t=t步行 + t车=$\frac{300}{30}$+$\frac{562.5}{60}$≈19.4(min),
　答:从山底A处到达山顶D处大约需要19.4分钟.