《2025年细解巧练九年级数学下册北师大版》

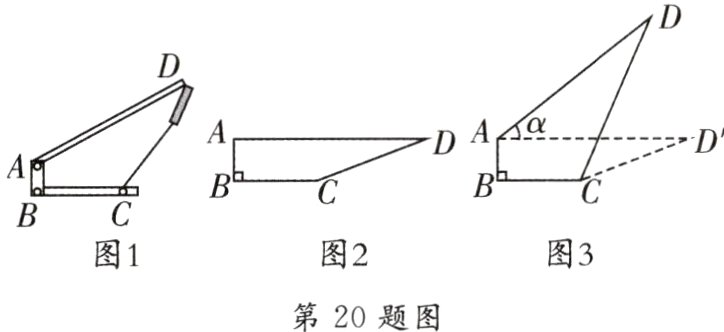
20. [2024·苏州]图1是某种可调节支撑架，BC为水平固定杆，竖直固定杆AB⊥BC，活动杆AD可绕点A旋转，CD为液压可伸缩支撑杆，已知AB = 10 cm，BC = 20 cm，AD = 50 cm.
（1）如图2，当活动杆AD处于水平状态时，求可伸缩支撑杆CD的长度（结果保留根号）；
（2）如图3，当活动杆AD绕点A由水平状态按逆时针方向旋转角度α，tanα = $\frac{3}{4}$且α为锐角，求此时可伸缩支撑杆CD的长度（结果保留根号）.

答案：
解:
(1)如图1,过点C作CE⊥AD,垂足为点E,
　　　　　　　
　　由题意可知∠B=∠A=90°,
　　又
∵CE⊥AD,
∴四边形ABCE为矩形
∵AB=10,BC=20,
　
∴AE=20,CE=10.
　
∵AD=50,
∴ED=30.在Rt△CED申,
CD=√CE²+ED²=　$\sqrt{10²+30²}$=10√10;即可伸缩支撑杆CD的长度为10$\sqrt{10}$cm;
(2)如图2,过点D作DF⊥BC,交BC的延长线于点F,交AD'于点G.
　　　　　　　
由题意可知四边形ABFG为矩形，
∴∠AGD=90°,
∵在Rt△AGD中,tana=$\frac{DG}{AG}$=$\frac{3}{4}$,
　
∴DG=$\frac{3}{4}$AG.
　
∴AD=√AG²+DG²=$\frac{5}{4}$AG,
　
∵AD=50,
∴AG=40,DG=30,
　
∴BF=AG=40,FG=AB=10,
　
∴CF=20,DF=40.
　在Rt△CFD中,
CD=　$\sqrt{CF²+DF2}$=　$\sqrt{20²+402}$=20√5.即可伸缩支撑杆CD的长度为20√5cm.

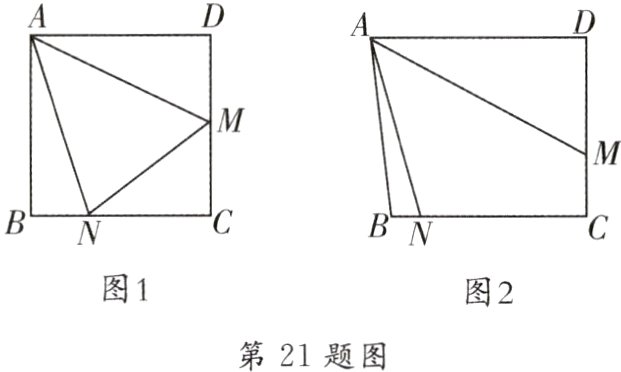
21. [2024·白云区一模]如图，在四边形ABCD中，点N，M分别在边BC，CD上. 连接AM，AN，MN，∠MAN = 45°.
（1）【实践探究】如图1，四边形ABCD是正方形.
（Ⅰ）若CN = 6，MN = 10，求∠CMN的余弦值；
（Ⅱ）若tan∠BAN = $\frac{1}{3}$，求证：M是CD的中点；
（2）【拓展】如图2，四边形ABCD是直角梯形，AD//BC，∠C = 90°，CD = 12，AD = 16，CN = 12，求DM的长.

答案：
解:
(1)(I)
∵四边形ABCD是正方形，
∴∠C=90°,
　
∴CM=　$\sqrt{MN²−CN2}$=　$\sqrt{102−62}$=8,
∴co√CMN=$\frac{CM}{MN}$=$\frac{8}{10}$=$\frac{4}{5}$;
　(II)证明:延长CB至点E,使BE=DM,连接AE,如图1,
　　　　　　
　
∵四边形ABCD是正方形,
　
∴AB=AD,∠ABE=∠D=90°,
　在△ABE和△ADM中,
AB=AD,
　　∠ABE=∠D,
BE=DM,
　{
　
∴△ABE≌△ADM(SAS),
　
∴AE=AM,∠EAB=∠DAM,
　
∵∠MAN=45°,
　
∴∠DAM+∠BAN=45°,
　
∴∠EAB+∠BAN=45°,
　
∴∠EAN=∠MAN,
　　在△EAN与△MAN中
　　　E=AM,
　EAN=∠MAN,
　　　N=AN,
　
∴△EAN≌△MAN(SAS),
　
∴EN=MN,
　设BN=m,DM=n,则MN=EN=m+n.
∵tan∠BAN=$\frac{1}{3}$=$\frac{BN}{AB}$,
　
∴AB=3m,
　
∴BC=CD=AB=3m,
　
∴CN=BC−BN=2m,CM=CD−DM=
　　3m−n.
　　在Rt△CMN中,
　
∵CN²+CN²=MN²,
　
∴(2m)²+(3m−n)²=(m+n)²,
　
∴3m=2n,
　
∴CM=3m−n=2n−n=n,
　
∵DM=n,
　
∴CM=DM,
　
∴M是CD的中点;
(2)以AD为边作正方形ADEF,延长AN,交EF于点G,延长EF至点H,使FH=
DM,连接AH,MG,延长CB交AF于点K,如图2,

　　　　　　　　第21题图
∵四边形ADEF为正方形,
∴AF=EF=DE=AD=16,
∵四边形ABCD是直角梯形,AD//BC,∠BCD=90°,
∴四边形AKCD为矩形,CN=12,CD=12,
∴CK=AD=16,AK=CD=12,
∴KN=CK−CN=16−12=4,
∵KN//EF,
∴△AKN∽△AFG,
∴$\frac{AK}{AF}$=$\frac{KN}{FG}$,
∴$\frac{12}{16}$=$\frac{4}{FG}$,
∴FG=$\frac{16}{3}$,
∴EG=EF−FG=$\frac{32}{3}$.
　在△AFH和△ADM中,
AF=AD,
　　∠AFH=∠D=90°,
　　FH=DM,
　{
∴△AFH≌△ADM(SAS),
∴AH=AM,
　同理
(1)得HG=MG.
　设DM=x,
　则EM=16−x,MG=HG=$\frac{16}{3}$+x,
∵EG²+EM²=MG²,
∴($\frac{32}{3}$)²+(16−x)²=($\frac{16}{3}$+x)²,
　解得x=8.
　
∴DM的长为8.

22. 直角三角形的两边长分别为6和8，则该直角三角形中最小角的余弦值为________.

答案： $\frac{4}{5}$或$\frac{3}{4}$