2025年细解巧练九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年细解巧练九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
8. [2024·大庆]如图,在平行四边形ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,且点E,F分别在边BC,AD上.
(1)求证:四边形AECF是平行四边形;
(2)若∠ADC = 60°,DF = 2AF = 2,求△GDF的面积.
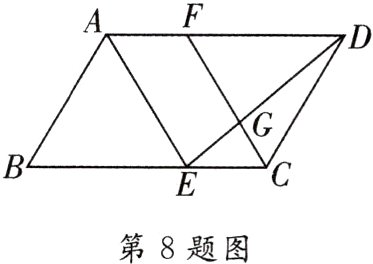
(1)求证:四边形AECF是平行四边形;
(2)若∠ADC = 60°,DF = 2AF = 2,求△GDF的面积.

答案:
解:
(1)证明:
∵四边形ABCD是平行四边形,
∴∠BAD = ∠BCD,AD//BC,
∵AE,CF分别是∠BAD,∠BCD的平分线,
∴∠BAE = ∠DAE = $\frac{1}{2}\angle BAD$,∠BCF = ∠DCF = $\frac{1}{2}\angle BCD$,
∴∠DAE = ∠BCF,
∵AD//BC,
∴∠DFC = ∠BCF,
∴∠DAE = ∠DFC,
∴AE//FC,
∴四边形AECF是平行四边形;
(2)由
(1)得∠DFC = ∠BCF,∠BCF = ∠DCF = $\frac{1}{2}\angle BCD$,
∴∠DFC = ∠DCF,
∴DF = DC,
∵∠ADC = 60°,
∴△DFC是等边三角形,
∴∠DFC = 60°,
∵DF = 2AF = 2,
∴DF = DC = CF = 2,CE = AF = 1,
∵AD//BC,
∴△DFG∽△ECG,
∴$\frac{FG}{CG}=\frac{DF}{CE}=\frac{2}{1}=2$,
∴FG = $\frac{2}{3}CF=\frac{4}{3}$,
作GH⊥DF于点H。

在Rt△FGH中,∠GFH = 60°,FG = $\frac{4}{3}$,
∴GH = FG·$\sin60^{\circ}=\frac{2}{3}\sqrt{3}$,
∴$S_{\triangle GDF}=\frac{1}{2}DF\cdot GH=\frac{1}{2}\times2\times\frac{2}{3}\sqrt{3}=\frac{2}{3}\sqrt{3}$。
解:
(1)证明:
∵四边形ABCD是平行四边形,
∴∠BAD = ∠BCD,AD//BC,
∵AE,CF分别是∠BAD,∠BCD的平分线,
∴∠BAE = ∠DAE = $\frac{1}{2}\angle BAD$,∠BCF = ∠DCF = $\frac{1}{2}\angle BCD$,
∴∠DAE = ∠BCF,
∵AD//BC,
∴∠DFC = ∠BCF,
∴∠DAE = ∠DFC,
∴AE//FC,
∴四边形AECF是平行四边形;
(2)由
(1)得∠DFC = ∠BCF,∠BCF = ∠DCF = $\frac{1}{2}\angle BCD$,
∴∠DFC = ∠DCF,
∴DF = DC,
∵∠ADC = 60°,
∴△DFC是等边三角形,
∴∠DFC = 60°,
∵DF = 2AF = 2,
∴DF = DC = CF = 2,CE = AF = 1,
∵AD//BC,
∴△DFG∽△ECG,
∴$\frac{FG}{CG}=\frac{DF}{CE}=\frac{2}{1}=2$,
∴FG = $\frac{2}{3}CF=\frac{4}{3}$,
作GH⊥DF于点H。

在Rt△FGH中,∠GFH = 60°,FG = $\frac{4}{3}$,
∴GH = FG·$\sin60^{\circ}=\frac{2}{3}\sqrt{3}$,
∴$S_{\triangle GDF}=\frac{1}{2}DF\cdot GH=\frac{1}{2}\times2\times\frac{2}{3}\sqrt{3}=\frac{2}{3}\sqrt{3}$。
9. [2024·随州模拟]如图1,在正方形ABCD中,AB = 5,M为对角线BD上的一点(不与点B,D重合),N为边AB上一点,连接CM,MN,且MN = CM.
(1)求证:MN⊥MC;
(2)若∠DCM = 30°,求$\frac{DM}{BM}$的值;
(3)如图2,连接NC交BD于点G,若$\frac{BG}{CG}=\frac{1}{3}$,求BN的长.

(1)求证:MN⊥MC;
(2)若∠DCM = 30°,求$\frac{DM}{BM}$的值;
(3)如图2,连接NC交BD于点G,若$\frac{BG}{CG}=\frac{1}{3}$,求BN的长.

答案:
解:
(1)证明:如图1,连接AM,
∵四边形ABCD是正方形,
∴MA = MC,∠MAN = ∠MCB,
∵MN = MC,
∴MA = MN,
∴∠MAN = ∠MNA,
∴∠MNA = ∠MCB,
∴∠MNA + ∠BNM = ∠MCB + ∠BNM = 180°,
∵∠ABC = 90°,
∴∠CMN = 90°,
即MN⊥MC;
(2)如图2,过点M作ME⊥CD于点E,MF⊥BC于点F,
∴四边形MFCE是矩形,
∴EC = MF,
∵∠CBD = ∠CDB = 45°,
设DE = ME = a,
则DM = $\sqrt{2}a$,
∵∠DCM = 30°,
∴CE = MF = $\sqrt{3}a$,
∴BM = $\sqrt{6}a$,
∴$\frac{DM}{BM}=\frac{\sqrt{2}a}{\sqrt{6}a}=\frac{\sqrt{3}}{3}$;
(3)由
(1)知△CMN是等腰直角三角形,
∴∠MCN = 45°,
又
∵∠ABD = 45°,
∴∠MCG = ∠NBG,
又
∵∠CGM = ∠BGN,
∴△BGN∽△CGM,
∴$\frac{BG}{CG}=\frac{BN}{CM}=\frac{1}{3}$,
设BN = x,则CM = MN = 3x,
∴CN = 3$\sqrt{2}x$,
∵BC = AB = 5,BN² + BC² = CN²,
∴x² + 5² = (3$\sqrt{2}x$)²,
∴x = $\frac{5\sqrt{17}}{17}$或 - $\frac{5\sqrt{17}}{17}$(舍去),
∴BN = $\frac{5\sqrt{17}}{17}$。


解:
(1)证明:如图1,连接AM,
∵四边形ABCD是正方形,
∴MA = MC,∠MAN = ∠MCB,
∵MN = MC,
∴MA = MN,
∴∠MAN = ∠MNA,
∴∠MNA = ∠MCB,
∴∠MNA + ∠BNM = ∠MCB + ∠BNM = 180°,
∵∠ABC = 90°,
∴∠CMN = 90°,
即MN⊥MC;
(2)如图2,过点M作ME⊥CD于点E,MF⊥BC于点F,
∴四边形MFCE是矩形,
∴EC = MF,
∵∠CBD = ∠CDB = 45°,
设DE = ME = a,
则DM = $\sqrt{2}a$,
∵∠DCM = 30°,
∴CE = MF = $\sqrt{3}a$,
∴BM = $\sqrt{6}a$,
∴$\frac{DM}{BM}=\frac{\sqrt{2}a}{\sqrt{6}a}=\frac{\sqrt{3}}{3}$;
(3)由
(1)知△CMN是等腰直角三角形,
∴∠MCN = 45°,
又
∵∠ABD = 45°,
∴∠MCG = ∠NBG,
又
∵∠CGM = ∠BGN,
∴△BGN∽△CGM,
∴$\frac{BG}{CG}=\frac{BN}{CM}=\frac{1}{3}$,
设BN = x,则CM = MN = 3x,
∴CN = 3$\sqrt{2}x$,
∵BC = AB = 5,BN² + BC² = CN²,
∴x² + 5² = (3$\sqrt{2}x$)²,
∴x = $\frac{5\sqrt{17}}{17}$或 - $\frac{5\sqrt{17}}{17}$(舍去),
∴BN = $\frac{5\sqrt{17}}{17}$。


10. [2023·广州三模]如图1,点D是边长为4的等边三角形ABC内部一点,满足BD = DC,且∠BDC = 120°,点E为BD延长线与边AC的交点.
(1)求DE的长;
(2)若△BDC绕点C顺时针旋转至△B'D'C处,如图2,点B的对应点为点B',点D的对应点为点D',连接AB'并取AB'的中点G,连接BG,D'G.
①试探究BG与D'G的关系,并说明理由;
②若将△BDC绕点C顺时针旋转一周,求线段BG的取值范围.
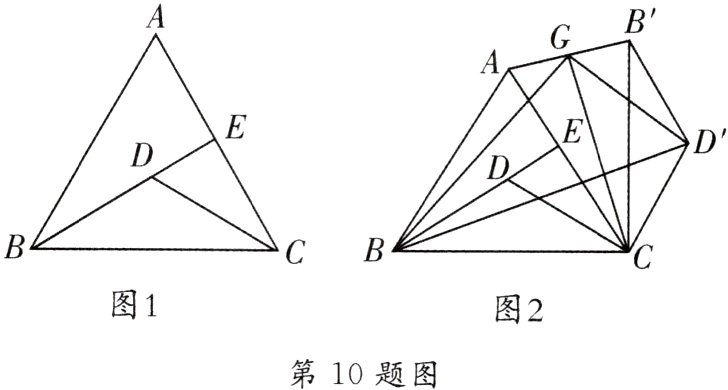
(1)求DE的长;
(2)若△BDC绕点C顺时针旋转至△B'D'C处,如图2,点B的对应点为点B',点D的对应点为点D',连接AB'并取AB'的中点G,连接BG,D'G.
①试探究BG与D'G的关系,并说明理由;
②若将△BDC绕点C顺时针旋转一周,求线段BG的取值范围.

答案:
解:
(1)
∵△ABC是等边三角形,
∴∠ABC = ∠ACB = 60°。
∵DB = DC,∠BDC = 120°,
∴∠DBC = ∠DCB = 30°,∠EDC = 60°,
∴∠ABD = ∠ACD = 30°,∠EBC + ∠ECB = 90°,
∴∠BEC = 90°,
∴DE = $\frac{1}{2}CD=\frac{1}{2}BD=\frac{1}{3}BE$。
∵BC = 4,
∴BE = BC·$\sin60^{\circ}=2\sqrt{3}$,
∴DE = $\frac{2\sqrt{3}}{3}$;
(2)①如图1中,结论BG⊥GD',BG = $\sqrt{3}GD'$。
理由:延长BG到点T,使得GT = GB,连接B'T,TD',延长BA,D'B',相交于点K。

∵AG = GB',∠AGB = ∠B'GT,BG = TG,
∴△AGB≌△B'GT(SAS),
∴AB = TB',∠ABG = ∠B'TG,
∴BK//TB',
∴∠K = ∠KB'T。
∵∠ABC = 60°,BC = AB,∠CD'B' = ∠CDB = 120°,
∴∠KBC + ∠CD'K = 180°,
∴∠K + ∠BCD' = 180°。
∵∠KB'T + ∠TB'D' = 180°,
∴∠BCD' = ∠TB'D'。
∵CD' = B'D',BC = B'C,
∴△BCD'≌△TB'D'(SAS),
∴D'B = D'T,∠CD'B = ∠TD'B',
∴∠BD'T = ∠CD'B' = 120°。
∵GB = GT,
∴D'G⊥BT,∠BD'G = ∠TD'G = 60°,
∴∠BGD' = 90°,
∴BG = GD'·$\tan\angle BD'G=\sqrt{3}GD'$,
∴BG⊥GD',BG = $\sqrt{3}GD'$;
②如图2中,连接GE。由题意,得AB = BC = AC = 4,∠ABC = 60°,
由
(1),得BE⊥AC,
∴AE = EC = 2,∠CBE = 30°,
BE = $\sqrt{3}EC = 2\sqrt{3}$。
∵AG = GB',AE = EC,
∴EG = $\frac{1}{2}CB' = 2$,
∴BE - EG≤BG≤BE + EG,
∴2$\sqrt{3}-2\leq BG\leq2\sqrt{3}+2$。

解:
(1)
∵△ABC是等边三角形,
∴∠ABC = ∠ACB = 60°。
∵DB = DC,∠BDC = 120°,
∴∠DBC = ∠DCB = 30°,∠EDC = 60°,
∴∠ABD = ∠ACD = 30°,∠EBC + ∠ECB = 90°,
∴∠BEC = 90°,
∴DE = $\frac{1}{2}CD=\frac{1}{2}BD=\frac{1}{3}BE$。
∵BC = 4,
∴BE = BC·$\sin60^{\circ}=2\sqrt{3}$,
∴DE = $\frac{2\sqrt{3}}{3}$;
(2)①如图1中,结论BG⊥GD',BG = $\sqrt{3}GD'$。
理由:延长BG到点T,使得GT = GB,连接B'T,TD',延长BA,D'B',相交于点K。

∵AG = GB',∠AGB = ∠B'GT,BG = TG,
∴△AGB≌△B'GT(SAS),
∴AB = TB',∠ABG = ∠B'TG,
∴BK//TB',
∴∠K = ∠KB'T。
∵∠ABC = 60°,BC = AB,∠CD'B' = ∠CDB = 120°,
∴∠KBC + ∠CD'K = 180°,
∴∠K + ∠BCD' = 180°。
∵∠KB'T + ∠TB'D' = 180°,
∴∠BCD' = ∠TB'D'。
∵CD' = B'D',BC = B'C,
∴△BCD'≌△TB'D'(SAS),
∴D'B = D'T,∠CD'B = ∠TD'B',
∴∠BD'T = ∠CD'B' = 120°。
∵GB = GT,
∴D'G⊥BT,∠BD'G = ∠TD'G = 60°,
∴∠BGD' = 90°,
∴BG = GD'·$\tan\angle BD'G=\sqrt{3}GD'$,
∴BG⊥GD',BG = $\sqrt{3}GD'$;
②如图2中,连接GE。由题意,得AB = BC = AC = 4,∠ABC = 60°,
由
(1),得BE⊥AC,
∴AE = EC = 2,∠CBE = 30°,
BE = $\sqrt{3}EC = 2\sqrt{3}$。
∵AG = GB',AE = EC,
∴EG = $\frac{1}{2}CB' = 2$,
∴BE - EG≤BG≤BE + EG,
∴2$\sqrt{3}-2\leq BG\leq2\sqrt{3}+2$。

查看更多完整答案,请扫码查看


