2025年细解巧练九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年细解巧练九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
7.[2023·宿州期中]如图,抛物线$y = ax^{2}+bx + 3$与$x$轴相交于点$A(1,0)$,$B(3,0)$,与$y$轴相交于点$C$。
(1)求抛物线的表达式;
(2)点$M(x_{1},y_{1})$,$N(x_{2},y_{2})$是抛物线上不同的两点且$x_{1}+x_{2}=6(x_{1}-x_{2})$,求$y_{1}-y_{2}$的最小值。
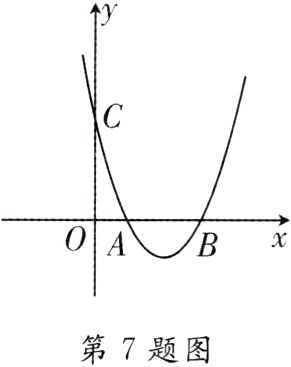
(1)求抛物线的表达式;
(2)点$M(x_{1},y_{1})$,$N(x_{2},y_{2})$是抛物线上不同的两点且$x_{1}+x_{2}=6(x_{1}-x_{2})$,求$y_{1}-y_{2}$的最小值。

答案:
解:
(1)设抛物线的表达式为$y = a(x - 1)(x - 3)=a(x^{2}-4x + 3)$,
∴$3a = 3$,解得$a = 1$,
故抛物线的表达式为$y = x^{2}-4x + 3$;
(2)由抛物线的表达式知,抛物线的对称轴为直线$x = 2$,
①若点$M$,$N$关于抛物线对称轴对称,
则$y_{1}=y_{2}$,
∴$y_{1}-y_{2}=0$;
②若点$M$,$N$不关于抛物线的对称轴对称时,$y_{1}-y_{2}=(x_{1}^{2}-4x_{1}+3)-(x_{2}^{2}-4x_{2}+3)=(x_{1}+x_{2})(x_{1}-x_{2})-4(x_{1}-x_{2})$,
∵$x_{1}+x_{2}=6(x_{1}-x_{2})$,
∴$y_{1}-y_{2}=(x_{1}+x_{2})(x_{1}-x_{2})-4(x_{1}-x_{2})$
$=6(x_{1}-x_{2})(x_{1}-x_{2})-4(x_{1}-x_{2})$
$=6(x_{1}-x_{2}-\frac{1}{3})^{2}-\frac{2}{3}$
当$x_{1}-x_{2}=\frac{1}{3}$时,$y_{1}-y_{2}$取得最小值,
即$y_{1}-y_{2}$的最小值为$-\frac{2}{3}$
(1)设抛物线的表达式为$y = a(x - 1)(x - 3)=a(x^{2}-4x + 3)$,
∴$3a = 3$,解得$a = 1$,
故抛物线的表达式为$y = x^{2}-4x + 3$;
(2)由抛物线的表达式知,抛物线的对称轴为直线$x = 2$,
①若点$M$,$N$关于抛物线对称轴对称,
则$y_{1}=y_{2}$,
∴$y_{1}-y_{2}=0$;
②若点$M$,$N$不关于抛物线的对称轴对称时,$y_{1}-y_{2}=(x_{1}^{2}-4x_{1}+3)-(x_{2}^{2}-4x_{2}+3)=(x_{1}+x_{2})(x_{1}-x_{2})-4(x_{1}-x_{2})$,
∵$x_{1}+x_{2}=6(x_{1}-x_{2})$,
∴$y_{1}-y_{2}=(x_{1}+x_{2})(x_{1}-x_{2})-4(x_{1}-x_{2})$
$=6(x_{1}-x_{2})(x_{1}-x_{2})-4(x_{1}-x_{2})$
$=6(x_{1}-x_{2}-\frac{1}{3})^{2}-\frac{2}{3}$
当$x_{1}-x_{2}=\frac{1}{3}$时,$y_{1}-y_{2}$取得最小值,
即$y_{1}-y_{2}$的最小值为$-\frac{2}{3}$
8.在平面直角坐标系中,抛物线$y = x^{2}-4x + 5$与$y$轴交于点$C$,则该抛物线关于点$C$成中心对称的抛物线的表达式为( )
A.$y=-x^{2}-4x + 5$
B.$y = x^{2}+4x + 5$
C.$y=-x^{2}+4x - 5$
D.$y=-x^{2}-4x - 5$
A.$y=-x^{2}-4x + 5$
B.$y = x^{2}+4x + 5$
C.$y=-x^{2}+4x - 5$
D.$y=-x^{2}-4x - 5$
答案:
A 解析:当$x = 0$时,$y = 5$,
∴$C(0,5)$;
设新抛物线上的点的坐标为$(x,y)$。
∵原抛物线与新抛物线关于点$C$成中心对称,由$2\times0 - x = -x$,$2\times5 - y = 10 - y$;
∴对应的原抛物线上点的坐标为$(-x,10 - y)$;代入原抛物线表达式可得$10 - y = (-x)^{2}-4\times(-x)+5$,
∴新抛物线的表达式为$y = -x^{2}-4x + 5$。
∴$C(0,5)$;
设新抛物线上的点的坐标为$(x,y)$。
∵原抛物线与新抛物线关于点$C$成中心对称,由$2\times0 - x = -x$,$2\times5 - y = 10 - y$;
∴对应的原抛物线上点的坐标为$(-x,10 - y)$;代入原抛物线表达式可得$10 - y = (-x)^{2}-4\times(-x)+5$,
∴新抛物线的表达式为$y = -x^{2}-4x + 5$。
9.[2023·宝坻期中]将抛物线$y=(x - 1)^{2}+2$沿$y$轴折叠后得到的新抛物线的表达式为( )
A.$y=(x + 1)^{2}-2$
B.$y=(x - 1)^{2}-2$
C.$y=-(x - 1)^{2}-2$
D.$y=(x + 1)^{2}+2$
A.$y=(x + 1)^{2}-2$
B.$y=(x - 1)^{2}-2$
C.$y=-(x - 1)^{2}-2$
D.$y=(x + 1)^{2}+2$
答案:
D
10.将抛物线$y = x^{2}+3$向上平移$1$个单位后,又沿$x$轴折叠,得新的抛物线,那么新的抛物线的表达式是__________。
答案:
$y = -x^{2}-4$
11.将抛物线$y=\frac{1}{2}(x + 2)^{2}+1$绕原点$O$旋转$180^{\circ}$,则得到的抛物线表达式为________。
答案:
$y = -\frac{1}{2}(x - 2)^{2}-1$
12.[2023·河源一模]抛物线$y = 2x^{2}-4x - 5$的图象先向左平移$3$个单位,再向上平移$4$个单位,再把抛物线绕顶点旋转$180^{\circ}$,得到的新图象的表达式为________。
答案:
$y = -2(x + 2)^{2}-3$
13.[2024·凉州区三模]如图,抛物线$C_{1}$的表达式为$y=-x^{2}+4$,将抛物线绕点$O$顺时针旋转$45^{\circ}$得到图形$G$,图形$G$分别与$y$轴,$x$轴正半轴交于点$A$,$B$,连接$AB$,则$\triangle OAB$的面积为________。


答案:
$-\sqrt{27}$
14.[2024·泰安]如图,抛物线$C_{1}:y = ax^{2}+\frac{4}{3}x - 4$的图象经过点$D(1,-1)$,与$x$轴交于点$A$,点$B$。
(1)求抛物线$C_{1}$的表达式;
(2)将抛物线$C_{1}$向右平移$1$个单位,再向上平移$3$个单位得到抛物线$C_{2}$,求抛物线$C_{2}$的表达式,并判断点$D$是否在抛物线$C_{2}$上;
(3)在$x$轴上方的抛物线$C_{2}$上,是否存在点$P$,使$\triangle PBD$是等腰直角三角形。若存在,请求出点$P$的坐标;若不存在,请说明理由。

(1)求抛物线$C_{1}$的表达式;
(2)将抛物线$C_{1}$向右平移$1$个单位,再向上平移$3$个单位得到抛物线$C_{2}$,求抛物线$C_{2}$的表达式,并判断点$D$是否在抛物线$C_{2}$上;
(3)在$x$轴上方的抛物线$C_{2}$上,是否存在点$P$,使$\triangle PBD$是等腰直角三角形。若存在,请求出点$P$的坐标;若不存在,请说明理由。

答案:
解:
(1)将点$D$的坐标代入抛物线表达式得$-1 = a+\frac{4}{3}-4$,
解得$a = \frac{5}{3}$,
则抛物线的表达式为$y = \frac{5}{3}x^{2}+\frac{4}{3}x - 4$;
(2)由题意得$C_{2}:y = \frac{5}{3}(x - 1)^{2}+\frac{4}{3}(x - 1)-4 + 3=\frac{5}{3}(x - \frac{3}{5})^{2}-\frac{19}{15}$,
当$x = 1$时,$y = \frac{5}{3}(x - \frac{3}{5})^{2}-\frac{19}{15}=\frac{5}{3}(1 - \frac{3}{5})^{2}-\frac{19}{15} = -1$,
故点$D$在抛物线$C_{2}$上;
(3)存在,理由:
令$y = \frac{5}{3}x^{2}+\frac{4}{3}x - 4 = 0$,解得$x_{1} = -2$,$x_{2} = \frac{6}{5}$,
∴点$B(-2,0)$。
当$\angle BDP$为直角时,
如图1,过点$D$作$DE\perp BD$且$DE = BD$,则$\triangle BDE$为等腰直角三角形,过点$D$作$y$轴的垂线$DG$,过点$B$,$E$分别作$DG$的垂线,垂足分别为点$G$,$H$,
∵$\angle BDG+\angle EDH = 90^{\circ}$,$\angle EDH+\angle DEH = 90^{\circ}$,
∴$\angle BDG = \angle DEH$,
∵$\angle DGB = \angle EHD = 90^{\circ}$,
∴$\triangle DGB\cong\triangle EHD(AAS)$,
则$DH = BG = 1$,$EH = GD = 1 + 2 = 3$,
则点$E(2,2)$,
当$x = 2$时,$y = \frac{5}{3}(x - \frac{3}{5})^{2}-\frac{19}{15}=\frac{5}{3}(2 - \frac{3}{5})^{2}-\frac{19}{15} = 2$,
即点$E$在抛物线$C_{2}$上,
即点$P$即为点$E(2,2)$;
当$\angle DBP$为直角时,如图2,过点$B$作$BE\perp BD$且$BE = BD$,则$\triangle BDE$为等腰直角三角形,过点$B$作$x$轴的垂线$BG$,过点$D$,$E$分别作$BG$的垂线,垂足分别为点$H$,$G$。
同理可得$\triangle BGE\cong\triangle DHB(AAS)$,
则$DH = 3 = BG$,$BH = 1 = GE$,
则点$E(-1,3)$,
当$x = -1$时,$y = \frac{5}{3}(x - \frac{3}{5})^{2}-\frac{19}{15}=\frac{5}{3}(-1 - \frac{3}{5})^{2}-\frac{19}{15} = 3$,
即点$E$在抛物线$C_{2}$上,
即点$P$即为点$E(-1,3)$;
当$\angle BPD$为直角时,
设点$E(x,y)$,
同理可得$\triangle EHB\cong\triangle DGE(AAS)$,
则$EH = x + 2 = GD = y + 1$且$BH = y = GE = 1 - x$,
解得$x = 0$且$y = 1$,即点$E(0,1)$,
当$x = 0$时,$y = \frac{5}{3}(x - \frac{3}{5})^{2}-\frac{19}{15}=\frac{5}{3}(0 - \frac{3}{5})^{2}-\frac{19}{15}\neq1$,
即点$E$不在抛物线$C_{2}$上;
综上所述,点$P$的坐标为$(2,2)$或$(-1,3)$。
(1)将点$D$的坐标代入抛物线表达式得$-1 = a+\frac{4}{3}-4$,
解得$a = \frac{5}{3}$,
则抛物线的表达式为$y = \frac{5}{3}x^{2}+\frac{4}{3}x - 4$;
(2)由题意得$C_{2}:y = \frac{5}{3}(x - 1)^{2}+\frac{4}{3}(x - 1)-4 + 3=\frac{5}{3}(x - \frac{3}{5})^{2}-\frac{19}{15}$,
当$x = 1$时,$y = \frac{5}{3}(x - \frac{3}{5})^{2}-\frac{19}{15}=\frac{5}{3}(1 - \frac{3}{5})^{2}-\frac{19}{15} = -1$,
故点$D$在抛物线$C_{2}$上;
(3)存在,理由:
令$y = \frac{5}{3}x^{2}+\frac{4}{3}x - 4 = 0$,解得$x_{1} = -2$,$x_{2} = \frac{6}{5}$,
∴点$B(-2,0)$。
当$\angle BDP$为直角时,
如图1,过点$D$作$DE\perp BD$且$DE = BD$,则$\triangle BDE$为等腰直角三角形,过点$D$作$y$轴的垂线$DG$,过点$B$,$E$分别作$DG$的垂线,垂足分别为点$G$,$H$,
∵$\angle BDG+\angle EDH = 90^{\circ}$,$\angle EDH+\angle DEH = 90^{\circ}$,
∴$\angle BDG = \angle DEH$,
∵$\angle DGB = \angle EHD = 90^{\circ}$,
∴$\triangle DGB\cong\triangle EHD(AAS)$,
则$DH = BG = 1$,$EH = GD = 1 + 2 = 3$,
则点$E(2,2)$,
当$x = 2$时,$y = \frac{5}{3}(x - \frac{3}{5})^{2}-\frac{19}{15}=\frac{5}{3}(2 - \frac{3}{5})^{2}-\frac{19}{15} = 2$,
即点$E$在抛物线$C_{2}$上,
即点$P$即为点$E(2,2)$;
当$\angle DBP$为直角时,如图2,过点$B$作$BE\perp BD$且$BE = BD$,则$\triangle BDE$为等腰直角三角形,过点$B$作$x$轴的垂线$BG$,过点$D$,$E$分别作$BG$的垂线,垂足分别为点$H$,$G$。
同理可得$\triangle BGE\cong\triangle DHB(AAS)$,
则$DH = 3 = BG$,$BH = 1 = GE$,
则点$E(-1,3)$,
当$x = -1$时,$y = \frac{5}{3}(x - \frac{3}{5})^{2}-\frac{19}{15}=\frac{5}{3}(-1 - \frac{3}{5})^{2}-\frac{19}{15} = 3$,
即点$E$在抛物线$C_{2}$上,
即点$P$即为点$E(-1,3)$;
当$\angle BPD$为直角时,
设点$E(x,y)$,
同理可得$\triangle EHB\cong\triangle DGE(AAS)$,
则$EH = x + 2 = GD = y + 1$且$BH = y = GE = 1 - x$,
解得$x = 0$且$y = 1$,即点$E(0,1)$,
当$x = 0$时,$y = \frac{5}{3}(x - \frac{3}{5})^{2}-\frac{19}{15}=\frac{5}{3}(0 - \frac{3}{5})^{2}-\frac{19}{15}\neq1$,
即点$E$不在抛物线$C_{2}$上;
综上所述,点$P$的坐标为$(2,2)$或$(-1,3)$。
查看更多完整答案,请扫码查看


